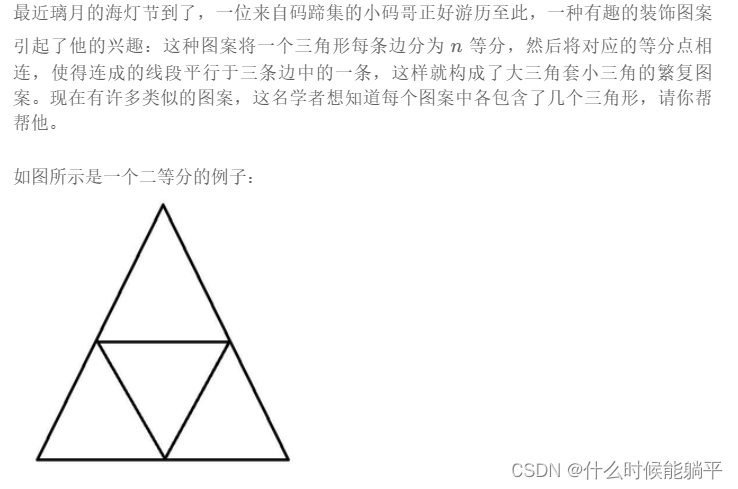
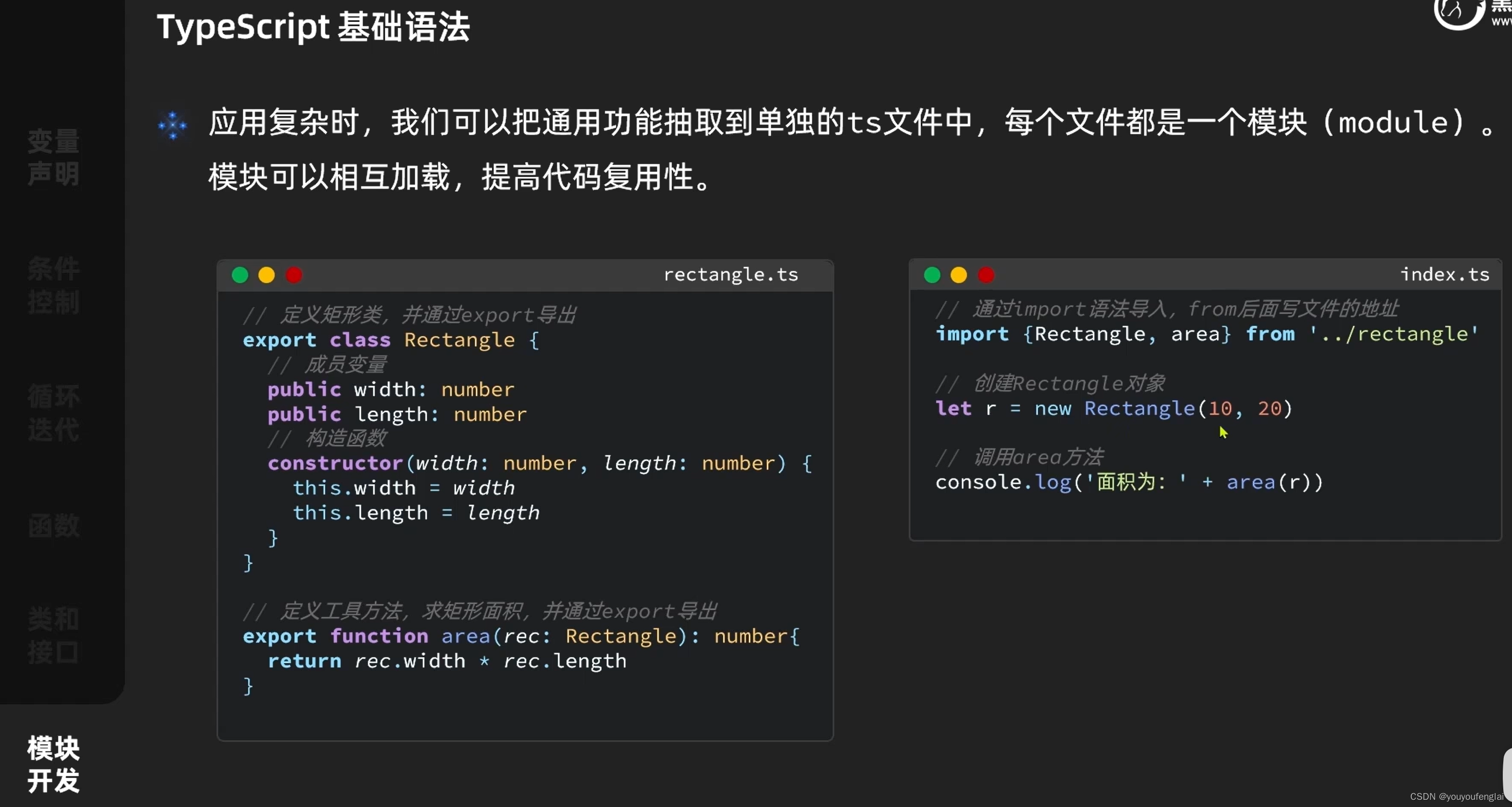
思路：找规律，推公式

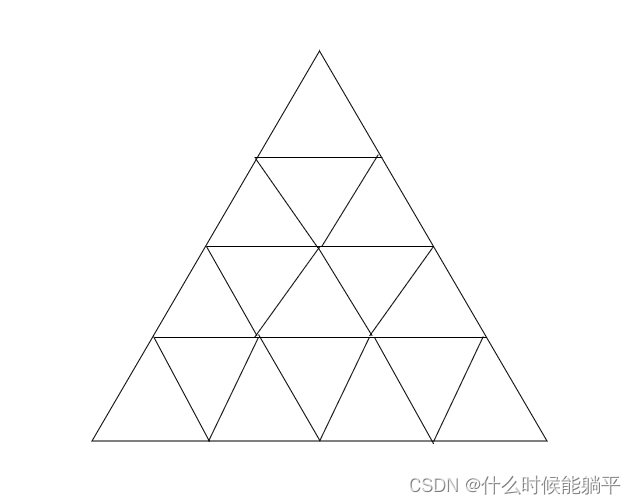
4等分：

        头朝上的三角形：

                边长为1：1+2+3+4=s1；

                边长为2：1+2+3=s2；

                边长为3：1+2=s3；

                边长为4：1=s4；

        即si=1+2+...+n-i+1=(n-i+2)*(n-i+1)/2

同理：头朝下的三角形：

                n=1：s=0；(1层)

                n=2：s=0+1；(2层)

                n=3：s=0+(1+2)；(3层)

                n=4：s=0+1+(1+2+3)；(4层)

                n=5：s=0+(1+2)+(1+2+3+4)；

                n=6：s=0+1+(1+2+3)+(1+2+3+4+5)；

        即f(n)=f(n-2)+(1+2+...+n-1)=f(n-2)+n*(n-1)/2

#include <bits/stdc++.h>
using namespace std;
int n;
int f(int n)
{
    if (n == 1)
        return 0;
    if (n == 2)
        return 1;
    return f(n - 2) + n * (n - 1) / 2;
}
int main()
{
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        int x;
        cin >> x;
        int sum0 = 0, sum1 = 0; // 记录头朝上和头朝下的三角形数
        for (int j = 1; j <= x; j++)
        {

            sum0 += (x - j + 1) * (x - j + 2) / 2; // 头朝上
        }
        sum1 = f(x); // 头朝下
        cout << sum0 + sum1 << endl;
    }
    return 0;
}