第六讲-流程挖掘（Process Mining）学习日志之α算法精讲

通过给定一个简单的事件日志，α算法可以得到一个(希望)能够重演日志的 Petri 网。同时α算法是最早的能够适当处理并发的过程发现算法之一。

---

参考：PROCESS MINING：Discovery,Conformance and Enhancement of Business Processes

---

6.1 基本思想

注：约定大写字母表示活动的集合，小写字母表示某个具体活动(例如a,b,c,…∈.b) 。

α算法的输入：一个基于集合 A 的简单事件日志 L，即L∈B(A) 。为了方便记忆， 我们简单的用 L 表示事件日志。集合 A 中的元素是活动 (activities)，这些活动对应着得到的 Petri 网中的变迁。

α算法的输出：带初始标识的 Petri 网，即 α(L)=(N,M)。因为我们的目标是找到一个工作流网，所以可以省略初始标识 (initial marking)，记为 a(L)=N (初始标识默认为 M=[i] )。

---

α算法扫描事件日志，从而找出特定的模式。举例来说，如果活动 b 紧跟在活动 a 之 后，但是活动 a 从不出现在活动 b 的后面，那么可以认为 a 和 b 之间存在因果依赖关系。为了反映这一关系，对应的 Petri 网中应该有一个连接 a 和 b 的库所。为了捕捉日志中的相关模式，我们需要区分4种基于日志的次序关系(ordering relations)。

基于日志的次序关系

使用 L 表示一个基于 A 的事件日志，即 L∈B(A)。令a,b, ∈ A，那么：

• a>_Lb 当且仅当存在一个轨迹 σ=<t₁,t₂,t₃,…,t_n>，i∈{1,…,n-1} 使得 σ∈L，t_i=a 并且 t_i+1=b；
• a→ _Lb 当且仅当 a>_Lb 并且 b≯_La；
• a#_Lb 当且仅当 a≯_Lb 并且 b≯_La；
• all_Lb 当且仅当 a>_Lb 并且 b>_La；

再次考虑 L₁=[<a,b,c,d>³,<a,c,b,d>²,<a,e,d>]，在这个事件日志中，可以找到如下基于日志的次序关系：

1）>_L₁={(a,b),(a,c),(a,e),(b,c),(c,b),(b,d),(c,d),(e,d)}
2）→_L₁={(a,b),(a,c),(a,e),(b,d),(c,d),(e,d)}
3）#_L₁={(a,a),(a,d),(b,b),(b,e),(c,c),(c,e),(d,a),(d,d),(e,b),(e,c),(e,e)}
4）ll_L₁={(b,c),(c,d)}

其中 >_L₁ 关系包含了所有紧邻的活动对，例如在轨迹 <a,b,c,d> 中 d 紧跟在 c 之后，所以有 c>_L₁d。 但是 d≯_L₁c, 因为在日志的任何轨迹中都不存在 c 紧跟 d 之后的情况。→_L₁ 包含了全部具有因果关系的活动对，例如 c→_L₁d，因为有时 d 紧跟在 c 之后，反之则不然 (c>_L₁d 且 d≯_L₁c)。bll_L₁c 因为 b>_L₁c 并且 c>_L₁b，也就是说，有时 c 紧跟在 b 之后，有时则反过来。b#_L₁e 因为 b≯_L₁e 并且 e≯_L₁b。

对于任意基于的 A 日志 L 以及 x,y∈A，一定有x→_Ly，y→_Lx，x#_Ly 或者 xll_Ly，也就是说，任一活动对一定满足这4种关系中的一种。因此，可以使用一个矩阵来描述日志的足迹 (footprint)，如表5.1所示。
表 5.2 展示了日志 L₂ 的足迹，为了使表格不显得混乱，省略了下标。比较日志 L₁ 和 L₂ 的足迹，可以发现只有 e 和 f 的行和列有所不同。

如图 5.4 所示，基于日志的顺序关系可以用于发现相应的过程模型中的模式。如果 a 和 b 之间有先后次序，那么日志会显示 a→_L₁b。 如果 a 发生后需要在 b 和 c 之间做出选择，那么日志会显示a→_L₁b，a→_L₁c 和 b#_L₁c，因为 b 和 c 紧跟 a 之后，而 b 和 c 二者互不相邻。这一模式被称为 XOR-split，与之对应的是 XOR-join 模式，如图 5.4 (b-c) 所示。如果 a→_Lc，b→_Lc 并且有a#_L₁b，那么就意味着 a 或 b 发生之后，c 应该发生。AND-split 模式，和它对应的是 AND-join 模式，如图 5.4 (d~e) 所示。如果 a→_Lb，b→_Lc 并且有 bll_Lc，就表示当 a 发生之后，b 和 c 可以并行发生 (AND-split 模式)。如果a→_Lc，b→_Lc 并且有 all_Lb, 日志就暗示我们 c 发生之前必须先同步 a 和 b (AND-join 模式)。

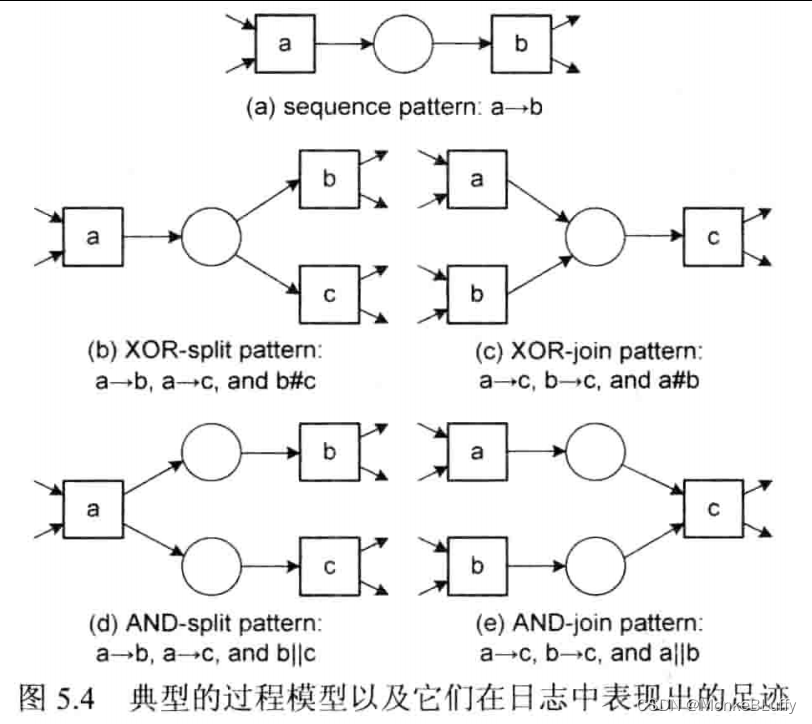
图 5.4 仅仅展示了几种简单的模式，并没有说明推导出这些模式所需的附加条件，但是这幅图很好地阐释了我们的基本思想。

举例

举例来说，考虑图5.5中的工作流网 N₃ 和事件日志L₃，它描述了4个实例。

L₃=[<a,b,c,d,e,f,b,d,c,e,g>,<a,b,d,c,e,g>²,<a,b,c,d,e,f,b,c,d,e,f,b,d,c,e,g>]

α算法基于 L₃ 构建出了工作流网 N₃ (如图5.5所示)。

表5.3展示了 L₃ 的足迹，注意模型中的模式确实与从事件日志中提取出的次序关系相符。例如，考虑由 b、c、d 和 e 组成的过程片段，显然这一片段可以基于 b→_L₃c、b→_L₃d、cll_L₃d、c→_L₃e 和 d→_L₃e 这些关系构建出来。而 e 后的选择结构则由 e→_L₃f、e→_L₃g 和 fll_L₃g 得到。

图5.6展示了另一个例子，由日志 L₄ 可以得到工作流网N₄。

L₄=[<a,c,d>4⁵,<b,c,d>4²,<a,c,e>³8,<b,c,e>²]

L₄包含了147个案例的信息，这些案例遵循4个轨迹。观察每个轨迹的第一个和最后 一个活动，可以很容易地发现有两个开始活动和两个结束活动。

6.2 α算法

令 L 表示一个基于 T⊆A 的事件日志，那么 α(L) 的定义如下：

L 是一个基于某个活动集合 T 的事件日志。在第一步中，检查哪些活动出现在日志中 (T_L)， 这些活动对应着最终生成的工作流网中的变迁。T_I 是开始活动的集合，即在轨迹中出现在第一个位置的所有活动的集合(第二步)。To 是结束活动的集合，即在轨迹中出现在最后一个位置的所有活动的集合(第三步)。第四步和第五步是 α 算法的核心。现在面临的挑战是确定工作流网的库所以及它们之间的连接关系，我们的目标是构建名为 p_(A,B) 的库所，此处 A 是 p_(A,B) 的输入变迁集合 (·p_(A,E)=A) 并且 B 是 ·p_(A,B) 的输出变迁集合 (p_(A,B)·=B)。

图5.7展示了寻找 p_(A,B) 的基本动机。集合 A 中的所有元素都与集合 B 中的所有元素有因果关系，也就是说，对于所有(a,b)∈A×B，有 a→_Lb 。此外，集合 A 中的元素不会出现一个跟在另 一个后面的情况，即对于所有a₁，a₂，∈A 都有a₁#La₂，这一要求对于集合 B 中的元素也是一样。
表5.4 展示了我们之前介绍的足迹矩阵。如果我们只考虑对应着 AUB 的行和列并且将这些行列分别组织起来，就能够得到如表5.4所示的模式。表的内容可以划分为4个部 分，其中两个部分只包含符号#,这表示 A 中的任何一个元素不能紧跟 A 中的另一个元素 (左上部分)，同样 B 中的任何一个元素也不能紧跟 B 中的另一个元素(右下部分)。右上部分只包含符号→，这意味着 B 中的任何一个元素可以紧跟 A 中的任何一个元素，反之则不然。与之相对称，可以看到表的左下部分只包含符号←。
让我们再次考虑日志L₁，很明显，A={a} 和 B={b,e} 满足第四步的要求。同样地，A’={a} 和 B’={b} 也满足相同的要求。所有满足上述要求的 A，B 对构成的集合就是 X_L 。在日志L₁的情况下：

X_L1={({a},{b}),({a},{c}),({a},{e}),({a},{b,e}),({a},{c,e}),({b},{d}),({c},{d}), ({e},{d}),({b,e},{d}),({c,e},{d})}

如果把X₁中的每一个元素都作为一个库所，会导致库所过多。因此，应该只包含“最大的”(A,B) 。 注意到对于任一对(A,B)∈X_L、非空集合 A⊆A’和非空集合 B⊆B’, 都有(A’,B’)∈X_L。在算法的第五步中，所有不是最大的集合都被移除，得到：

Y={({a},{b,e}),({a},{c,e}),({b,e},{d}),({c,e},{d})}

同样可以使用足迹矩阵来理解第五步。考虑表5.4，令φ⊂A⊆A’且φ⊂B⊆B’, 移除行和列AUB(A’UB‘) 得到的矩阵仍然保持着表5.4中的模式。因此，我们只考虑构建Y_L的最大矩阵。

每一个元素(A,B)∈Y_L都对应着一个库所p_(A,B)，这个库所连接了A和B中的变迁。另外，p_L也包含一个唯一的源库所i_L和一个唯一的汇结库所 o_L (第六步)。记住我们的目标是构造一个工作流网。

第七步生成工作流网的弧。T_I中的所有变迁都以i_L作为输入库所，To中的所有变迁都以o_L作为输出库所。所有库所p_(A,B)都以 A 作为输入结点，以B作为输出结点。最终得到的结果是一个Petri网α(L)=(P_L,T_L,F_t)，它描述了事件日志L所反映出来的行为。

至此，我们展示了4个日志和4个工作流网。应用α算法可以得到a(L₃)=N₃，a(L₄)=N₄。在图5.5和图5.6中，库所分别基于集合Y_L3 和Y_L4命名。此外，通过重命名库所可以知道α(L₁)=N₁，α(L₂)=N₂ (图5.1和图5.2中使用了不同的库所名)。这些例子说明α算法确实能够基于事件日志发现工作流网。

现在让我们考虑事件日志L5:

Ls=[<a,b,e,f>²,<a,b,e,c,d,b,f>³,<a,b,c,e,d,b,f>²,<a,b,c,d,e,b,f>⁴,<a,e,b,c,d,b,f>³]

表5.5展示了这一日志的足迹。
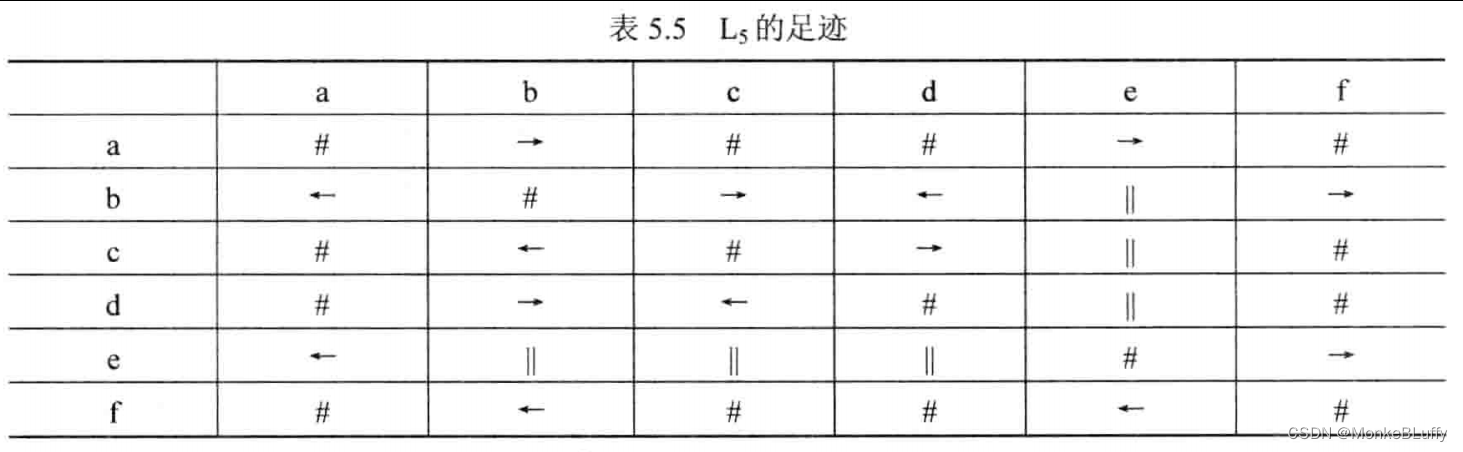让我们将α算法的8个步骤应用到L=L5上。
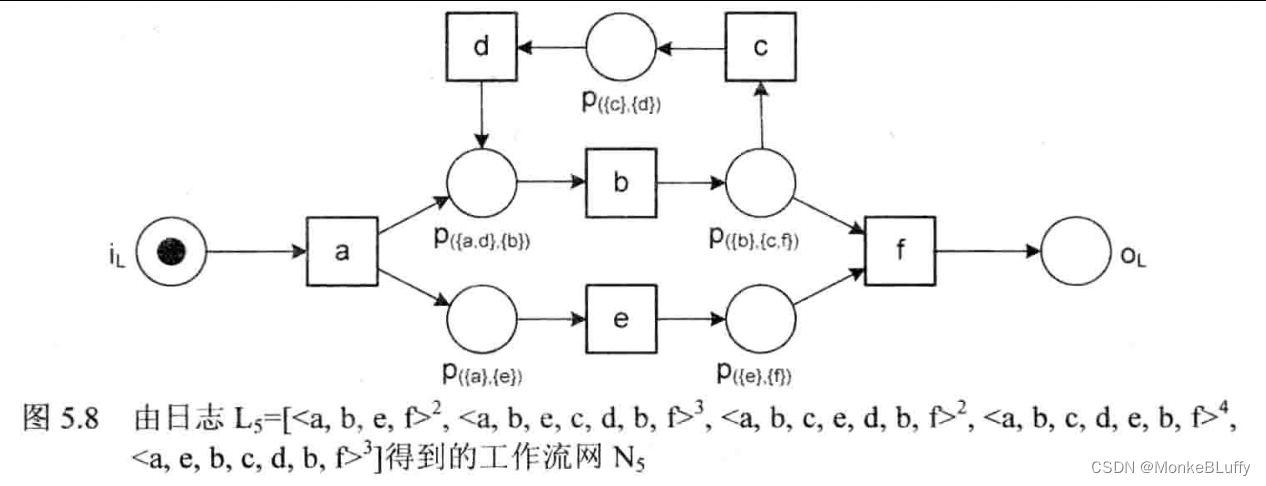
图5.8展示了N₅=α(L₅)，即我们刚刚计算出来的模型。N₅可以重演L₅中的所有轨迹。因为可以由一个库所周围的变迁来推出它的名称，所以为了避免图变得混乱，图5.8中并没有给出库所名，在之后的工作流网中也不会给出。

6.3 α算法中的不足

α算法能够发现一大类工作流网，前提是日志 L 针对基于日志的次序关系>_L是完备的(complete) 。这一假设意味着对于任一完备的事件日志L, 如果 b 紧跟 a，那么就有a>_Lb。因此，例如表5.5中的足迹被认为是合法的。在本章的后面我们会再次讨论完备性这一概念。

即使我们假设日志是完备的，a 算法还是存在一些问题。有许多不同的工作流网拥有相同的行为，也就是说，两个模型可能在结构上不同但是具有等价的轨迹。例如下面这个事件日志：

L₆=[<a,c,e,g>²,<a,e,c,g>³,<b,d,f,g>²,<b,f,d,g>]

图5.9展示了α(L₆)，尽管这一模型能够产生日志中的行为，但是得到的工作流网却不必要地复杂了许多。g的两个输入库所是冗余的，可以移除它们同时不改变行为。库所 p₁ 和 p₂ 被称为隐式库所 (implicit places)，可以在移除隐式库所的同时不对可能的发生序列造成影响。事实上，图5.9仅仅展示了许多轨迹等价的工作流网中的一个。

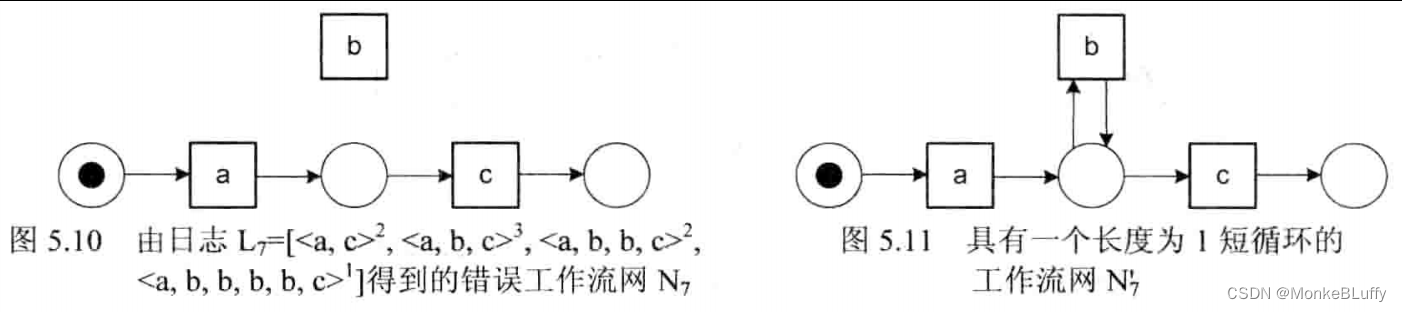
原始的α算法(参考5.2.2节)在处理短循环，即长为1或2的循环时存在问题。先看看长度为1的循环，图5.10展示了工作流网 N₇, 它是将基本的α算法应用到日志 L₇ 上得到的结果。

L₇=[<a,c>²,<a,b,c>³,<a,b,b,c>²,<a,b,b,b,b,c>]

得到的模型并不是一个工作流网，因为变迁b与模型的其他部分并不相连。这一模型允许b的执行发生在a之前或者c之后，与事件日志不一致。通过论述了这一问题，使 用α算法的改进版，可以得到图5.11所示的工作流网。

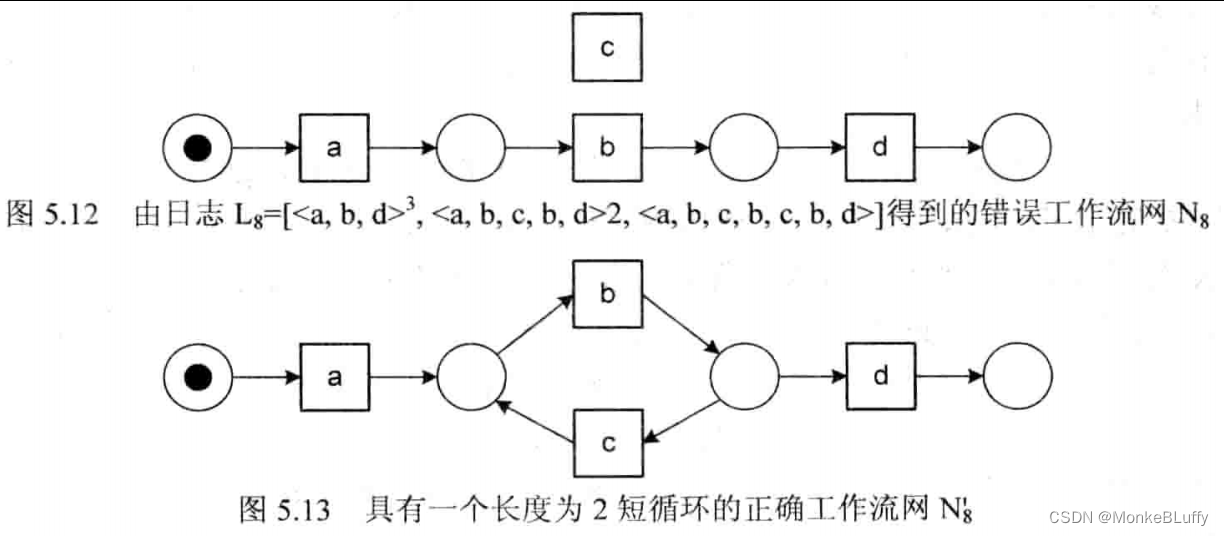
长度为2的循环问题可以通过图5.12中的Petri 网 N₈来解释，它是将基本的α算法应用到日志L₈上得到的结果。

L₈=[<a,b,d>³,<a,b,c,b,d>2,<a,b,c,b,c,b,d>]

从这个事件日志中可以得到如下基于日志的顺序关系：a→_L8b,b→_L8d 并且bll_L8c，因此基本的α算法错误地认为b 和 c 是并行的，因为它们互相跟随对方。图5.12不是一个工作流网，因为 c 并不在从源库所到汇结库所的路径上。

基本的α算法可以很好地挖掘长度为3或者更长的循环。对于包含至少3个活动 (a,b,c) 的循环，可以通过关系>L来区分并行和循环。如果是一个循环，我们只会发现 a>_Lb，b>_Lc 和 c>_La；而如果是并行，那我们会发现a>_Lb，a>_Lc，b>_La，b>_Lc，c>_La 和 c>_Lb，因此可以很容易地看出它们的不同。注意如果循环长度为2，那么情况就不同了。对于一个只含有活动 a 和 b 的循环，我们会发现 a>_Lb 和 b>_La，当活动 a 和 b 并行时，我们会发现一样的关系，此时循环和并行结构都会导致事件日志中产生相同的足迹。

一个更加困难的问题是发现非局部依赖(non-local dependencies)，它是由非自由选择过程结构产生的。图5.14给出了一个例子，观察下面的事件日志，图中的网可以很好地与它对应：

L₉={<a,c,b>⁴⁵,<b,c,e>⁴²}

可是，运用α算法得到的工作流网中不含有图中标示的库所 p₁ 和 p₂，因此，正如图5.6所示，α(L₉)=N₄，尽管轨迹<a,c,e>和<b,c,d>并没有出现在L₉中。通过使用改进版α算法可以(部分)解决这一问题。
α算法的另一个不足之处在于没有考虑次数，因此这一算法对于噪声和不完全性非常敏感。
α算法能够发现一大类模型，当遇到特殊的过程模式（如短循环和非局部依赖）时基本的八步算法有一些不足，某些不足可以通过改进算法来解决。已知模型可以使用工作流网描述并且不包含重复活动(两个变迁的活动标签相同)、无声变迁(没有被记录在事件日志中的活动)以及图5.15所示的两种结构时，α算法能够保证得到一个正确的过程模型。
即使模型使用了图5.15所示的结构，α算法仍有可能得到一个可用的过程模型。举例而言，α算法无法发现图5.14中高亮的库所 p₁和 p₂，但仍然得到了一个能够重演日志的合理的过程模型。

6.4 考虑事务生命周期

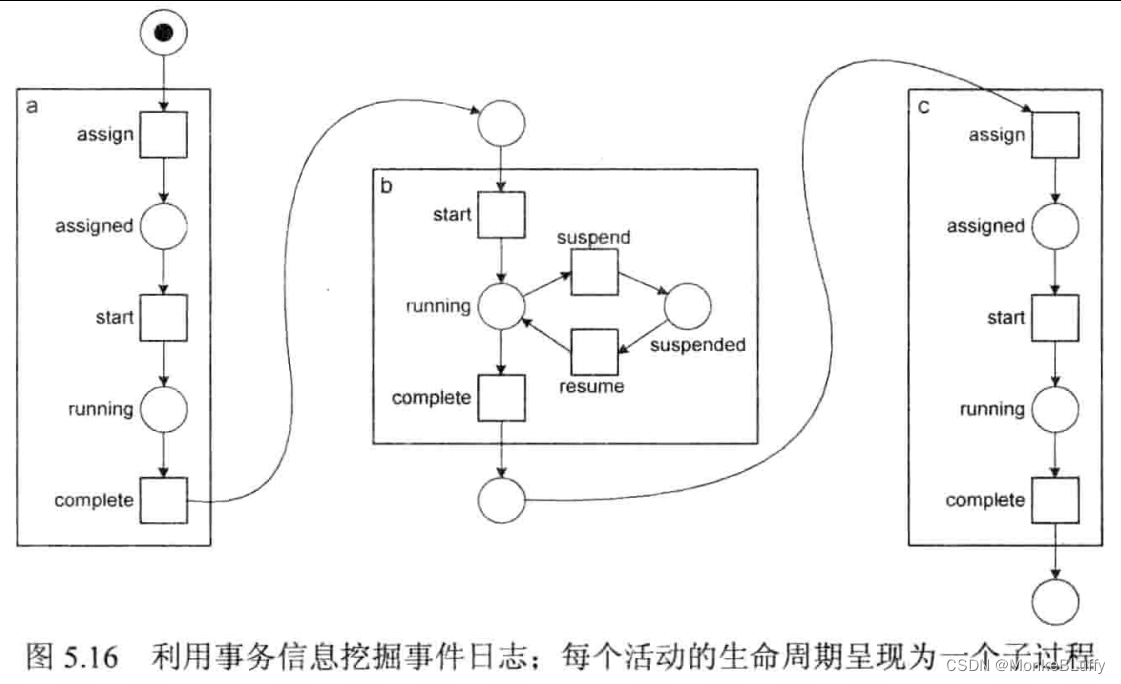
第4讲描述事件日志中的典型信息时，我们讨论了一个活动实例的事务生命周期模型。 图 4.3 展示了事务类型的例子，如计划、开始、完成和暂停。事件通常具有一个事务类型属性，例如#_trans(e)=complete，XES的标准生命周期扩展也提供了这样一个属性。可以很容易地改写α算法，使它考虑这一属性。首先，日志可以被投影为一些更小的事件日志，其中每一个日志包含与一个特定活动相关的所有事件。其次，当挖掘总过程时，可以利用整体事务生命周期信息(如图4.3所示)或者关于特定活动的事务生命周期信息，图5.16展示了利用后者的情况。与一个活动相关的所有事件被映射为变迁并嵌入到一个子过程中。可以独立地发现或者使用领域知识建模每个子过程的变迁之间的关系。图5.16展示了一个包含3个活动的串行序列。活动 a 和 c 拥有共同的事务生命周期，这一周期包含 assign、start 和 complete 3个事件类型。活动 b 的事务生命周期包含 start、suspend、resume 和 complete 4个事件类型。