一、LeetCode198.打家劫舍(线性)
题目链接/代码讲解/视频讲解:https://programmercarl.com/0198.%E6%89%93%E5%AE%B6%E5%8A%AB%E8%88%8D.html
状态:已解决
1.思路
这个题的关键就在于想清楚如何抉择某个房间偷不偷的问题。根据题目,我们知道不能连续进入两间屋子偷窃。也就是说,当前屋子偷不偷取决于前一个房屋与前两个房屋是否被偷(其明面上只与前一个有关,但如果前一个屋子没有偷过,那当前屋子就可以再偷,因此需要对比截止到前两个屋子的偷窃最高金额数+当前屋子的金额 与 偷上一个屋子累积的偷窃最高金额)。
(1)确定dp数组以及下标含义:
dp[i]:考虑下标 i (包括i)以内的房屋,最多可以盗窃的金额为i。
(2)确定递推公式:
dp[i]只有两种来源:
① 偷i,则说明 i-1 没被偷,不考虑后面的屋子时,当然是偷了这个屋子的钱总金额最大,故此时dp[i] = dp[i-2]+nums[i];
② 不偷i,则说明 i-1 可能偷了也可能没偷,但由于 dp[i-1]代表的是i-1这个屋子所有情况中盗取金额的最大值,故不管i-1偷没偷,我们只需要这个最大值就行,那么此时dp[i]继承dp[i-1],即dp[i] = dp[i-1]。
取两者中的最大值,即:dp[i] = max(dp[i-2] + nums[i],dp[i-1]);
(3)dp数组初始化:
由于要看前两个屋子的状态,故需要初始化dp[0]和dp[1],从dp[i]的定义上来讲,dp[0] 一定是 nums[0],dp[1](前两个屋子能够盗窃的最大金额)就是nums[0]和nums[1]的最大值即:dp[1] = max(nums[0], nums[1]);
其余下标的值为0,防止值被覆盖。
(4)确定遍历顺序:
dp[i]是根据前面dp[i-1]和dp[i-2]推出来的,因此一定是从前往后去推。
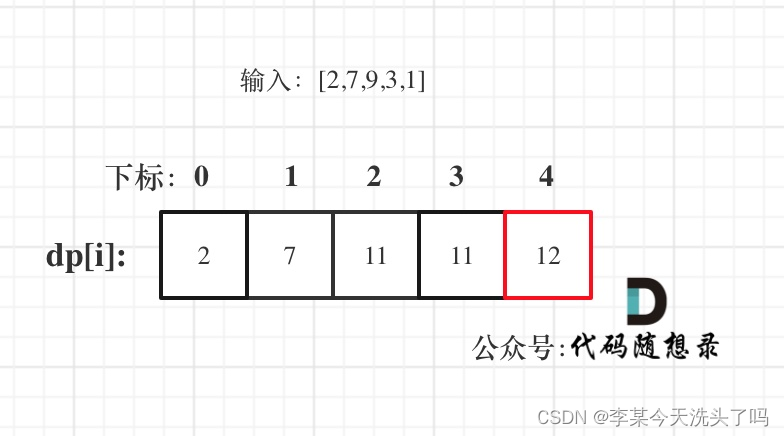
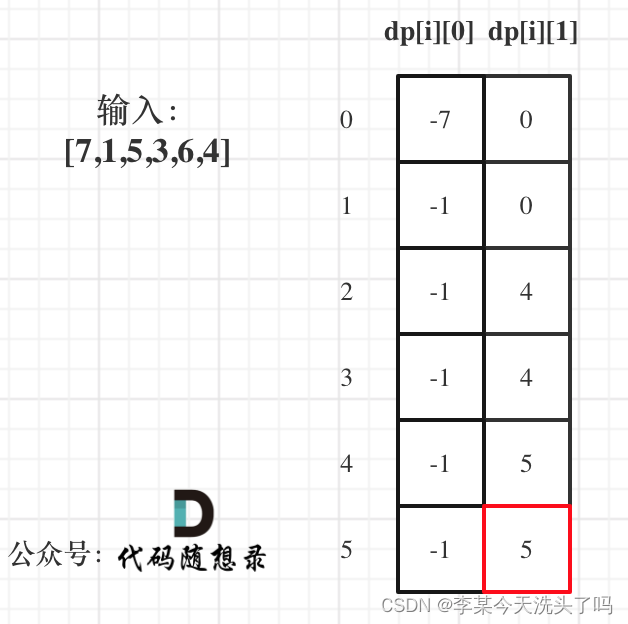
(5)举例推导dp数组:
以示例二为例:
dp[nums.size()-1]为结果。
2.代码实现
class Solution {
public:
int rob(vector<int>& nums) {
vector<int> dp(nums.size(),0);
if(nums.size()==1) return nums[0];//注意这种特殊情况
dp[0] = nums[0];
dp[1] = max(nums[0],nums[1]);
for(int i=2;i<nums.size();i++){
dp[i] = max(dp[i-2]+nums[i],dp[i-1]);
}
return dp[nums.size()-1];
}
};时间复杂度: O(n)
空间复杂度: O(n)
二、213.打家劫舍II(环形)
题目链接/代码讲解/视频讲解:https://programmercarl.com/0198.%E6%89%93%E5%AE%B6%E5%8A%AB%E8%88%8D.html
状态:已解决
1.思路
这道题跟上面的区别是上面的房间呈直线排列,而这道题的房间是环形排列的。环形意味着首尾相连,因此,我们比线性排列的房间多个限制条件:首尾的房间不能同时盗窃。这个很好实现,我们先去掉尾部的房间按线性房间的方法求一个最大金额,再去掉首部的房间按线性房间的方法求一个最大金额,然后取二者最大值。
有的同学可能会想,要是最大情况是首尾房间都不偷的话,那我们是不是漏情况了?并没有!我们在求线性房间的最大金额时说了,dp[i]是考虑范围0~i,不代表第i个房间就被偷了,dp[i]包含了第i个房间的所有可能情况。
这么分析后,基本上跟上道题就大差不差了。
2.代码实现
class Solution {
public:
int rob(vector<int>& nums) {
if(nums.size() == 1) return nums[0];
if(nums.size() == 2) return max(nums[0],nums[1]);
int result1 = linarRob(nums,0,nums.size()-1);
int result2 = linarRob(nums,1,nums.size());
return max(result1,result2);
}
int linarRob(vector<int>& nums,int start,int end) {
vector<int> dp(end-start+1,0);
if(nums.size()==1) return nums[0];//注意这种特殊情况
dp[start] = nums[start];
dp[start+1] = max(nums[start],nums[start+1]);
for(int i=start+2;i<end;i++){
dp[i] = max(dp[i-2]+nums[i],dp[i-1]);
}
return dp[end-1];
}
};时间复杂度: O(n)
空间复杂度: O(n)
三、337.打家劫舍III (树形)
题目链接/代码讲解/视频讲解:https://programmercarl.com/0337.%E6%89%93%E5%AE%B6%E5%8A%AB%E8%88%8DIII.html
状态:已解决
1.思路
此题也是一个典型的打家劫舍问题,只是对比上两道题又进行了一个升级,变成了树形房间。树形结构中,父节点与左右子节点的偷窃状态有以下几种状态:
(1)偷父节点,那么左右节点一定都不偷,那么父节点的最大金额就是自身金额+左右节点不偷的最大金额的和。
(2)不偷父节点,那么左右节点可偷可不偷,那么父节点的最大金额就是左右节点偷或者不偷的最大金额的和。
很明显一个节点的最大金额要根据子节点的最大金额决定,因此这题要递归,且是后序遍历的顺序(左右中)。同时,如何取子节点的最大金额也要依赖父节点的偷窃状态,因此需要动规。
故此题就是一个二叉树和动态规划结合的题,需要在树上进行状态转移,也就是俗称的树形dp。
以递归三部曲为框架,其中融合动规五部曲的内容来进行讲解。
(1)确定递归函数的参数以及返回值(dp数组以及下标含义):
我们知道需要子节点偷和不偷两种情况的最大金额,因此每层都需要两个容器来保存这两种情况,那我们需要定义2*n大小的数组吗?并不需要!由于递归的特性,我们只需要每层都有一个两个元素的数组即可:即dp[0]代表该节点不偷时的最大金额,dp[1]代表该节点偷时的最大金额。
知道了dp数组的构造,我们就能更进一步地得出递归函数的参数和返回值了。根据我们刚刚的分析,是需要子节点两个状态的最大金额数的,因此子节点要返回给我们它的两个状态的值,故返回值就是dp数组,也就是说返回值类型是vector<int>。参数就是当前需要计算的节点的指针。
(2)确定终止条件(dp数组初始化):
在遍历的过程中,如果遇到空节点的话,很明显,无论偷还是不偷都是0,所以就返回。
(3)确定单层递归的遍历逻辑(递推公式、遍历顺序):
就是刚刚分析的两种情况:
① 偷父节点,那么左右节点一定都不偷,那么父节点的最大金额就是自身金额+左右节点不偷的最大金额的和。
② 不偷父节点,那么左右节点可偷可不偷,那么父节点的最大金额就是左右节点偷或者不偷的最大金额的和。
根据这两种情况的分析,遍历顺序就可以很容易地确定为后序遍历的顺序(需要先知道左右节点的值才能计算出父节点的值,故左右中)。
同时根据这两种情况的分析,可以得到递推公式:(now) dp[1] = (left) dp[0] + (right) dp[0] + cur->val,(now)dp[0] = max((left) dp[0] ,(left) dp[1]) + max((right) dp[0] ,(right) dp[1])。
(4)确定单层递归逻辑:
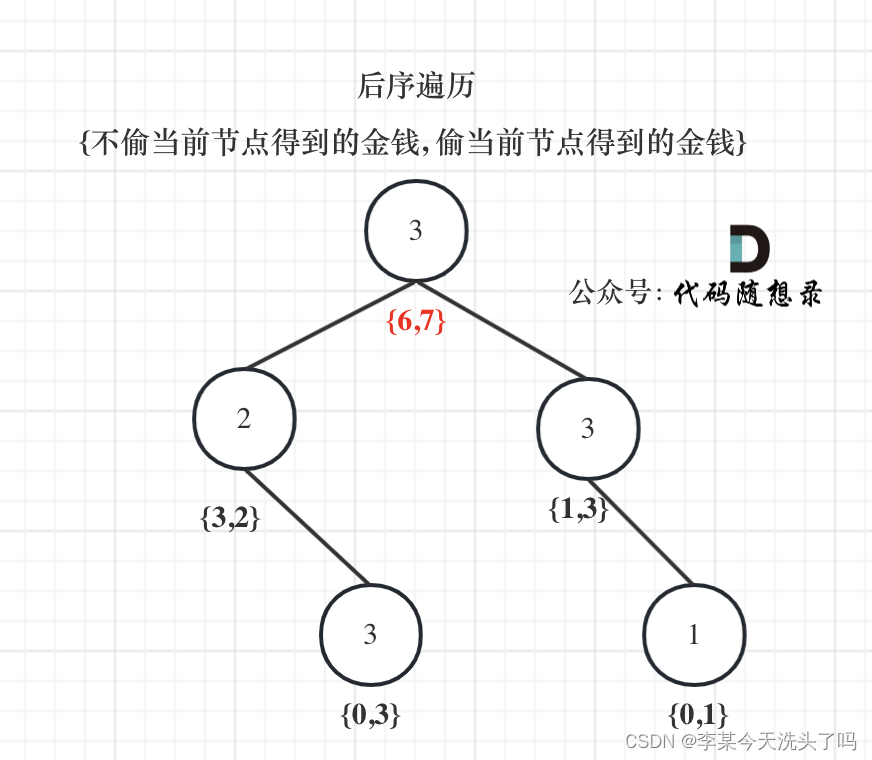
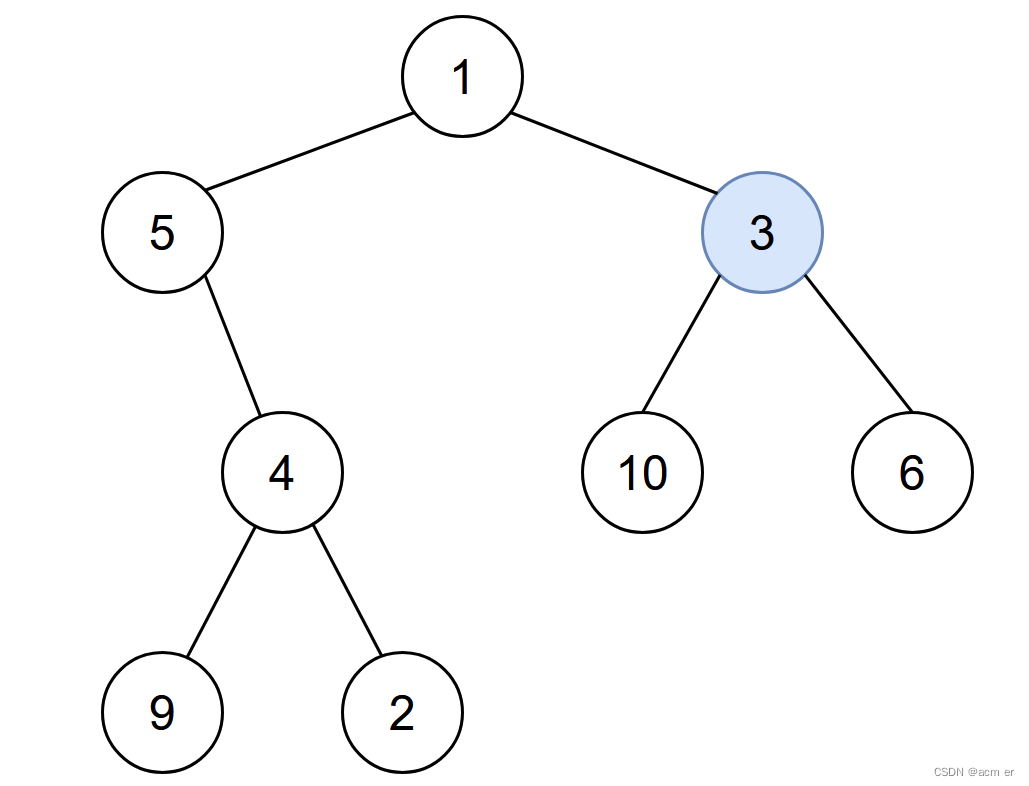
以示例1为例,dp数组状态如下:(注意用后序遍历的方式推导)
最后头结点就是取dp[0]和dp[1]的最大值。
2.代码实现
class Solution {
public:
vector<int> treeRob(TreeNode * node){
vector<int> dp(2,0);
if(node == NULL) return {0,0};
vector<int> left = treeRob(node->left);
vector<int> right = treeRob(node->right);
dp[1] = node->val + left[0] + right[0];
dp[0] = max(left[0],left[1]) + max(right[0],right[1]);
return dp;
}
int rob(TreeNode* root) {
vector<int> dp = treeRob(root);
return max(dp[0],dp[1]);
}
};时间复杂度:O(n),n为节点个数,每个节点只遍历了一次
空间复杂度:O(logn)