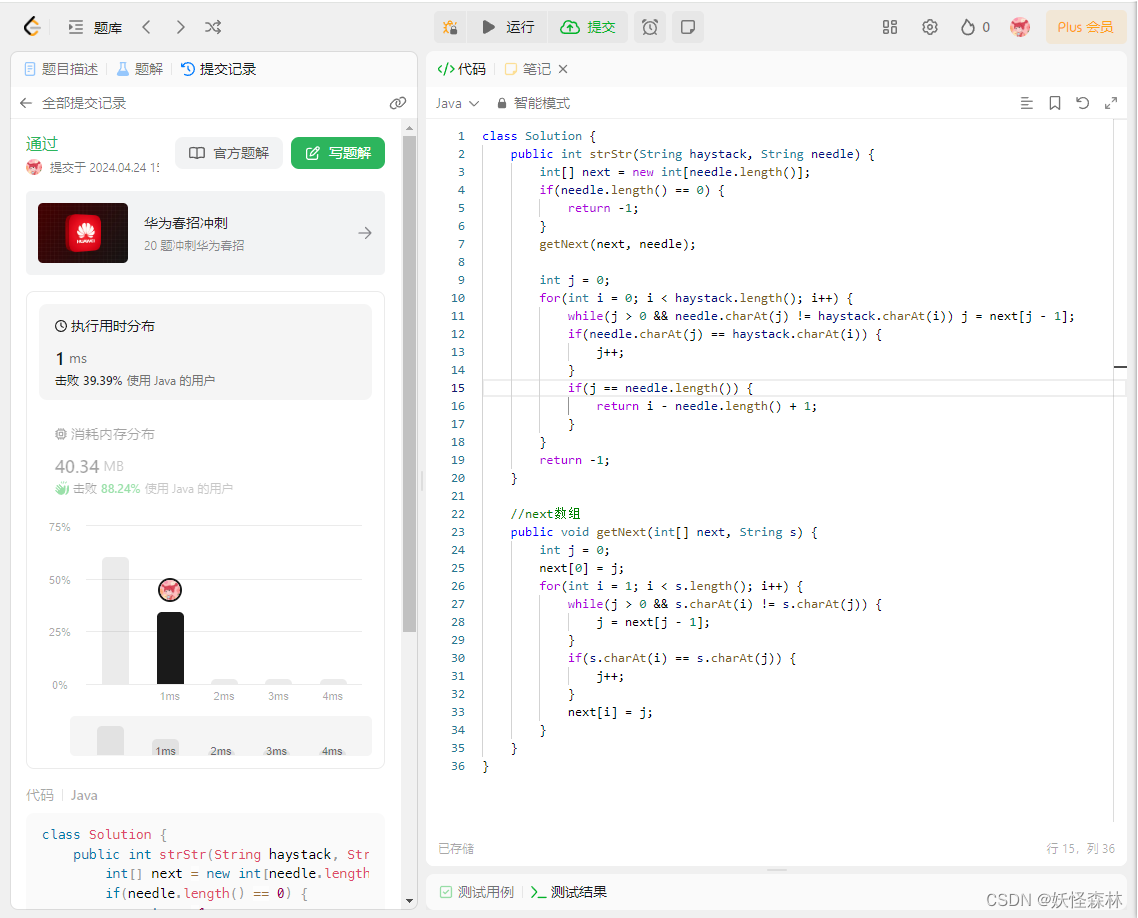
六、实现strStr()
题目:
力扣28:找出字符串中第一个匹配的下标
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
示例1:
输入:haystack = “sadbutsad”, needle = “sad”
输出:0
解释:“sad” 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ,所以返回 0 。
示例2:
输入:haystack = “leetcode”, needle = “leeto”
输出:-1
解释:“leeto” 没有在 “leetcode” 中出现,所以返回 -1 。
提示:
- 1 <= haystack.length, needle.length <= 104
- haystack 和 needle 仅由小写英文字符组成
解题思路分析:
本题是KMP 经典题目。
KMP算法理论基础:
KMP算法的名字由来:
因为是由这三位学者发明的:Knuth,Morris和Pratt,所以取了三位学者名字的首字母。所以叫做KMP。
KMP算法解决的问题:
解决字符串匹配的问题;在文本串种查找是否出现过模式串。
例如:
- 文本串:aabaabaafa
- 模式串:aabaaf
暴力匹配: 从下标0处开始,匹配失败后回到下标1处开始重新匹配;时间复杂度为O(m+n)
KMP: 出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配了。

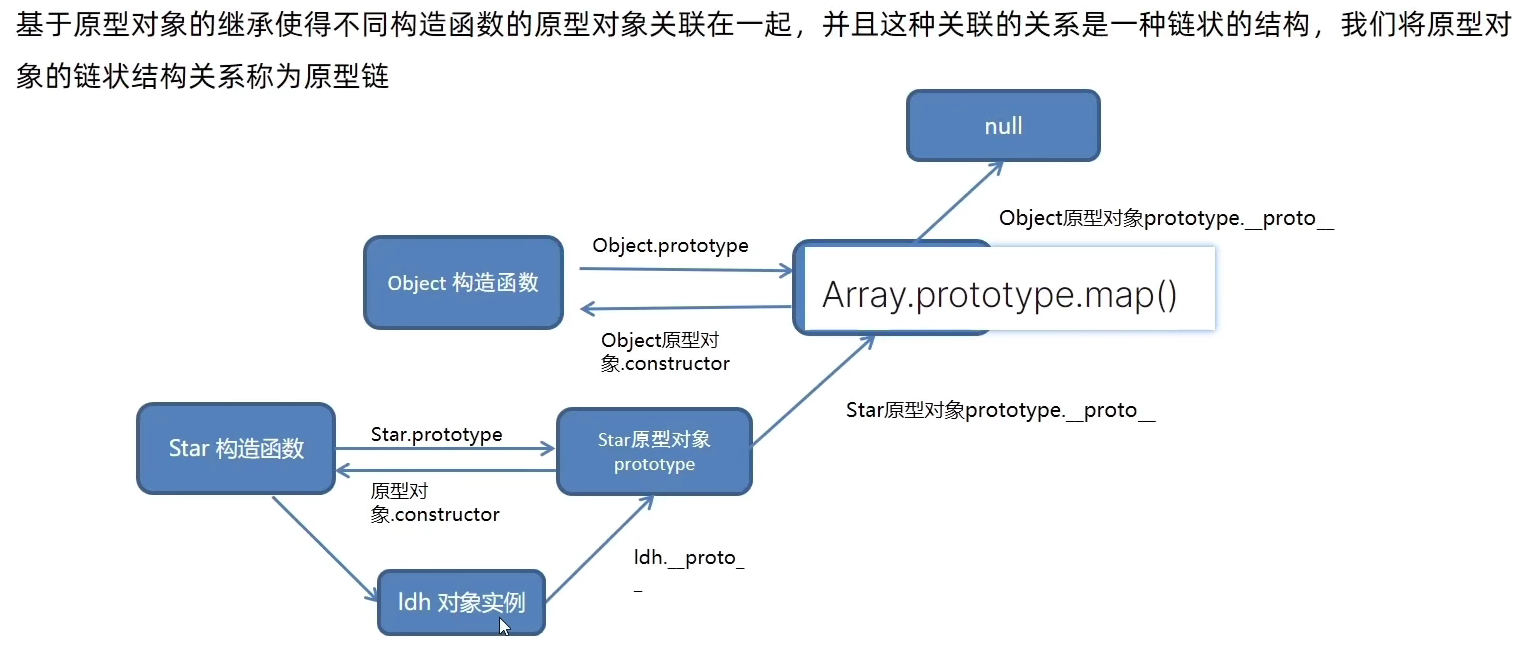
前缀表:
KMP可以通过前缀表来做到跳到b直接去继续匹配;
前缀表是用来回退的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。
前缀:不包含尾字母的所有子串;
- a;aa;aab;aaba;aabaa
后缀:不包含首字母的所有子串;
- f;af;aaf;baaf;abaaf
最长相等前后缀:
- a 最长相等前后缀为0;
- aa 最长相等前后缀为1;
- aab 最长相等前后缀为0;
- aaba 最长相等前后缀为1;
- aabaa 最长相等前后缀为2;
- aabaaf 最长相等前后缀为0;
前缀表如下图所示:
使用前缀表的匹配过程:
当指针移动到f时,发现字符串不匹配,那么就跳到最长相等前缀的后面,也就是跳到最后一个a对应的前缀表数字的位置,即跳到下标为2的位置继续匹配;也就是从b继续匹配。
因为前缀表中的2表示的就是相等前后缀的长度,要跳到前缀的后面,前缀的后面的下标正好就是前缀的长度2。
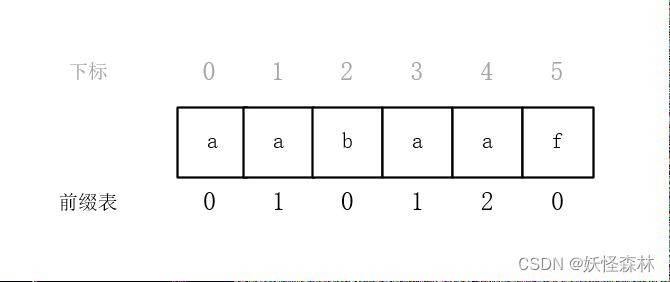
next数组:
next数组放的也是前缀表,但是可能会有一些调整;
next数组就是遇见冲突以后告诉我们要回退到哪个位置,所以称为next数组。
很多KMP算法具体实现过程中,next数组会把前缀表做一个整体-1的操作;前缀表就变成-1,0,-1,0,1,-1了;但是具体匹配过程中还会做+1操作,原理都是一样的;直接将前缀表原封不动的放入next数组中也能完成匹配。
代码实现:
有的实现是把前缀表整体右移一个位置,第一个位置变成-1;
有的实现是把前缀表整体-1;
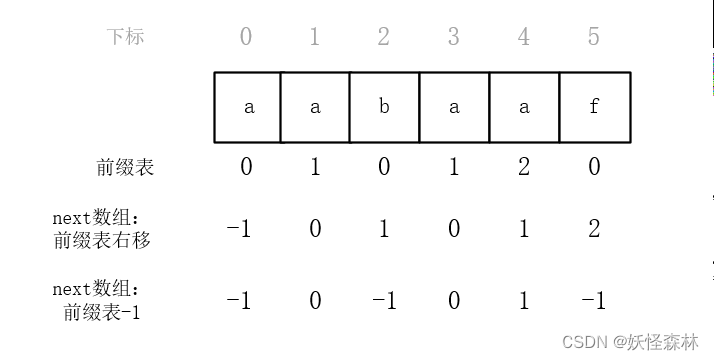
文本串:aabaabaaf
模式串:aabaaf
把前缀表整体右移作为next数组:这种实现方式是直接在遇到冲突的位置也就是f所在位置进行跳转,跳转到b;
也就是在遇见冲突的时候,寻找位置的方式不一样;要么是找冲突位置的前一个位置对应的next数组值;要么就是直接找冲突位置对应的next数组值;原理都是一样的。
获得next数组分为以下几步:
- 初始化
- 前后缀不相同
- 前后缀相同
- 更新next数组
//初始化
//指针i和指针j;j是指向前缀末尾位置(最长相等前后缀的长度);i是指向后缀末尾位置
int[] next = new int[needle.length()];
int j = 0; //前缀从0开始
next[0] = j;
//求next数组:比较前缀和后缀所对应的字符是否相等,i从1开始才能和j进行比较,所以i初始化为1
for(int i = 1; i < needle.length(); i++) {
//处理前后缀不相同的情况
//当needle[i]不等于needle[j]的时候,就相当于在i这个位置发生了冲突,那么j就需要回退到j的前一位对应的next数组的位置;相当于在i这里发生冲突的时候,j回退到j-1对应的next[j-1]的位置,继续重新匹配前后缀
while(s[i] != s[j]) j = next[j-1];
//处理前后缀相同的情况
if(s[i] == s[j]) j++;
//更新next数组
next[i] = j;
}
题解: