关注我,持续分享逻辑思维&管理思维; 可提供大厂面试辅导、及定制化求职/在职/管理/架构辅导;
有意找工作的同学,请参考博主的原创:《面试官心得--面试前应该如何准备》,《面试官心得--面试时如何进行自我介绍》, 《做好面试准备,迎接2024金三银四》。
推荐热榜内容:《C#实例:SQL如何添加数据》
-------------------------------------正文----------------------------------------
深度搜索和广度搜索算法
又称DFS和BFS。深度优先搜索的原理是:首先选择一个顶点作为起始点,接着从他各个相邻点出发进行依次访问,直到所有与起始点有路径相通的顶点都被访问到。若此时有没被访问到的节点,则选择一个其他顶点进行再次访问。
广度优先搜索的原理是:选择一个顶点作为起始点,依次访问该起始点的所有邻接点,再根据邻接点访问他们各自的邻接点,并保证先访问节点的邻接点先与后访问节点的邻接点被访问。

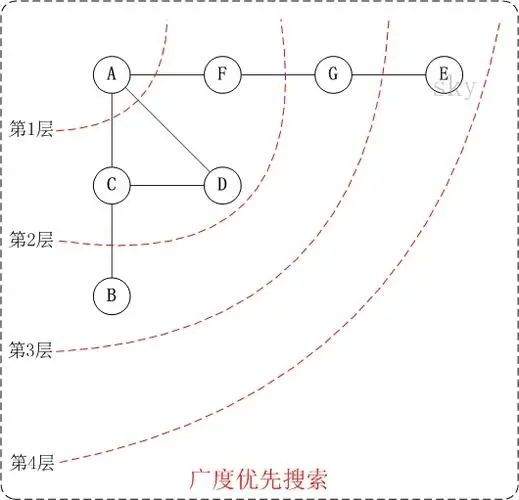
假设我们有一个无向图,用邻接矩阵表示,我们需要实现DFS来遍历所有的顶点。
#include <iostream>
#include <vector>
using namespace std;
void dfs(vector<vector<int>>& graph, vector<bool>& visited, int start) {
visited[start] = true;
cout << start << " ";
for (int i = 0; i < graph[start].size(); ++i) {
if (!visited[graph[start][i]]) {
dfs(graph, visited, graph[start][i]);
}
}
}
int main() {
int n = 4; // 假设图有4个顶点
vector<vector<int>> graph = {{1, 2}, {0, 2}, {0, 3}, {1, 3}}; // 邻接矩阵
vector<bool> visited(n, false); // 访问标记数组
// 从顶点0开始深度优先搜索
dfs(graph, visited, 0);
return 0;
}在这个例子中,dfs函数是深度优先搜索的核心,它使用一个递归函数来访问还未访问的每个顶点,并且用cout语句输出当前访问的顶点编号。visited数组用于记录每个顶点是否已经被访问过。
这个例子假设图是用邻接矩阵表示的,并且没有负权边或自环。如果需要处理带权图或者不规则图结构,你可能需要修改代码以适应相应的数据结构和算法细节。
广度搜索算法通常用于遍历或搜索图、树等结构的节点,以便找到从起始节点到目标节点的最短路径或执行其他任务。下面是一个简单的C++实现示例,使用队列来实现广度搜索算法。
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
// 广度优先搜索算法
void bfs(vector<vector<int>>& graph, int start, int target) {
queue<int> q;
vector<int> visited(graph.size(), 0);
q.push(start);
visited[start] = 1;
while (!q.empty()) {
int node = q.front();
q.pop();
if (node == target) {
cout << "找到了目标节点!" << endl;
return;
}
for (int neighbor : graph[node]) {
if (!visited[neighbor]) {
q.push(neighbor);
visited[neighbor] = 1;
}
}
}
cout << "未找到目标节点。" << endl;
}
int main() {
// 图的表示
vector<vector<int>> graph = {
{1, 2},
{0, 3},
{0, 4},
{3, 4}
};
// 广度优先搜索的起点和目标节点
int start = 0;
int target = 4;
bfs(graph, start, target);
return 0;
}这段代码定义了一个bfs函数,它接受一个图(用邻接列表表示的邻接矩阵)、一个起始节点和一个目标节点作为参数。使用一个队列来保存待访问的节点,并且使用一个标志数组visited来记录哪些节点已经被访问过。如果找到了目标节点,算法将停止,否则输出未找到目标节点。