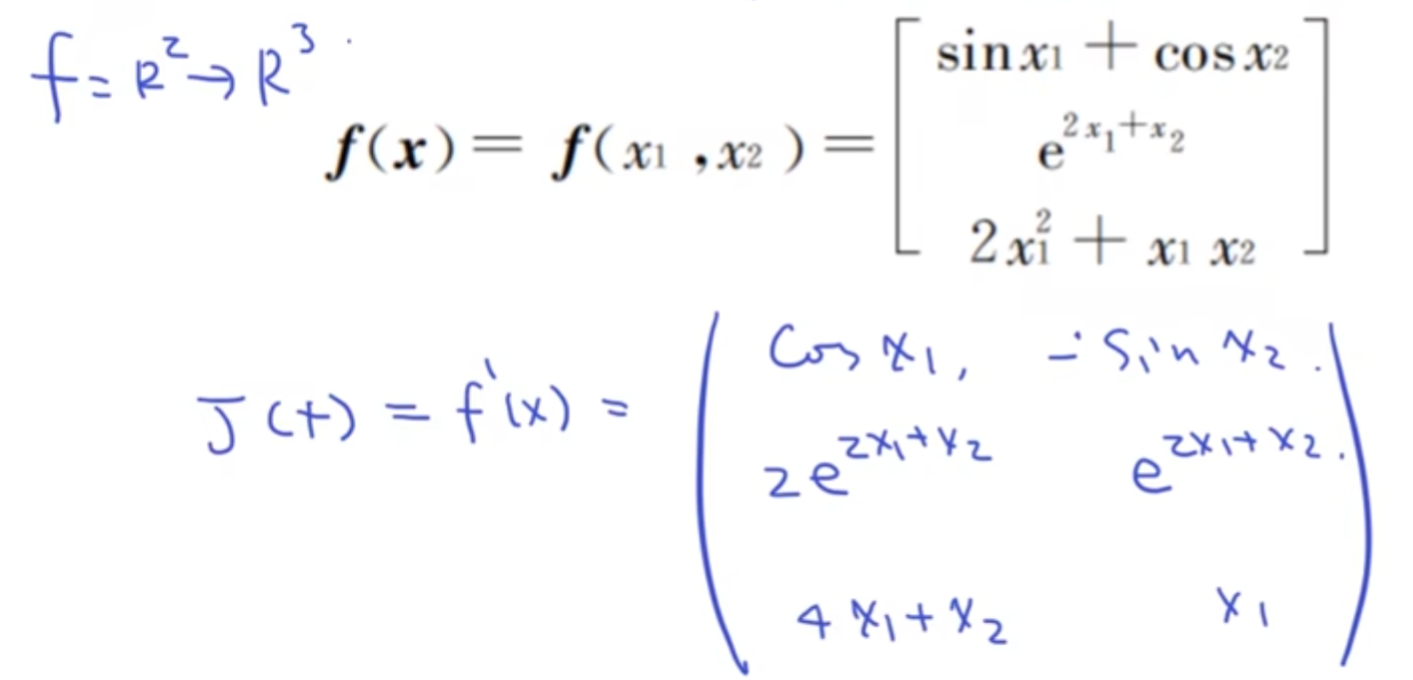一、题目解析:

二、知识回顾:
1.二维数组:
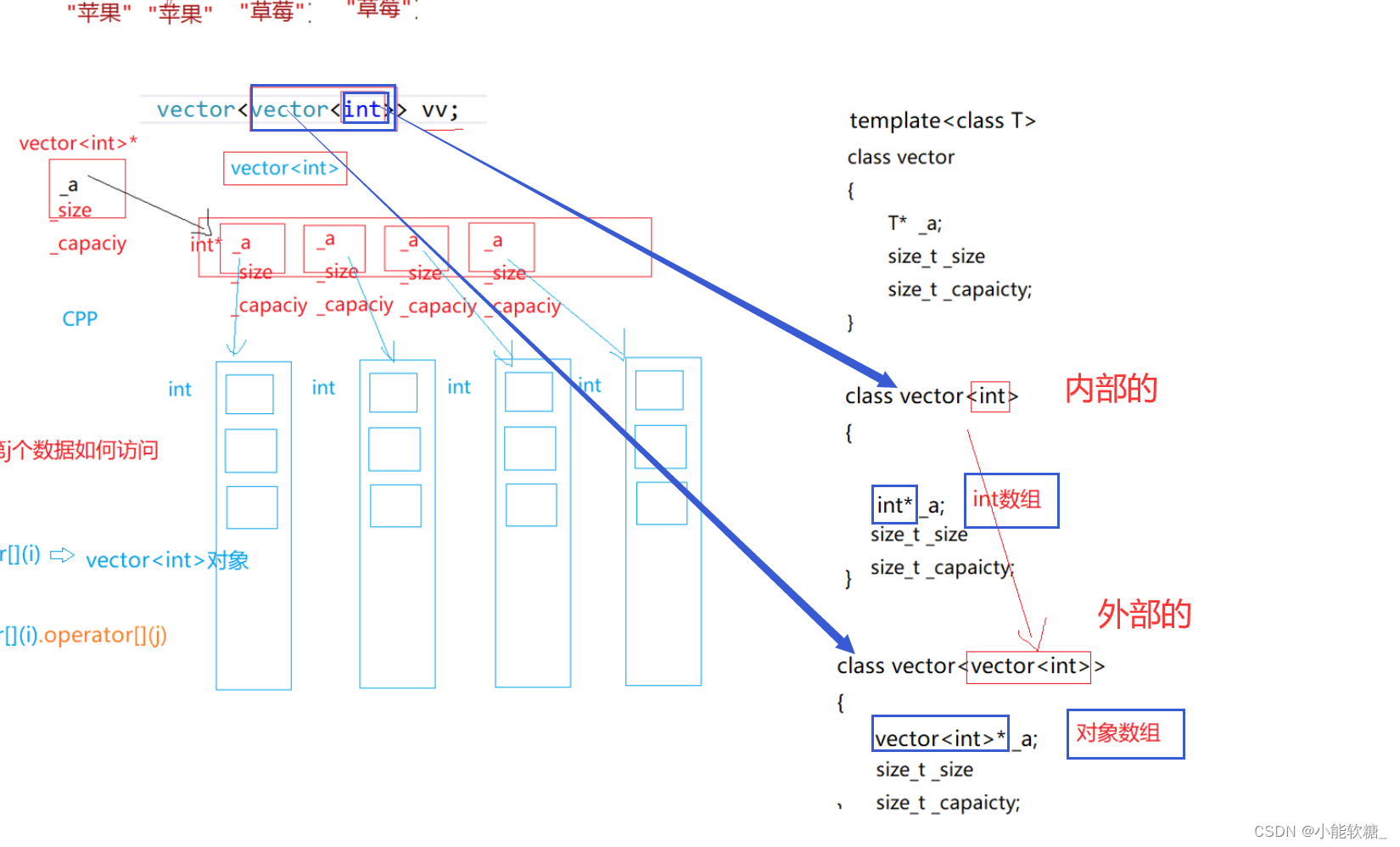
2. C语言中的二维数组访问方式和vector二维数组的访问,
不同区别:
(1)表面是一样的,但底层不同!
(2)静态二维数组在底层本质上也是一维数组的连续!(二维数组的数组名是:第1行数组的地址)
(3)C语言中的二维数组本质上是指针解引用!

(4)vector<vector>访问数据本质上是:operator[ ]函数的调用!
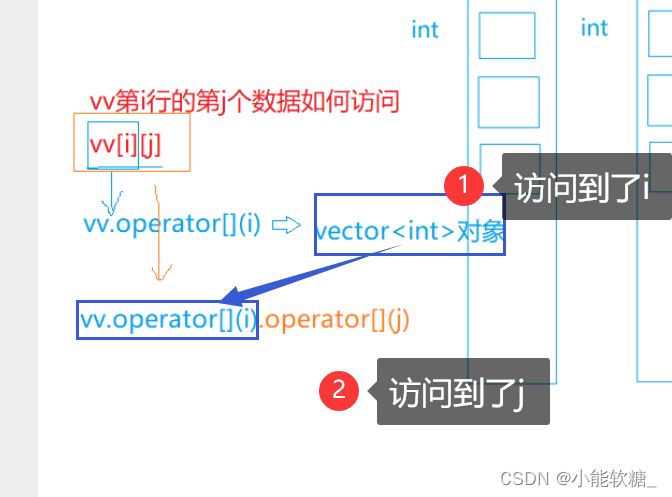
三、解题思路:
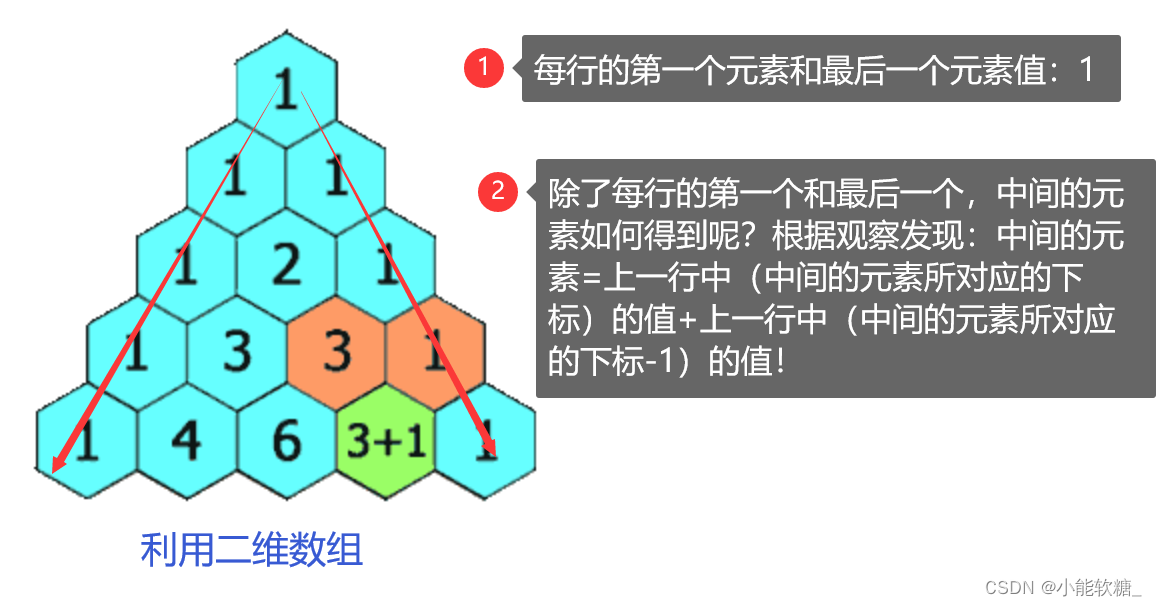
四、代码实现:
class Solution
{
public:
vector<vector<int>> generate(int numRows)
{
// 1.创建二维数组
vector<vector<int>> vv;
// 2.开辟 行
vv.resize(numRows);
for(size_t i=0;i<numRows;i++)
{
// 3.开辟:每一行有多少列,并把所有元素都初始化为0(第0行,有1列;第1行,有2列)
vv[i].resize(i+1,0);
// 有规律得:每1行的第1个元素和最后1个元素都为:1
vv[i][0]=vv[i][vv[i].size()-1]=1;
}
// 4.接下来就处理夹在中间的元素的规律=上一行两个元素相加之和
for(size_t i=0;i<numRows;i++)
{
for(size_t j=0;j<i+1;j++)
{
if(vv[i][j]==0)//这里我之前初始化为0,就很巧妙的判断出哪些是中间的元素。
{
vv[i][j]=vv[i-1][j-1]+vv[i-1][j];
}
}
}
return vv;
}
};