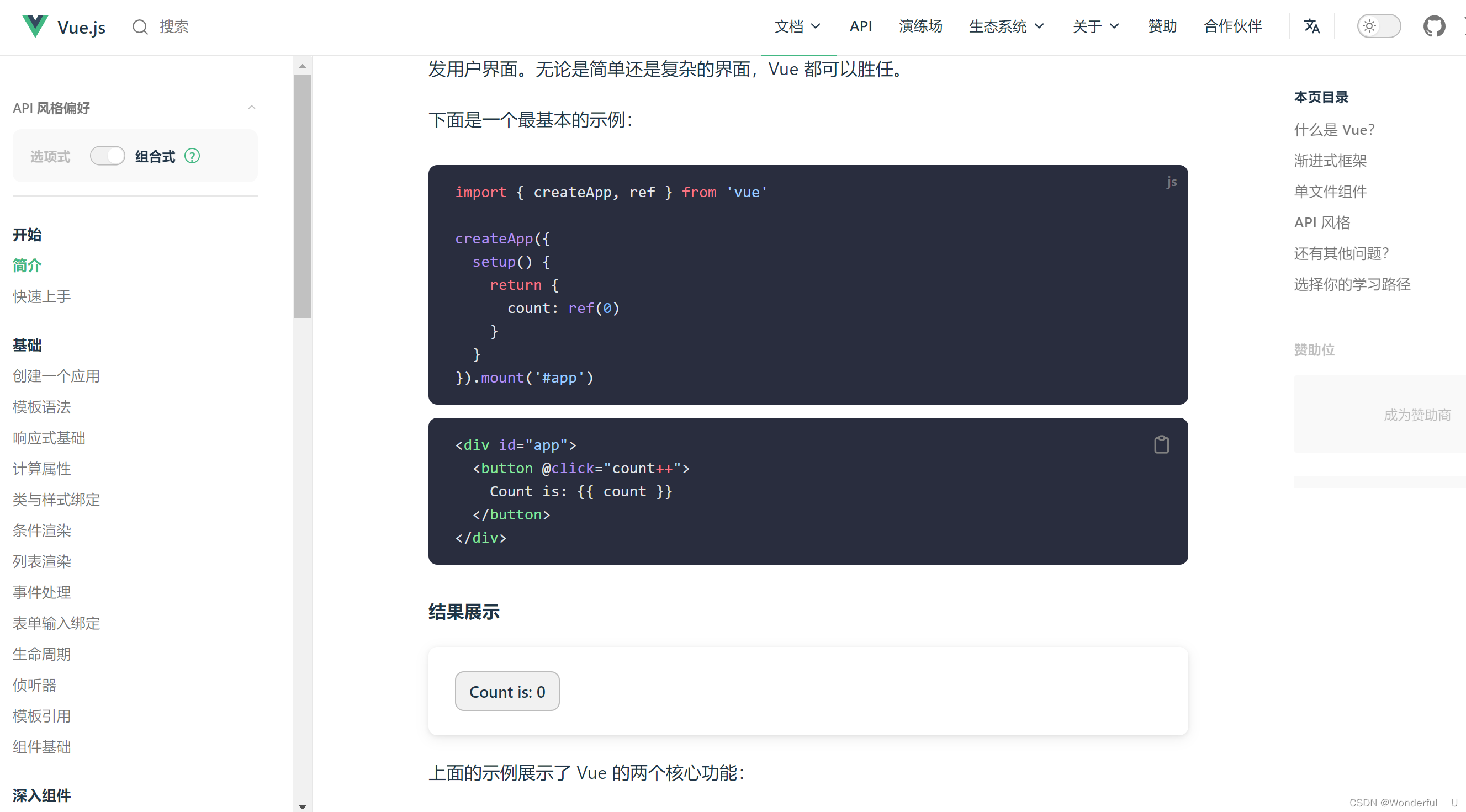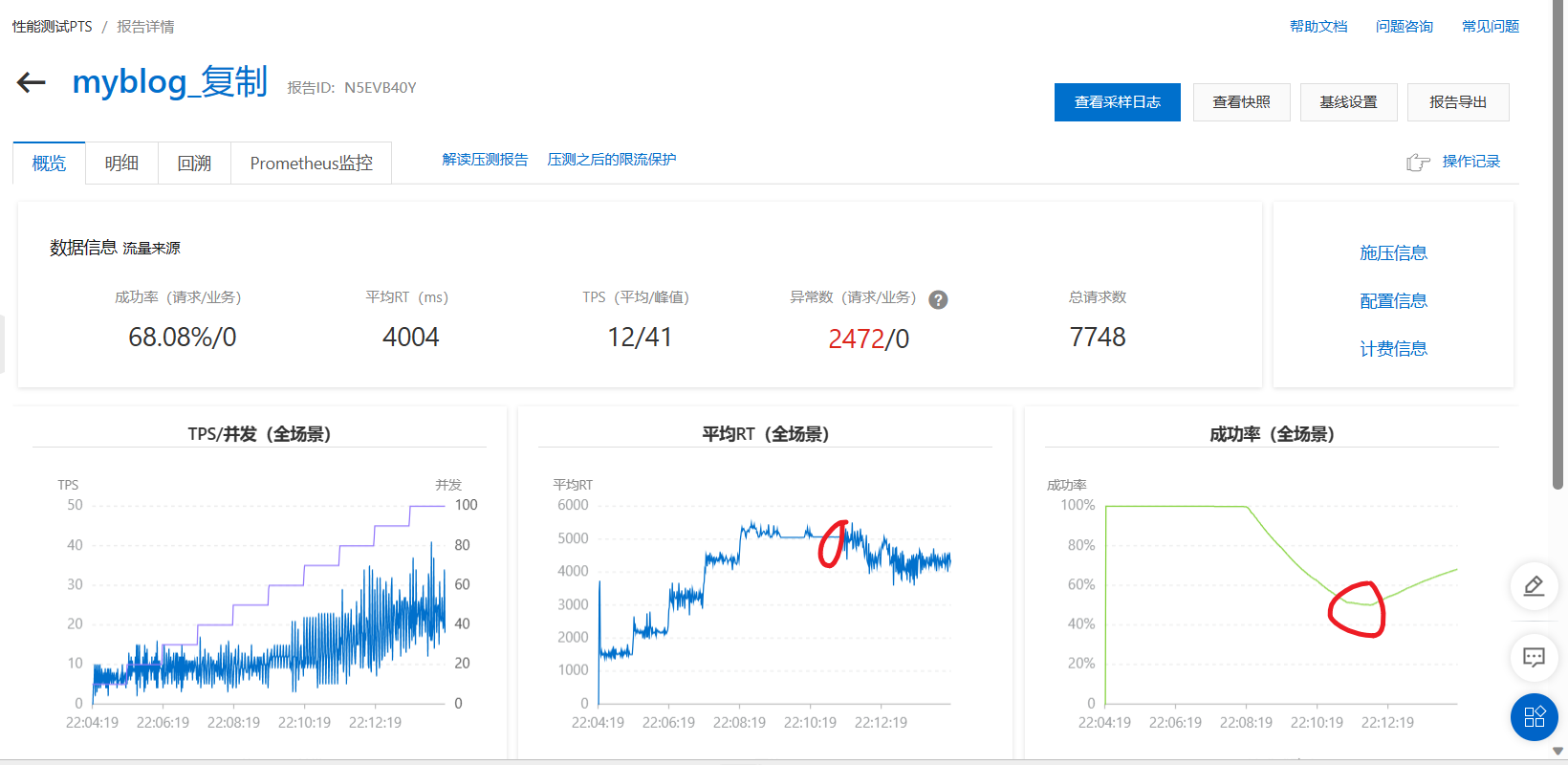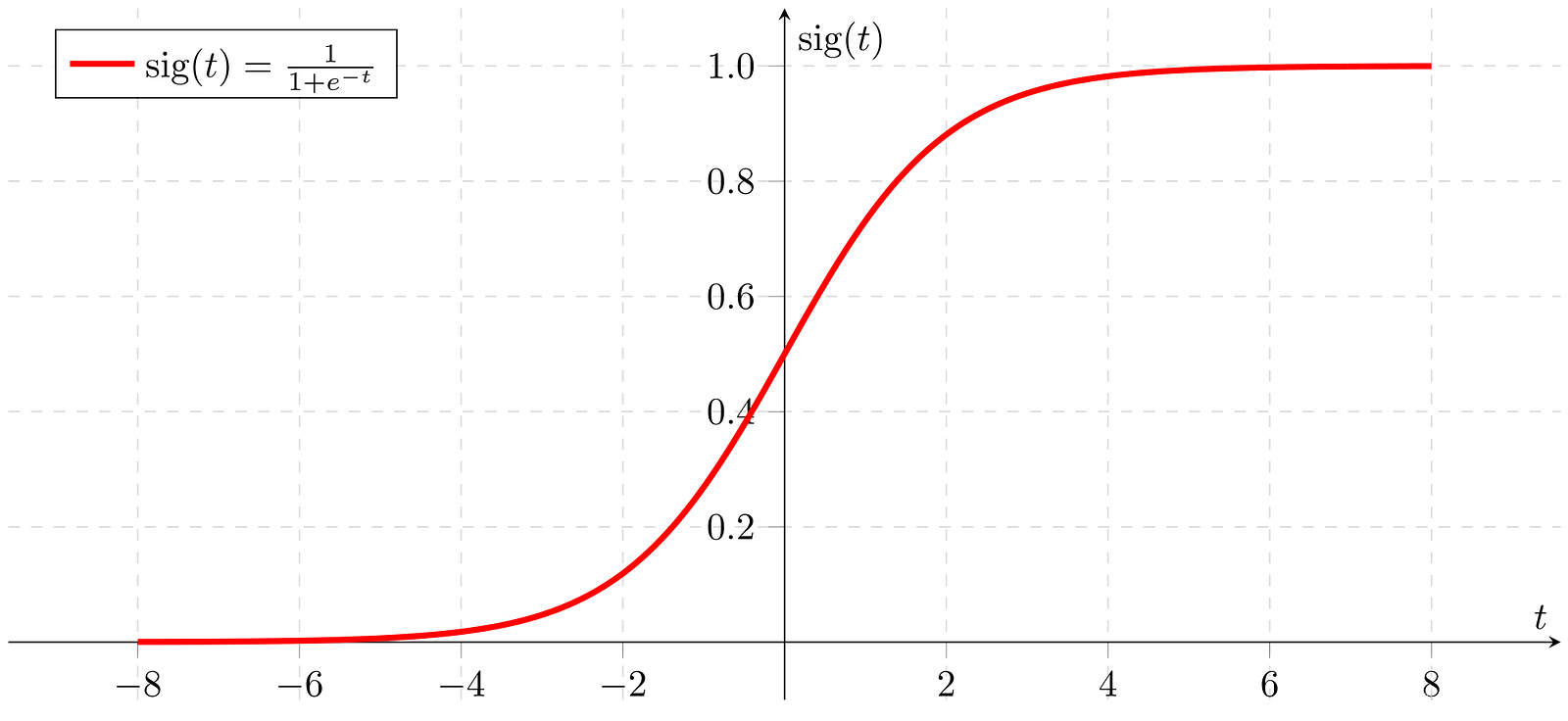
Sigmoid函数是一种常用的激活函数,其数学公式为:
σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1 + e^{-x}} σ(x)=1+e−x1
其中, x x x 是函数的输入, σ ( x ) \sigma(x) σ(x) 是函数的输出。
sigmoid函数在神经网络中常被用于二元分类任务,因为它可以将输入转换成概率值。Sigmoid函数是一个在生物学中常见的S型函数,也称为逻辑函数,它可以将一个实数映射到(0,1)的区间内。在深度学习和机器学习的上下文中,它经常被用作神经元的激活函数,因为它可以将任意输入压缩到0和1之间,从而方便地进行概率解释。
需要注意的是,当输入 x x x非常大或非常小时,Sigmoid函数的梯度会变得非常小,这可能导致在训练神经网络时出现梯度消失的问题。因此,在实际应用中,有时会选择使用其他的激活函数,如ReLU(Rectified Linear Unit)等。
通俗的举个sigmoid的例子
当用sigmoid函数进行二分类时,通常会将模型的输出解释为样本属于正类别的概率。举个例子,假设我们有一个二分类任务,要预测一封电子邮件是否为垃圾邮件。
我们的模型输出一个实数,表示该电子邮件是垃圾邮件的可能性。然后,我们将这个实数输入sigmoid函数中,得到一个在0到1之间的值,表示该邮件是垃圾邮件的概率。
例如,如果模型输出0.7,表示有70%的概率该邮件是垃圾邮件,那么将0.7作为sigmoid函数的输入,经过计算后,得到sigmoid(0.7) ≈ 0.67,即67%的概率该邮件是垃圾邮件。
类似地,如果模型输出为0.3,表示有30%的概率该邮件是垃圾邮件,那么将0.3作为sigmoid函数的输入,经过计算后,得到sigmoid(0.3) ≈ 0.57,即57%的概率该邮件是垃圾邮件。
在这个例子中,sigmoid函数将模型的输出映射到0到1之间的概率,帮助我们进行二分类预测。