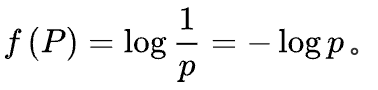RB-tree

平衡二叉搜索树
元素排列规则有利于search 和 insert

red-black tree(红黑树)是平衡二元搜索树(balanced binary tree)。其特征：排列规则有利于Search和Insert，并保持适度平衡—无任何节点过深。rb_tree提供两种插入操作:inset_unique和insert_equal。前者需要key在树是独一无二的(multimap/set不适用)，后者key可以重复存在。

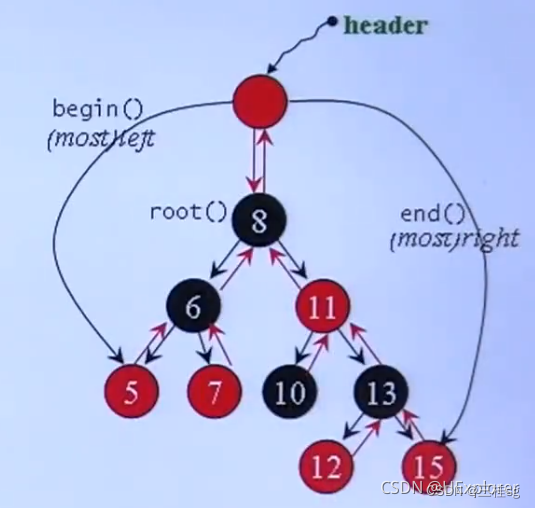
红黑树：value = key + data
class KeyOfValue: 怎么从value种取出key
Compare：Compare(比较key的大小的方法)

template<class Key,class Value,class KeyOfValue,class Compare,class Alloc=alloc>
class rb_tree
{
protected:
	typedef __rb_tree_node<Value> rb_tree_node;
public:
	typedef rb_tree_node* link_type;
protected:
	size_type node_count;	//rb_tree的节点数量
    link_type header;		//头节点
    Compare Key_compare;	//Key排序方式
};

rb_tree在使用中需要你提供4个参数：Key、Value、KeyofValue(提取Key的方法)、Compare(比较key的大小的方法)。

template <class T>
struct identity:public unary_function<T,T>{
    const T& operator()(const T& ref)const
    {
        return ref;
	}
}

template <class T>
struct less:public binary_function<T,T,bool>{
    bool operator()(const T&x,const T&y){
        return x<y;
    }
}

void RbTreeTest(){
    _Rb_tree<int,int,identity<int>,less<int>> tree;
    cout << itree.empty() << endl;  //1
	cout << itree.size() << endl;   //0

	itree._M_insert_unique(3);
	itree._M_insert_unique(8);
	itree._M_insert_unique(5);
	itree._M_insert_unique(9);
	itree._M_insert_unique(13);
	itree._M_insert_unique(5);  //no effect, since using insert_unique().
	cout << itree.empty() << endl;  //0
	cout << itree.size() << endl;   //5
	cout << itree.count(5) << endl; //1

	itree._M_insert_equal(5);
	itree._M_insert_equal(5);
	cout << itree.size() << endl;   //7, since using insert_equal().
	cout << itree.count(5) << endl; //3    
}