在数据驱动的时代，机器学习算法以其强大的数据处理和分析能力，成为推动各行各业智能化发展的关键引擎。其中，分类与预测算法更是机器学习的核心所在，它们不仅能够帮助我们理解数据的内在规律，还能为未来的决策提供有力支持。然而，仅仅实现算法的功能并不足够，对算法性能进行准确评价和优化同样至关重要。本文将通过实例和代码，深入探讨分类算法评价方式中的F1值和P-R曲线，以及它们在实际应用中的意义。

一、分类算法与性能评价的重要性

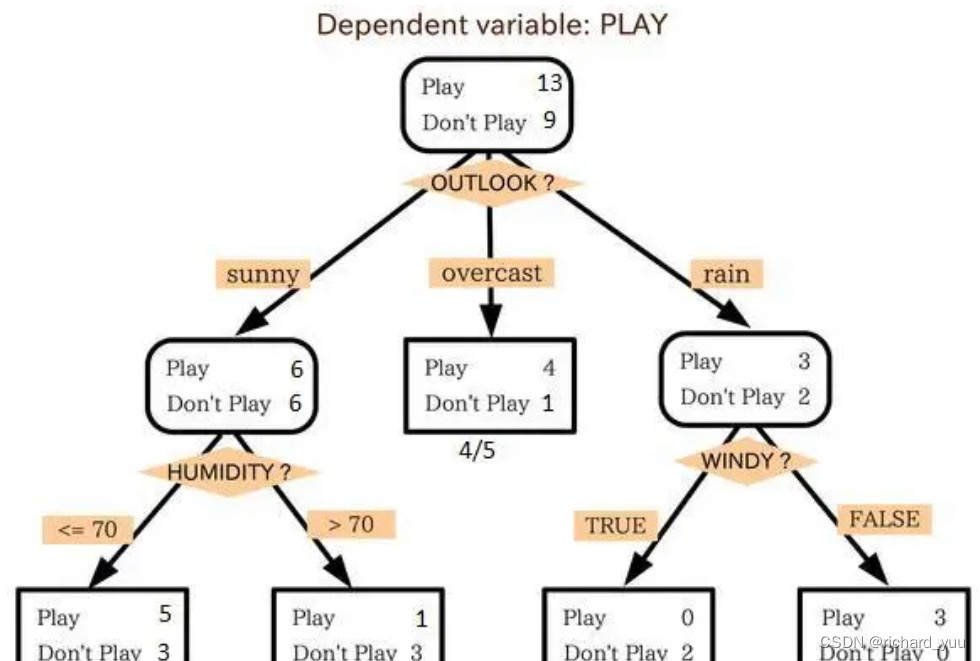
分类算法，如支持向量机、决策树、随机森林等，是机器学习领域的基石。它们能够基于数据的特征，自动将数据划分为不同的类别，从而实现数据的自动化、智能化处理。然而，不同的分类算法在处理相同问题时，其性能往往会有所差异。因此，我们需要对算法的性能进行评价，以选择最适合当前任务的算法，并为其后续的优化提供方向。

二、F1值与P-R曲线的概念与意义

在评价分类算法的性能时，准确率、精确率、召回率以及F1值等指标都是常用的评价标准。其中，F1值是精确率和召回率的调和平均值，它能够综合考虑这两个指标，从而更全面地评价算法的性能。而P-R曲线则是以召回率为横轴，精确率为纵轴绘制的曲线，它能够直观地展示算法在不同阈值下的性能表现。

三、实例解析：以垃圾邮件检测为例

为了更好地理解F1值和P-R曲线的应用，我们以垃圾邮件检测为例进行解析。假设我们有一个垃圾邮件检测算法，其任务是将邮件划分为“垃圾邮件”和“正常邮件”两个类别。我们可以通过以下步骤来评价和优化该算法的性能。
首先，我们需要收集一组带有标签的邮件数据，其中标签表示邮件是否为垃圾邮件。然后，我们使用算法对这批数据进行分类，并计算得到精确率、召回率和F1值等指标。假设我们得到的结果如下：
精确率：0.9
召回率：0.8
F1值：0.85
接下来，我们可以绘制P-R曲线来进一步分析算法的性能。通过调整分类阈值，我们可以得到一系列不同的精确率和召回率组合，并将它们绘制在P-R曲线上。通过观察曲线的形状和位置，我们可以判断算法在不同召回率下的精确率表现。如果曲线靠近右上角，说明算法的性能较好；如果曲线较为平缓或靠近坐标轴，则说明算法的性能较差。
基于P-R曲线的分析结果，我们可以对算法进行进一步优化。例如，如果我们发现算法在召回率较低时精确率较高，而在召回率较高时精确率急剧下降，那么我们可以尝试调整算法的参数或采用其他更复杂的模型来提高召回率，同时保持较高的精确率。

四、代码实现与结果分析

在实际应用中，我们可以使用Python等编程语言来实现上述评价和优化过程。以下是一个简单的示例代码，用于计算精确率、召回率和F1值，并绘制P-R曲线：

python

from sklearn.metrics import precision_recall_curve, auc, f1_score
import matplotlib.pyplot as plt

# 假设y_true是真实的标签，y_scores是算法预测的概率值
y_true = [0, 0, 1, 1, 1]
y_scores = [0.1, 0.4, 0.35, 0.8, 0.9]

# 计算精确率和召回率
precision, recall, thresholds = precision_recall_curve(y_true, y_scores)

# 计算F1值
f1 = f1_score(y_true, (y_scores > 0.5).astype(int))

# 绘制P-R曲线
plt.plot(recall, precision, color='b', label='P-R Curve')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.ylim([0.0, 1.05])
plt.xlim([0.0, 1.0])
plt.title('Precision-Recall Curve')
plt.legend(loc="lower left")
plt.show()

# 输出F1值
print(f"F1 Score: {f1}")

通过运行上述代码，我们可以得到F1值和P-R曲线的可视化结果。根据这些结果，我们可以对算法的性能进行定性和定量的评估，并为后续的优化工作提供指导。

五、结论与展望

本文通过对F1值和P-R曲线的深入解析，展示了它们在机器学习分类算法评价与优化中的重要作用。通过实例和代码的实现，我们更加直观地理解了这些评价指标的计算方法和应用场景。未来，随着机器学习技术的不断发展，我们期待有更多的评价指标和优化方法被提出，以进一步提高分类与预测算法的性能和稳定性。