前向传播、反向传播教程：包含梯度计算理解
前馈神经网络：

• 前向传播：输入信号 输入模型计算 得到输出的过程
• 反向传播：将损失的梯度回传，传播误差，从而更新每层权重参数的过程。本质上是利用（求导的）链式法则，计算损失函数对所有参数的梯度。
  • $新的权重=旧的权重-学习率\times 梯度$

一、自动微分简单介绍

  在 PyTorch 中，张量的自动微分功能是通过一个叫做自动微分（Automatic Differentiation，简称 AD）的系统实现的。自动微分是一种用于自动计算导数的技术，它在机器学习和深度学习中扮演着核心角色，特别是在神经网络的训练过程中计算梯度时。

1、基本原理

  在 PyTorch 中，每个 torch.Tensor 对象都有一个 requires_grad 属性；如果设置为 True，PyTorch 会跟踪所有对该张量的操作。当完成计算后，你可以调用 .backward() 来自动计算所有梯度，这些梯度会累积到相应张量的 .grad 属性中。

2、梯度计算过程

当你对一个输出张量执行 .backward() 时，PyTorch 会进行如下步骤：

1. 反向传播：从输出张量开始，反向遍历整个操作图（计算图），计算每个节点的梯度。
2. 链式法则：自动应用链式法则计算梯度。
3. 累积梯度：对于那些有多个子节点的张量（在图中被多次引用），梯度会累积，而不是被替换。

3、示例：基于 PyTorch 的自动微分

让我们通过一个简单的例子来看看 PyTorch 如何实现自动微分：

import torch

# 创建一个张量，并设置requires_grad=True来追踪与它相关的计算
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
# x = torch.tensor([1.0, 2.0, 3.0])
# x.requires_grad=True
# 是一样的

# 定义张量上的操作
y = x * x  # y = x^2 ，逐元素乘法得 tensor[1.0,4.0,9.0]
z = y.mean()  # z = 1/3 * sum(x^2)

# 计算z关于x的梯度
z.backward()

# 打印梯度 dz/dx
print(x.grad)

逐元素乘法：张量的基础运算
在这个例子中，x 是一个具有三个元素的张量，我们对它应用平方操作得到 y，然后对 y 取均值得到 z。调用 z.backward() 后，x 的梯度将存储在 x.grad 中。

输出将是：

tensor([0.6667, 1.3333, 2.0000])

这个梯度实际上是函数 $z=\frac{1}{3}\sum x^2$ 在 $x=[1.0,2.0,3.0]$ 处的导数。

在 梯度下降法 反向传播中，如果 x 是模型中的一个可训练的权重参数，并且我们已经计算出了损失函数关于 x 的梯度（x.grad），那么在权重更新阶段，x 会按照以下方式更新：
$$x\leftarrow x-\text{学习率}\times x.\text{grad}$$
在梯度上升法中 区别是加号。

a.示例详解

示例包括以下步骤：

1. 张量创建：x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
2. 应用操作：y = x * x (即 $y=x^2$)
3. 计算均值：z = y.mean() (即 $z=\frac{1}{3}\sum x^2$)

当我们调用 z.backward() 时，计算图会反向传递梯度，使用链式法则计算关于每个节点的梯度。

b.梯度计算过程

1. 初始化：梯度 dz/dz 初始化为 1。
2. 从 z 到 y：应用链式法则，计算 dz/dy。由于 $z=\frac{1}{3}\sum y$，有 dz/dy = [1/3, 1/3, 1/3]。
3. 从 y 到 x：继续使用链式法则，计算 dy/dx。由于 y = x^2，有 dy/dx = 2x。所以在 x = [1.0, 2.0, 3.0] 处，我们得到 dy/dx = [2*1.0, 2*2.0, 2*3.0] = [2, 4, 6]。
4. 组合：结合这些，得到 dz/dx = dz/dy * dy/dx = [1/3, 1/3, 1/3] * [2, 4, 6] = [2/3, 4/3, 6/3] = [0.6667, 1.3333, 2.0000]。

c.可视化计算图

import torchviz
import torch
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
y = x * x
z = y.mean()
z.backward()

torchviz.make_dot(z, params={'x': x, 'y': y, 'z': z})

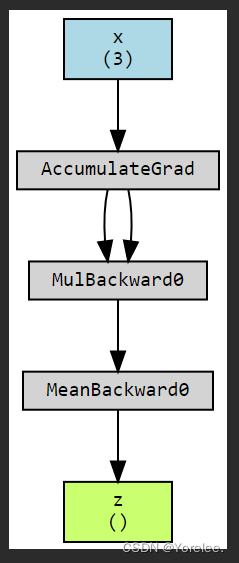
安装 Graphviz

• x (3): 这是一个有 3 个元素的一维张量 [1.0, 2.0, 3.0]，作为计算图的输入。它的形状是$(3)$，代表有 3 个元素。

• AccumulateGrad: 这表示梯度累积节点。由于 x 被创建为 requires_grad=True，所以 PyTorch 会追踪它的梯度。当 z.backward() 被调用时，PyTorch 会计算 z 相对于 x 的梯度，并将这些梯度累积（即累加）到 x 的 .grad 属性中。

• MulBackward0: 这是一个反向传播操作，表示 y = x * x 操作的梯度计算。MulBackward0 是 PyTorch 自动为乘法操作分配的反向传播函数。

• MeanBackward0: 类似地，这是 z = y.mean() 的反向传播操作。MeanBackward0 计算 z 相对于 y 的梯度。

• z (): 这是计算图的最终输出。z 是 y 张量的平均值。由于 z 是一个标量（即它只有一个元素），所以它的形状为空（()）。

箭头显示了数据和梯度的流向。当调用 z.backward() 时，PyTorch 会沿着这些箭头的方向逆向传播梯度，从 z 开始，通过 MeanBackward0 和 MulBackward0，最后到达 x 并在 AccumulateGrad 节点处累积梯度。

4、总结

总的来说，一般输出通过最终的损失函数来反向计算梯度。梯度实际上就是进行链式法则求偏导得到对应点的值，这个梯度可以根据学习率大小用来更新权重。

以上的实际上，我们可以把z看作 损失函数（不管意义是啥），x看作可训练的权重参数，然后反向传播z对x求梯度，最后得到了每个x值的梯度值（求法在之前有介绍，就是一个链式法则求某个点的导数而已），然后更新x，可以简略认为是一个神经网络的反向传播过程。
$$损失函数：z=\frac{1}{3}\sum x^2$$
$$反向传播更新：x\leftarrow x-\text{学习率}\times x.\text{grad}$$

二、为什么要计算损失，为何权重更新是对的？

我们从梯度下降来理解~

1、梯度下降数学原理

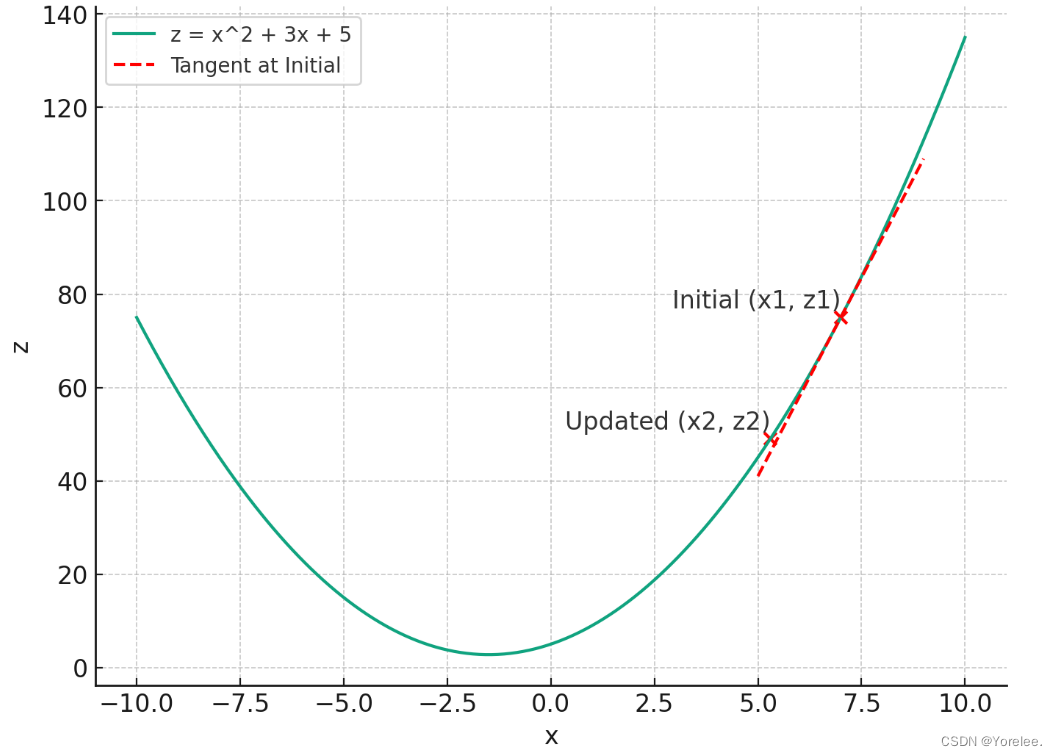
  我们说对一个权重求梯度，实际上就是目标函数z对该权重求偏导，而链式法则也不过是一个求导方法，最后不过也相当于把其他变量看成常数，对需要求导的变量进行求导。对x求偏导可以把其他变量（其他权重）看作一个常数。换句话说，我们先理解成，z关于x的单变量函数，因此我们对x求梯度之后（即导数之后），根据导数的下降方向改变原来的x，实际上这个变化后x值就可以使得z值更小。因此我们所谓的梯度下降，实际上就是通过对x求偏导沿z下降的方向更新x， 使得z（损失函数）更小的方法。

• 沿梯度方向下降更新权重，实际上就是可以看成z=z(x)，让z最小，对x求导，让x沿梯度下降的方向变化，达到z变小的目的。

  而我们的学习率（通常表示为 $\alpha$ 或 $\eta$ 在梯度下降算法中扮演着关键的角色，因为它决定了每一步更新参数时的步长：

1. 学习率过大：

   • 如果学习率设置得太大，那么每次更新时步长过长，可能会导致参数 (x) 跳过最小值点，甚至可能导致每次迭代后离最小值点越来越远，从而使算法发散，无法收敛到最小值。

2. 学习率过小：

   • 反之，如果学习率太小，虽然可以保证更稳定地逼近最小值，但更新的速度会非常慢。这不仅意味着需要更多的迭代次数才能达到最小值，而且还可能在到达全局最小值前就因为其他条件（如迭代次数限制或计算时间限制）而停止，导致算法效率低下。

3. 梯度为零的情况：

   • 理想情况下，当达到函数的最小值点时，该点的梯度为零。在这种情况下，由于没有梯度（即没有变化的方向或大小），参数不再更新，算法停止。这是梯度下降算法收敛的标志。

合适的学习率选择对于梯度下降法的成功至关重要。在实践中，选择合适的学习率可能需要基于经验、实验调整或者使用一些适应性学习率调整策略，如 Adam 或 AdaGrad，这些方法可以自动调整学习率，以改进梯度下降的性能和稳定性。

2、梯度上升

刚刚提到的梯度下降让损失函数达到最小值，那么梯度上升就是反过来了，它让目标函数达到最大值。

三、在模型中使用自动微分

import torch


class MyModel(torch.nn.Module):
    def __init__(self):
        super(MyModel, self).__init__()

    def forward(self, x, w, b):
        return 1 / (torch.exp(-(w * x + b)) + 1)


model = MyModel()

# 设置输入参数
x = torch.tensor(1.0, requires_grad=True)
w = torch.tensor(0.0, requires_grad=True)
b = torch.tensor(0.0, requires_grad=True)

# Forward pass
output = model(x, w, b)

# Backward pass
output.backward()

# Access the gradients
print(x.grad)  # Gradient with respect to x
print(w.grad)  # Gradient with respect to w
print(b.grad)  # Gradient with respect to b

使用 PyTorch 中的 backward() 方法可以自动计算所有注册了梯度（即设置了 requires_grad=True）的张量的导数。在示例中，x, w, 和 b 都被设置为 requires_grad=True，这意味着 PyTorch 会追踪这些变量的所有操作，用来构建一个计算图。当调用 output.backward() 时，PyTorch 将自动计算 output 对于所有涉及的变量的梯度。

模型执行的是逻辑回归的前向传播公式：

$$\text{output}=\frac{1}{\exp (-(w\cdot x+b))+1}$$

这是一个经典的 sigmoid 激活函数应用。以下是 backward() 过程的详细说明：

1. 前向传播（Forward Pass）：
   在前向传播中，使用给定的输入 x, w, 和 b，按照您定义的 forward 方法计算输出。

2. 反向传播（Backward Pass）：
   当 output.backward() 被调用时，PyTorch 从 output 开始，自动计算它对 x, w, 和 b 的梯度。这是通过反向遍历从输出到每个输入的计算图，应用链式法则完成的。

3. 访问梯度：
   在反向传播之后，每个变量的 .grad 属性会包含其对应的梯度。这些梯度表示了损失函数相对于每个变量在当前值的斜率或变化率。

• x.grad 会包含 output 对 x 的梯度。
• w.grad 会包含 output 对 w 的梯度。
• b.grad 会包含 output 对 b 的梯度。

这些梯度可以用于优化步骤，比如在一个训练循环中用梯度下降法更新 w 和 b。这是实现参数更新和模型训练的关键步骤。