三维空间中散点平面拟合方法

news2025/1/19 3:28:06

1、三点求平面方程、平面法向量和点到平面的距离
已知三点p1（x1,y1,z1），p2(x2,y2,z2)，p3(x3,y3,z3)，

要求确定的平面方程,关键在于求出平面的一个法向量

为此做向量p1p2（x2-x1,y2-y1,z2-z1), p1p3(x3-x1,y3-y1,z3-z1),平面法线和这两个向量垂直，因此法向量n：
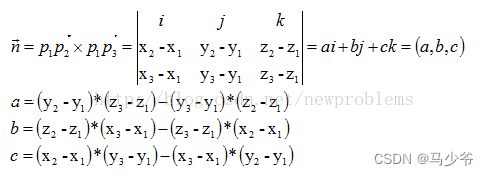
在这里插入图片描述
平面方程：a(x-x1)+b(y-y1)+ c(z-z1)=0；

d=-ax1-by1-c*z1。
平面平面方程为 ax+by+cz+d=0。

//已知3点坐标，求平面ax+by+cz+d=0;
 
void get_panel(Point p1,Point p2,Point p3,double &a,double &b,double &c,double &d)
 
{
 
    a = (p2.y - p1.y)*(p3.z - p1.z) - (p2.z - p1.z)*(p3.y - p1.y);
 
    b = (p2.z - p1.z)*(p3.x - p1.x) - (p2.x - p1.x)*(p3.z - p1.z);
 
    c = (p2.x - p1.x)*(p3.y - p1.y) - (p2.y - p1.y)*(p3.x - p1.x);
 
    d = 0 - (a * p1.x + b*p1.y + c*p1.z);
 
}
 
 
// 已知三点坐标，求法向量
 
Vec3 get_Normal(Point p1,Point p2,Point p3)
 
{
 
    a = (p2.y - p1.y)*(p3.z - p1.z) - (p2.z - p1.z)*(p3.y - p1.y);
 
    b = (p2.z - p1.z)*(p3.x - p1.x) - (p2.x - p1.x)*(p3.z - p1.z);
 
    c = (p2.x - p1.x)*(p3.y - p1.y) - (p2.y - p1.y)*(p3.x - p1.x);
 
    return Vec3(a, b, c);
 
}
 
 
//点到平面距离
 
double dis_pt2panel(Point pt,double a,double b,double c,double d)
{
 
    return f_abs(a * pt.x + b*pt.y + c*pt.z + d) / sqrt(a * a + b * b + c * c);
 
}

设空间中一组带噪声的位于某个平面的散点 $x_{i},y_{i},z_{i}),i=1,2,...,N，$ 对于平面方程的一般表达式 $A x + B y + C z + D = 0$ ，对于不过原点的平面有 $A x + B y + C z + 1 = 0$ ，于是问题就变成了求系数A，B，C使得散点尽可能的落在该平面上。下面笔者将从两种角度来推导最小二乘下的最优解。

求误差函数的极小值点的方法
设A，B，C为平面的最优参数，则对于每个点 $x_{i},y_{i},z_{i}),i=1,2,...,N$ 带人该平面表达式中存在误差 $e_{i}=Ax_{i}+By_{i}+Cz_{i}+1$ ，我们将所有的误差的平方进行求和则有：
设A，B，C为平面的最优参数，则对于每个点带人该平面表达式中存在误差，我们将所有的误差的平方进行求和则有：
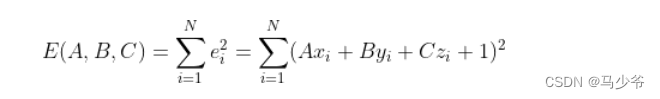
在这里插入图片描述
可见误差的平方和为A,B,C的函数，我们通过观察可以很容易的发现该函数是4维空间中的一个下凸超平面，且具有唯一的极小值，同时也是全局最小值。那么E对A,B,C的一阶偏导都为0，即：

展开整理可得：
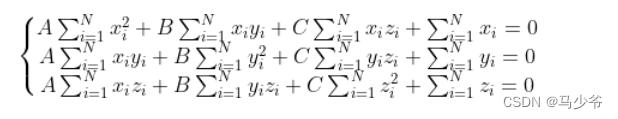
在这里插入图片描述
我们令： $\bar{x}=\frac{1}{N}\sum_{i=1}^{N}x_{i}，\bar{y}=\frac{1}{N}\sum_{i=1}^{N}y_{i}，\bar{z}=\frac{1}{N}\sum_{i=1}^{N}z_{i}，\bar{x^{2}}=\frac{1}{N}\sum_{i=1}^{N}x_{i}^{2},\bar{y^{2}}=\frac{1}{N}\sum_{i=1}^{N}y_{i}^{2},\bar{z^{2}}=\frac{1}{N}\sum_{i=1}^{N}z_{i}^{2}，\bar{xy}=\frac{1}{N}\sum_{i=1}^{N}x_{i}y_{i}，\bar{xz}=\frac{1}{N}\sum_{i=1}^{N}x_{i}z_{i}，\bar{yz}=\frac{1}{N}\sum_{i=1}^{N}y_{i}z_{i}$ 则（3）可以被写成如下形式：
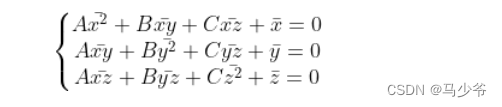
在这里插入图片描述
可以看到（4）就是一个3元一次方程组，求解这个方程组就可以得到A,B,C的值。

几何的方法
下面来介绍如何使用几何的方法来进行推导，我们令
$X=\begin{bmatrix} x_{1}\\ x_{2}\\ ...\\ x_{N} \end{bmatrix}，{X}'=\begin{bmatrix} -1-By_{1}-Cz_{1}\\ -1-By_{2}-Cz_{2}\\ ...\\ -1-By_{N}-Cz_{N} \end{bmatrix}$

现在的问题是找到合适的参数A使得AX最接近{X}‘，它们的误差向量为AX-{X}’，从几何的角度来看当误差向量AX-{X}'与X正交时有最优系数，即
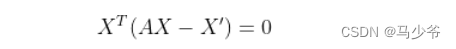
在这里插入图片描述
将(5)展开可得：

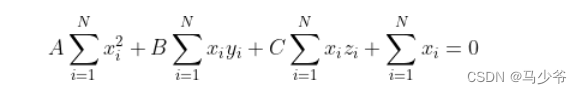
可以看到（6）式即为（3）中的第一项。
我们分别令
$Y=\begin{bmatrix} y_{1}\\ y_{2}\\ ...\\ y_{N} \end{bmatrix}，{Y}'=\begin{bmatrix} -1-Ax_{1}-Cz_{1}\\ -1-Ax_{2}-Cz_{2}\\ ...\\ -1-Ax_{N}-Cz_{N} \end{bmatrix}，Z=\begin{bmatrix} z_{1}\\ z_{2}\\ ...\\ z_{N} \end{bmatrix}，{Z}'=\begin{bmatrix} -1-Ax_{1}-By_{1}\\ -1-Ax_{2}-By_{2}\\ ...\\ -1-Ax_{N}-By_{N} \end{bmatrix}，同样地我们有：Y^{T}(BY-{Y}')=0，Z^{T}(CZ-{Z}')=0$ ，展开后发现它们分别是式（3）中的第2和第3项。