独木桥
题目背景
战争已经进入到紧要时间。你是运输小队长,正在率领运输部队向前线运送物资。运输任务像做题一样的无聊。你希望找些刺激,于是命令你的士兵们到前方的一座独木桥上欣赏风景,而你留在桥下欣赏士兵们。士兵们十分愤怒,因为这座独木桥十分狭窄,只能容纳 1 1 1 个人通过。假如有 2 2 2 个人相向而行在桥上相遇,那么他们 2 2 2 个人将无法绕过对方,只能有 1 1 1 个人回头下桥,让另一个人先通过。但是,可以有多个人同时呆在同一个位置。
题目描述
突然,你收到从指挥部发来的信息,敌军的轰炸机正朝着你所在的独木桥飞来!为了安全,你的部队必须撤下独木桥。独木桥的长度为 L L L,士兵们只能呆在坐标为整数的地方。所有士兵的速度都为 1 1 1,但一个士兵某一时刻来到了坐标为 0 0 0 或 L + 1 L+1 L+1 的位置,他就离开了独木桥。
每个士兵都有一个初始面对的方向,他们会以匀速朝着这个方向行走,中途不会自己改变方向。但是,如果两个士兵面对面相遇,他们无法彼此通过对方,于是就分别转身,继续行走。转身不需要任何的时间。
由于先前的愤怒,你已不能控制你的士兵。甚至,你连每个士兵初始面对的方向都不知道。因此,你想要知道你的部队最少需要多少时间就可能全部撤离独木桥。另外,总部也在安排阻拦敌人的进攻,因此你还需要知道你的部队最多需要多少时间才能全部撤离独木桥。
输入格式
第一行共一个整数 L L L,表示独木桥的长度。桥上的坐标为 1 , 2 , ⋯ , L 1, 2, \cdots, L 1,2,⋯,L。
第二行共一个整数 N N N,表示初始时留在桥上的士兵数目。
第三行共有 N N N 个整数,分别表示每个士兵的初始坐标。
输出格式
共一行,输出 2 2 2 个整数,分别表示部队撤离独木桥的最小时间和最大时间。 2 2 2 个整数由一个空格符分开。
样例 #1
样例输入 #1
4
2
1 3
样例输出 #1
2 4
提示
对于 100 % 100\% 100% 的数据,满足初始时,没有两个士兵同在一个坐标, 1 ≤ L ≤ 5 × 1 0 3 1\le L\le5\times 10^3 1≤L≤5×103, 0 ≤ N ≤ 5 × 1 0 3 0\le N\le5\times10^3 0≤N≤5×103,且数据保证 N ≤ L N\le L N≤L。
在做这道题的时候思路走偏了,导致想用找规律的方法来解决这道题,最后当然是不对的。
首先对于两个迎面而走的士兵,会有如图所示的走法:
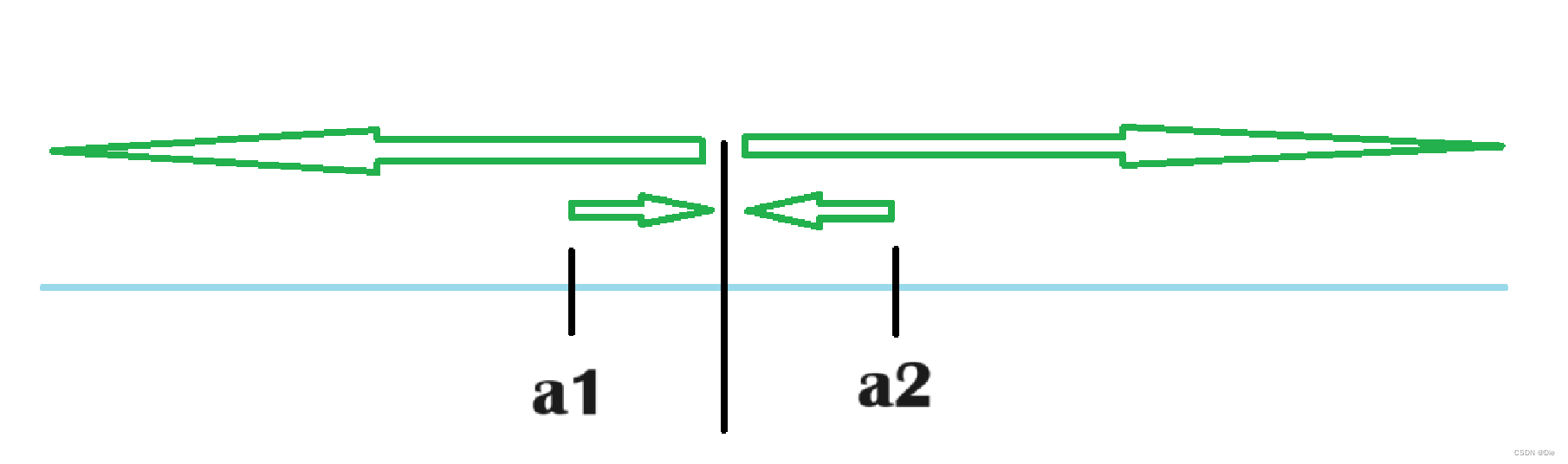
所以就相当于a2和a1擦肩而过,然后a2走a2的,a1走a1的一样。
也就是说我们不必考虑每两个士兵会在什么时候什么地点相遇。
在求解第一问最小时间的时候,我们只需要让所有士兵去找左右两端更近的那一边走就可以了,因为就算相撞也是擦肩而过。
那么最终得到的最长时间就是花费时间最长的那个士兵走到头所需要的时间,所以可以直接枚举所有士兵,先对他们向左和向右的时间花费取最小值,然后再从全局取所有最小值的最大值。
在求解第二问的时候,可以对所有士兵的坐标进行排序,最靠左的就让他向右走,最靠右的就让他向左走,然后在他们两个中间取最大值,这样就能够求解出时间最大值。
CODE:
#include<bits/stdc++.h>
using namespace std;
const int N = 5e3+10;
int a[N];
int main(){
int l,n;
cin >> l >> n;
for(int i = 1;i <= n;i++){
cin >> a[i];
}
if(n == 0){ //特判
cout << 0 << " " << 0 << endl;
return 0;
}
if(n == 1){
cout << min(a[1],l-a[1]+1) << " " << max(a[1],l - a[1] + 1);
return 0;
}
int res = -1e9;
for(int i = 1;i <= n;i++){
res = max(res,min(a[i],l - a[i] + 1));
}
cout << res << " ";
sort(a+1,a+1+n);
res = max(a[n],l - a[1] + 1);
cout << res << endl;
return 0;
}

![下列程序定义了NxN的二维数组,并在主函数中自动赋值。请编写函数fun(int a[][N],int n),该函数的功能是:使数组右上半三角元素中的值乘以m。](https://img-blog.csdnimg.cn/direct/810d3107b3ec45bc8500a4afedf90d0e.png)