双线性插值计算手动实现以及原理
- 代码
- 原理
代码
先贴代码吧,原理其实也比较简单,看代码基本也就理解了,时间太晚了,原理后续再补吧。
import torch
from torch.nn import functional as F
import numpy as np
from itertools import product
import warnings
warnings.filterwarnings('ignore')
def data_gen(in_wh,out_wh):
in_w,in_h = in_wh
out_w,out_h = out_wh
inp = torch.range(0,in_h*in_w-1,1).reshape(1,1,in_h, in_w)
new_h = torch.linspace(-1, 1, out_h).view(-1, 1).repeat(1, out_w)
new_w = torch.linspace(-1, 1, out_w).repeat(out_h, 1)
grid = torch.cat((new_w.unsqueeze(2), new_h.unsqueeze(2)), dim=2)#+2/5
# print(grid.shape)
grid = grid.unsqueeze(0).clip(-1,1)
return inp,grid
def torch_interp(in_wh,out_wh):
'''torch 插值'''
inp,grid = data_gen(in_wh,out_wh)
print(inp)
outp = F.grid_sample(inp, grid=grid, align_corners=True)
# print(outp)
return outp
def my_interp(in_wh,out_wh):
'''手动实现的插值计算'''
inp,grid = data_gen(in_wh,out_wh)
in_w,in_h = in_wh
p_h = 2/(in_h-1)#计算h方向上每一份的长度
p_w = 2/(in_w-1)#计算w方向上每一份的长度
p_ = np.array([p_w,p_h])#合并
inp = inp[0,0,:,:]
grid = grid[0]
out = np.zeros((grid.shape[0],grid.shape[1]))#初始化输出模板
for (_i,_j) in product(range(grid.shape[0]),range(grid.shape[1])):
maps = (grid[_i,_j]).cpu().numpy()
interp_start = (maps+1)//p_#计算插值的起始点
offset = (maps+1)%p_#计算距离起始点的偏移量
interp_start = interp_start.astype(np.int32)
# print(interp_start)
w, pix = [], []
for j,i in [(0,0),(0,1),(1,0),(1,1)]:
w.append(abs((i*p_[0]-offset[0])*(p_[1]*j-offset[1]))/(p_[0]*p_[1]))#双线性插值的面积计算
interp_start_ = interp_start+np.array([i,j])#计算插值的四个点中的某一个
interp_start_[0]=interp_start_[0].clip(0,in_w-1)#控制不超出原图像边界
interp_start_[1]=interp_start_[1].clip(0,in_h-1)
pix.append(inp[interp_start_[1]][interp_start_[0]])
w = np.array(w)
pix = np.array(pix[::-1])
interp_val = round((w*pix).sum(),3)
out[_i,_j]=interp_val
return out
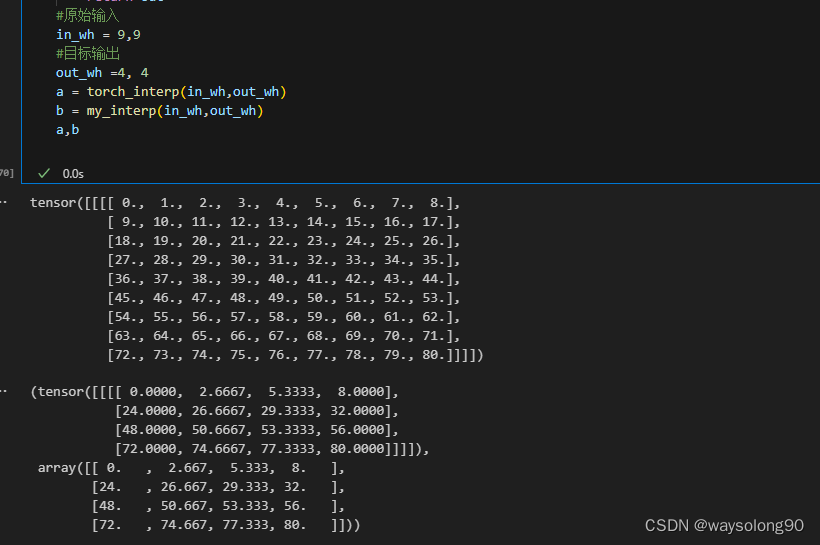
#原始输入
in_wh = 9, 9
#目标输出
out_wh =5, 2
a = torch_interp(in_wh,out_wh)
b = my_interp(in_wh,out_wh)
print(a,b)
结果:
tensor([[[[ 0., 1., 2., 3., 4., 5., 6., 7., 8.],
[ 9., 10., 11., 12., 13., 14., 15., 16., 17.],
[18., 19., 20., 21., 22., 23., 24., 25., 26.],
[27., 28., 29., 30., 31., 32., 33., 34., 35.],
[36., 37., 38., 39., 40., 41., 42., 43., 44.],
[45., 46., 47., 48., 49., 50., 51., 52., 53.],
[54., 55., 56., 57., 58., 59., 60., 61., 62.],
[63., 64., 65., 66., 67., 68., 69., 70., 71.],
[72., 73., 74., 75., 76., 77., 78., 79., 80.]]]])
(tensor([[[[ 0., 2., 4., 6., 8.],
[72., 74., 76., 78., 80.]]]]),
array([[ 0., 2., 4., 6., 8.],
[72., 74., 76., 78., 80.]]))
自己试了几组数据,结果均与torch一致。
原理
先简要说一下原理吧
在线性插值的情况下:
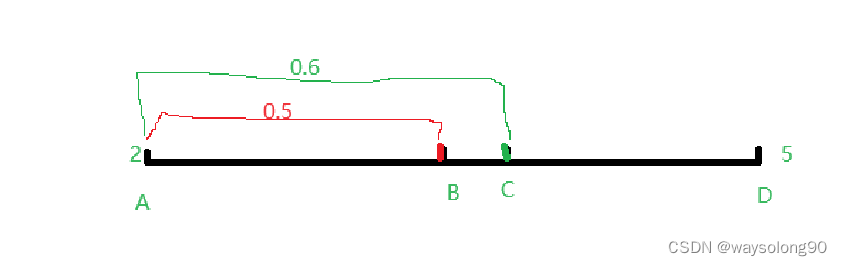
假设AB=AD/2,那么B的坐标等于(1-0.5)×A+0.5×D= 3.5
那么C点坐标等于(1-0.6)×A+0.6×D=3.8
那么在双线性插值的情况下,
增加了一个维度
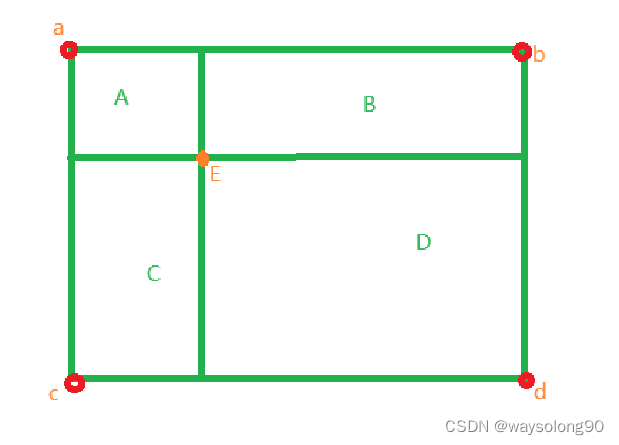
E的像素值等于e = (D×a+B×c+A×d+C×b)/(A+B+C+D)
其中ABCD表示对应区域的面积

![下列程序定义了NxN的二维数组,并在主函数中自动赋值。请编写函数fun(int a[][N],int n),该函数的功能是:使数组右上半三角元素中的值乘以m。](https://img-blog.csdnimg.cn/direct/810d3107b3ec45bc8500a4afedf90d0e.png)