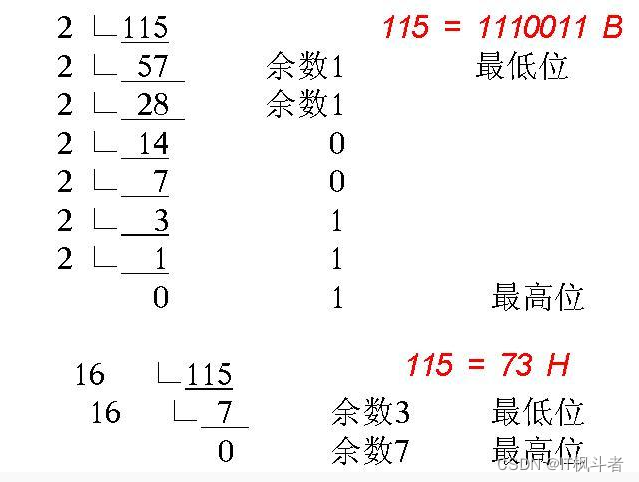
哈希表的基本思路是通过某种方式将某个值映射到对应的位置，这里的采取的方式是除留余数法，即将原本的值取模以后再存入到数组的对应下标，即便存入的值是一个字符串，也可以根据字符串哈希算法将字符串转换成对应的ASCII码值，然后再取模。

如果某个位置已经存了其他数据，那么就需要找一个空闲位置来存放当前数据，我们把这种方式称为闭散列（或者开放地址法）。

---

         目录

1、线性探测法

(1) 基本思路

(2) 哈希表数据存储结构

(3) 查找实现

(4) 插入实现

(5) 移除实现

2、二次探测法

3、细节处理：遇到string或者自定义类型如何处理

---

1、线性探测法

(1) 基本思路

如果当前位置已经存了其他数据，那就看下一个位置是否空着，如果空着就存，被占了就继续看下一个位置，每次检索的步长为1，这种方式检索方式称为“线性探测法”。

假设第 start 个位置已经存了其他数据，那么后续检索的位置是 start + i，i = 0,1,2 ...

(2) 哈希表数据存储结构

哈希表每个位置可以只存一个数据，也可以存键值对，除此之外，还需要加一个状态标记。以查找为例，查找时，一般是遇到空就停下来，如果在找到某个数之前就遇到了空，就会导致后面的数据遍历不到；如果全部遍历一遍，效率太低。

因此，我们可以为表中的每个数据添加状态标记，只要不是 EMPTY 状态，就一直搜索。

enum Status
{
    EXIST,
    EMPTY,
    DELETE
};

template <class K, class V>
struct HashData
{
    pair<K, V> _kv;
    Status _status = EMPTY;     // 初始化缺省为 EMPTY
};

(3) 查找实现

HashData<K, V> *Find(const K &key)
{
    if (_tables.size() == 0)
    {
        return nullptr;
    }

    HashFunc hf;
    size_t start = hf(key) % _tables.size();    // 这里的 size() 是哈希表的有效数据个数
    size_t i = 0;
    size_t index = start;
    // 线性探测 or 二次探测
    while (_tables[index]._status != EMPTY)
    {
        if (_tables[index]._kv.first == key && _tables[index]._status == EXIST)
        {
            return &_tables[index];
        }

        ++i;
        
        index = start + i;        // 改为二次探测：index = start + i*i;

        index %= _tables.size();    // 避免超出哈希表的容量范围
    }

    return nullptr;
}

(4) 插入实现

插入实现时有两点需要额外注意：

• 检查插入内容是否存在。这样做的目的是为了去重
• 检查是否需要扩容。随着哈希表中数据个数的增加，哈希碰撞的次数也会增加，为了缓解哈希碰撞，当哈希表中有效数据个数达到 哈希表容量的 70% 以后，需要将哈希表扩容，并将原表的数据重新取模映射到新表。

bool Insert(const pair<K, V> &kv)
{
    // 判断插入内容是否存在
    HashData<K, V> *ret = Find(kv.first);
    if (ret)
    {
        return false;
    }

    // 负载因子到0.7，就扩容
    if (_tables.size() == 0 || _n * 10 / _tables.size() >= 7)
    {
        // 扩容
        size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
        HashTable<K, V, HashFunc> newHT;
        newHT._tables.resize(newSize);
        
        // 非递归排布：遍历原表，把原表中的数据，重新按newSize映射到新表
        //vector<HashData<K, V>> newTables;
		//newTables.resize(newSize);
		//for (size_t i = 0; i < _tables.size(); ++i)
		//{
		//	
		//}
		//_tables.swap(newTables);

        // 递归排布
        for (size_t i = 0; i < _tables.size(); ++i)
        {
            if (_tables[i]._status == EXIST)
            {
                newHT.Insert(_tables[i]._kv);
            }
        }

        _tables.swap(newHT._tables);
    }

    HashFunc hf;
    size_t start = hf(kv.first) % _tables.size();
    size_t i = 0;
    size_t index = start;
    // 线性探测 or 二次探测
    while (_tables[index]._status == EXIST)
    {
        ++i;
        index = start + i;            // 改为二次探测：index = start + i*i;

        index %= _tables.size();
    }

    _tables[index]._kv = kv;
    _tables[index]._status = EXIST;
    ++_n;

    return true;
}

(5) 移除实现

bool Erase(const K &key)
{
    HashData<K, V> *ret = Find(key);
    if (ret == nullptr)
    {
        return false;
    }
    else
    {
        --_n;                     // 有效数据个数减1
        ret->_status = DELETE;    // 状态标记设为 DELETE（插入时遇到DELETE表示该位置可以存数据）
        return true;
    }
}

2、二次探测法

这里的二次指的是 二次方

• 线性探测法每次检索的步长是1，检索的位置：start + i，i = 0,1,2 ...，
• 二次探测法每次检索的步长不固定，每次检索的位置：start + i^2，i = 0,1,2 ...

二次线性探测法没有从根本上解决线性探测法的问题，只是不会让数据分布过于紧密。二次线性探测法的模拟实现只需要在线性探测法的基础上修改一处即可。

3、细节处理：遇到string或者自定义类型如何处理

如果哈希表中保存的数据类型是 string 或者 自定义结构体类型，按照上面这种逻辑，肯定会报错，但是我们可以使用仿函数来处理。下面以字符串的处理为例。

template<class K>
struct Hash
{
	size_t operator()(const K& key)
	{
		return key;        // 如果是内置类型(说明可以自己强转成整型)，直接返回
	}
};

// 特化：如果传入的是字符串，就会调用模板特化处理
template<>
struct Hash < string >
{
	size_t operator()(const string& s)
	{
		// BKDR字符串哈希算法: 字符串中的每个字符的ASCII码值先乘以31 再加上 之前的值          
		size_t value = 0;
		for (auto ch : s)
		{
			value *= 31;
			value += ch;
		}
		return value;
	}
};