神经网络的构建

import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
    return 1/(1+np.exp(-x))
def identity_function(x):#恒等函数
    return x
def init_network():#进行权重和偏置的初始化，并保存到字典中
    network={}
    network['W1']=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
    network['b1']=np.array([0.1,0.2,0.3])
    network['W2']=np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
    network['b2']=np.array([0.1,0.2])
    network['W3']=np.array([[0.1,0.3],[0.2,0.4]])
    network['b3']=np.array([0.1,0.2])

    return network

def forward(network,x):#输入到输出的处理
    W1,W2,W3=network['W1'],network['W2'],network['W3']
    b1,b2,b3=network['b1'],network['b2'],network['b3']

    a1=np.dot(x,W1)+b1
    z1=sigmoid(a1)
    a2=np.dot(z1,W2)+b2
    z2=sigmoid(a2)
    a3=np.dot(z2,W3)+b3
    y=identity_function(a3)
    return y

network=init_network()
x=np.array([1.0,0.5])
y=forward(network,x)
print(y)

这里定义了 init_network() 和 forward() 函数。 init_network() 函数会进行权重和偏置的初始化，并将它们保存在字典变量 network 中。这个字典变 量 network 中保存了每一层所需的参数（权重和偏置）。 forward() 函数中则封 装了将输入信号转换为输出信号的处理过程。

输出层所用的激活函数，要根据求解问题的性质决定。一般地，回归问题可以使用恒等函数，二元分类问题可以使用 sigmoid函数， 多元分类问题可以使用 softmax函数。

恒等函数和softmax函数

 恒等函数会将输入按原样输出，对于输入的信息，不加以任何改动地直接输出。

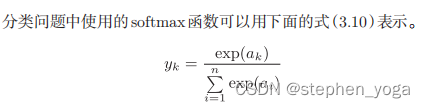
exp( x ) 是表示 e x 的指数函数（ e 是纳皮尔常数 2 . 7182 ... ）。式（ 3 . 10 ）表示假设输出层共有 n 个神经元，计算第 k 个神经元的输出 y k 。如式（ 3 . 10 ）所示， softmax 函数的分子是输入信号 a k 的指数函数，分母是所有输入信号的指数 函数的和。

import numpy as np
a=np.array([0.3,2.9,4.0])
exp_a=np.exp(a)
print(exp_a)
sum_exp_a=np.sum(exp_a)
print(sum_exp_a)
y=exp_a/sum_exp_a
print(y)

#softmax的函数形式
def softmax(a):
    exp_a=np.exp(a)
    sum_exp_a=np.sum(exp_a)
    y=exp_a/sum_exp_a
    return y

实现softmax函数时的注意事项 

softmax存在的问题是会发生溢出导致数据不准确，因此采用下面这种方式进行优化

在进行 softmax 的指数函数的运算时，加上（或者减去）某个常数并不会改变运算的结果。这里的 C ’ 可以使用任何值，但是为了防 止溢出，一般会使用输入信号中的最大值。

def softmax(a):
    c=np.max(a)
    exp_a=np.exp(a-c)
    sum_exp_a=np.sum(exp_a)
    y=exp_a/sum_exp_a
    return y

 softmax函数的特征

 softmax函数的输出是0.0到1.0之间的实数。并且，softmax函数的输出值的总和是1。输出总和为1是softmax函数的一个重要性质。正因为有了这个性质，我们才可以把softmax函数的输出解释为“概率”。