题目:给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

这是一类接口性质的题目;我们只需要在看里面完成这个函数的内容
首先我们来看,他让我们将数组轮转,我们先来分析一下轮转一次的结果,用示例一来演示:

我们先来思考一下就是k如果大于数组的长度呢?我们又是什么情况,假如这里我们的k是10的话是不是和移动3次的结果一样呢,所以这里我们需要去做一个处理,就是:k=k%numsSize,这个就是我们真正要移动的次数;
我们这里有多种解法:
第一种:三段逆置的方法:
第一次就是把前面n-k个数字逆置,
第二次就是将后面k个数字逆置,
第三次就是将我们的整个数组逆置;
所以这里我们只需要先写一个逆置的函数再去调用三次就可以了,这里的时间复杂度是O(N);是一个比较优的解了;

代码:
void ror(int* nums, int leaft, int right)
{
while (leaft < right);
{
int temp = nums[leaft];
nums[leaft] = nums[right];
nums[right] = temp;
leaft++;
right--;
}
}
void rotate(int* nums, int numsSize, int k) {
ror(nums, 0, numsSize - k - 1);
ror(nums, numsSize - k, numsSize - 1);
ror(nums, 0, numsSize - 1);
}
第二种:我们每次就可以把每个后面往前移动,移动k次,我们最开始是用一个变量来存下你要移动的值;在将数组从后往前移动:像这样移动k次;
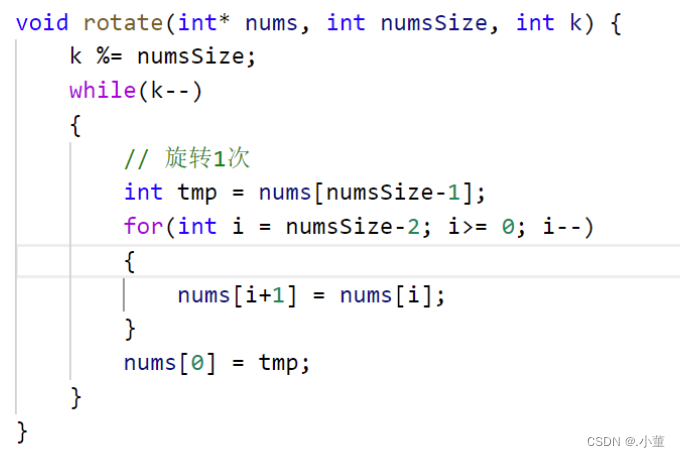
但是这个方法过不了,会超出时间限制;所以看一下这个思路吧,虽然这个解法是一种暴力求解