AES和RSA加解密算法学习笔记(实战版)

news2024/9/28 1:26:18

1. 写在前面

今天整理一篇有关密码学的学习笔记，原因是最近做的一个任务是在网络传输的时候，需要对传输的包进行加密和解密工作，以保证传输过程的安全性。所以，这个过程用到了AES和RSA两个算法。

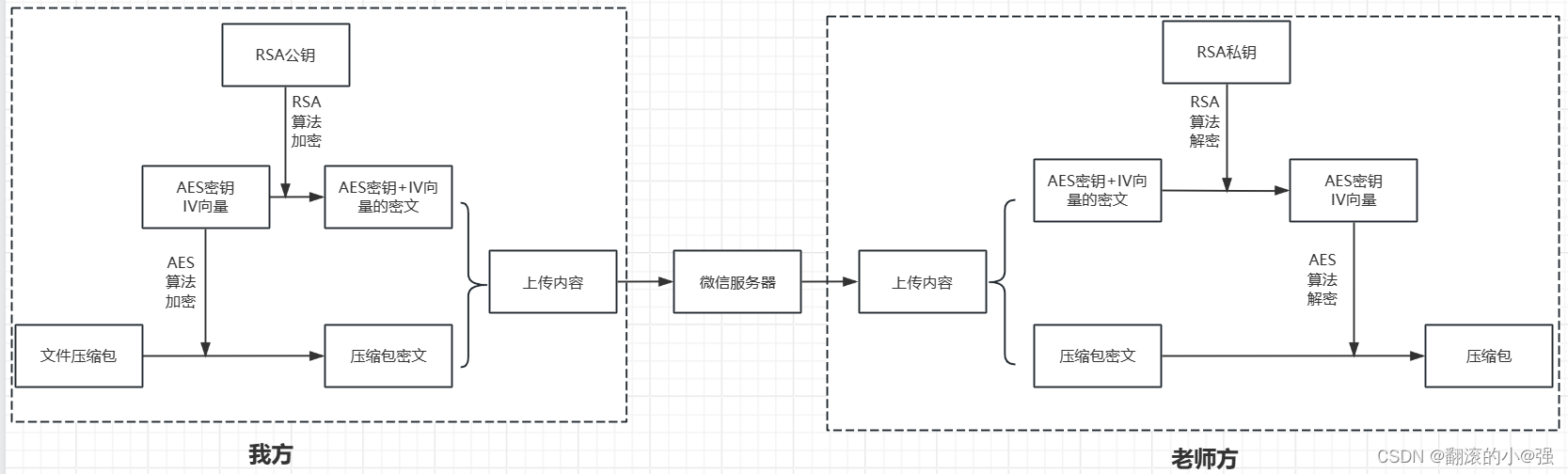
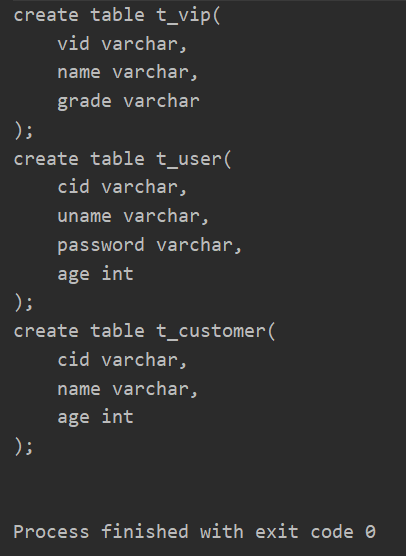
场景：假设我要给我的老师传送毕设代码和论文，我已经把代码和论文打成了一个压缩包，我想把这个压缩包通过微信发过去。但是呢，我担心这个压缩包传递到微信的时候，被人盗取，导致论文和代码泄露，以防万一，我需要对压缩包进行加密传输，到了老师那边，让他解密出来，所以设计了这样的一套流程：

首先，我对压缩包先用AES算法加密，得到压缩包的密文

其次，我把AES算法的密钥，再通过RSA算法加密，得到密钥的密文

我把密钥的密文，压缩包的密文一块写入到密文压缩包，上传到微信，发给老师，然后我把RSA的私钥发短信发给老师

老师拿到密文压缩包，用RSA的私钥，解开压缩包，拿出AES算法的密钥

再用AES算法的密钥解开论文压缩包的密文，就能看代码和论文了

这个过程中，我就不用担心论文和代码泄露了，因为即使微信上有人获取到了压缩包，也无法破解里面的内容，只是一堆乱码而已，保证了传输过程中的安全性。如果用图来看的话，大概是一个这样的逻辑：

这篇文章，主要是想记录下，如何用代码调相关的加密算法，完成上面的加解密流程，关于AES和RSA算法的原理本身，不会涉及太多细节，因为AES算法属实复杂，我其实也没看太懂哈哈，所以只会对这两个算法作简单介绍，知道对称和非对称加密算法，然后知道两个算法的流程，再拿个小例子模拟下流程知道这两个算法在干啥就够了，不用太纠结数学公式的推导啥的。相比这种公式推导，我觉得弄明白上面的流程为啥要这么设计，发送方到底是怎么用这两个算法进行加密的，接收方怎么区分开不同的密文，拿到密钥解密的，这个流程还能应用于什么场景等可能更重要一些。

大纲如下：

AES与RSA算法小识
流程设计
流程实现

ok, let’s go!

2. AES和RSA算法小识

这里简单介绍下两个非常经典的加密算法AES和RSA，首先，先得知道一个事情，就是对称加密和非对称加密，两者的核心区别加密和解密用的秘钥是不是同一个。

对称加密：加密和解密用的密钥是相同的， AES是一种对称加密算法
非对称加密：加密和解密用的密钥不同，一般会有公私钥之分，公钥用来加密，私钥用来解密。RSA是一种非对称加密算法。

2.1 AES算法

AES(Advanced Encryption Standard)，是一种分组加密的对称加密算法。

原理： AES加密，会把明文分成一组一组的，每组长度相等，每次加密一组数据，之道加密整个明文。

AES标准中，分组长度是128位

AES是按照字节加密，每个分组是16个字节

密钥的长度可以使用128， 192和256，密钥长度不同，推荐加密的轮数不同。

整个加密流程大概是下面的样子：
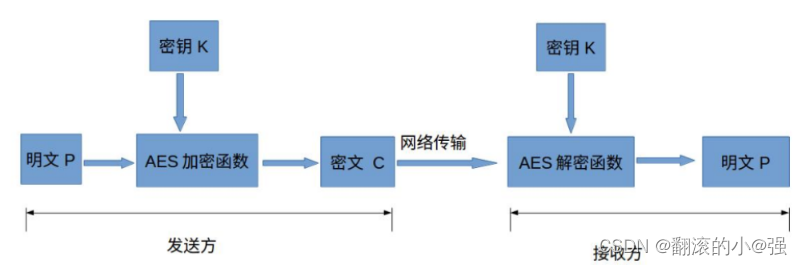
在这里插入图片描述
具体过程比较复杂，我这里不会全介绍，详情可以看参考里面的第一篇链接，我这里大概说下过程。

2.1.1 DES加密算法

在介绍AES加密算法前，先简单介绍下DES加密算法，这是对称密码算法中的分组加密算法。

分组加密是块加密，即把明文划分成固定的字节块，每块加密，然后拼起来。与流密码对应，这个是逐字节进行加密

DES算法的密钥长度64位，其中56位参与运算，其余8位为校验位(8, 16, 25, 32, 40, 48, 56, 64的位置)，示意图如下：
在这里插入图片描述
下面是DES的加密过程：

解密过程比较复杂，感兴趣的话看下面文档吧，这里不整理了。

2.1.2 AES加密算法

为了取代被证明不安全的DES算法而设计，AES算法依然是属于分组加密算法。

明文固定长度为128位，密钥长度128,192,256都可以。
在这里插入图片描述
过程简单描述一下吧，这个更复杂：

解密用相同的密钥去作运算进行解密，这里就不介绍了，可以看下面的第一篇参考文档。

2.2 RSA算法

对称加密算法不好的一点就是两方用的密钥是相同的:

甲方选择某一种加密规则，对信息进行加密；

乙方使用同一种规则，对信息进行解密。

那如何保存和传递密钥是一个比较头疼的问题，1976年，两位美国计算机学家Whitfield Diffie 和 Martin Hellman，提出了一种崭新构思，可以在不直接传递密钥的情况下，完成解密。这被称为"Diffie-Hellman密钥交换算法"。这个算法启发了其他科学家。人们认识到，加密和解密可以使用不同的规则，只要这两种规则之间存在某种对应关系即可，这样就避免了直接传递密钥。

这种新的加密模式被称为"非对称加密算法"。

乙方生成两把密钥（公钥和私钥）。公钥是公开的，任何人都可以获得，私钥则是保密的

甲方获取乙方的公钥，然后用它对信息加密

乙方得到加密后的信息，用私钥解密

如果公钥加密的信息只有私钥解得开，那么只要私钥不泄漏，通信就是安全的。1977年，三位数学家Rivest、Shamir 和 Adleman 设计了一种算法，可以实现非对称加密。这种算法用他们三个人的名字命名，叫做RSA算法。直到现在，RSA算法一直是最广为使用的"非对称加密算法"。

这种算法非常可靠，密钥越长，它就越难破解。根据已经披露的文献，目前被破解的最长RSA密钥是768个二进制位。也就是说，长度超过768位的密钥，还无法破解（至少没人公开宣布）。因此可以认为，1024位的RSA密钥基本安全，2048位的密钥极其安全。

下面简单看下这个算法的原理。

2.2.1 数学知识

在介绍RSA加密算法过程之前，先普及几个数学知识：

互为质数：如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互质关系（coprime）。比如，15和32没有公因子，所以它们是互质关系。这说明，不是质数也可以构成互质关系。
推论：
1. 任意两个质数构成互质关系，比如 $13$ 和 $61$ 。
2. 一个数是质数，另一个数只要不是前者的倍数，两者就构成互质关系，比如 $3$ 和 $10$ 。
3. 如果两个数之中，较大的那个数是质数，则两者构成互质关系，比如 $97$ 和 $57$ 。
4. 1和任意一个自然数是都是互质关系，比如 $1$ 和 $99$ 。
5. p是大于1的整数，则p和p-1构成互质关系，比如 $57$ 和 $56$ 。
6. p是大于1的奇数，则p和p-2构成互质关系，比如 $17$ 和 $15$ 。
欧拉函数：小于 $n$ 的正整数中与 $n$ 互质的数的数目，用 $\phi(n)$ 表示
推论：
1. 如果一个数是质数，则 $\phi(n)=n-1$ (质数只有和1有公约数，所以一个数如果是质数，与比他小的除了1之外的所有数都互质)
2. 如果 $n$ 可以分解成 $2$ 个互质整数之积，则 $\phi(n)=\phi(p) * \phi(q)=(p-1)*(q-1)$
模反元素：如果两个正整数 $e$ 和 $\phi(n)$ 互质，一定可以找到一个整数 $d$ ，使得 $e d - 1$ 被 $\phi(n)$ 整除，此时 $d$ 叫 $e$ 的模反元素。即 $ed-1=k\phi(n),ed \mod \phi(n)=1$