公众号“轻松玩转机器人”，欢迎关注。

1、简介

常用的多项式规划一般泛指3次、5次和7次等多项式规划，4次多项式规划用到的比较少，暂不介绍。

为什么奇数次多项式比较常用呢？因为其有偶数个系数！

偶数个系数有什么用呢？能列偶数个方程来求解，偶数个方程可能包括始末位移、速度和加速度，甚至包括跃度。

一般机器人规划都是点到点的规划，从零速到零速。在某些场景下机器人需要柔顺启停，此时要求启动和停止时的加速度是零，甚至要求始末跃度为零。

下面以5次多项式规划为例进行介绍，其余类型多项式规划类似。

2、原理

5次多项式规划的位移方程：

s = c0 + c1 * t + c2 * t^2 + c3 * t^3 + c4 * t^4 + c5 * t^5

由上式，可以看到5次多项式有6个系数，需要6个方程联立求解，该方程组可以通过以下6个条件得到：

s(0) = 0 %起始位移为零
s(T) = s %终点位移为s
v(0) = 0 %起始速度为零（零速启动）
v(T) = 0 %终点速度为零（零速停止）
a(0) = 0 %起始加速度为零（零加速度启动，柔顺、冲击小）
a(T) = 0 %终点加速度为零（零加速度停止，柔顺、冲击小）

列出上述6个方程就可以解了嘛，答案是不行滴，方程组里还有个未知数T，也就是该运动的时间，一般可以通过如下思路计算：

（1）计算速度最大值（始末时刻及速度导数等于零的时刻），得到位移、运动时间T_v和速度最大值的关系；

（2）计算加速度最大值（始末时刻及加速度导数等于零的时刻），得到位移、运动时间T_a和加速度最大值的关系；

（3）计算跃度最大值（始末时刻及跃度导数等于零的时刻），得到位移、运动时间T_j和跃度最大值的关系。

对于某一款机器人，都有其运动性能参数，如最大速度v_max、最大加速度a_max和最大跃度j_max。分别假设运动过程中达到了最大速度、最大加速度和最大跃度，可以得到三种时间，公式如下：

T_v = 15 * s / (8 * v_max);
T_a = sqrt(10 * s / (sqrt(3) * a_max));
T_j = (60 * s / j_max) ^ (1/3);

运动时间要取三种时间的最大值，否则会存在速度、加速度或跃度超限的问题：

T = max([T_v, T_a, T_j]);

此时再去解方程组，即可得到多项式系数，完成5次多项式规划的创建，更新时只需将时间t代入位移方程即可得到每个时刻的位移。

3、实验

设机器人运动性能：

v_max = 2000;
a_max = 40000;
j_max = 1.8e7;

设运动参数：

s = 25;

位移曲线：

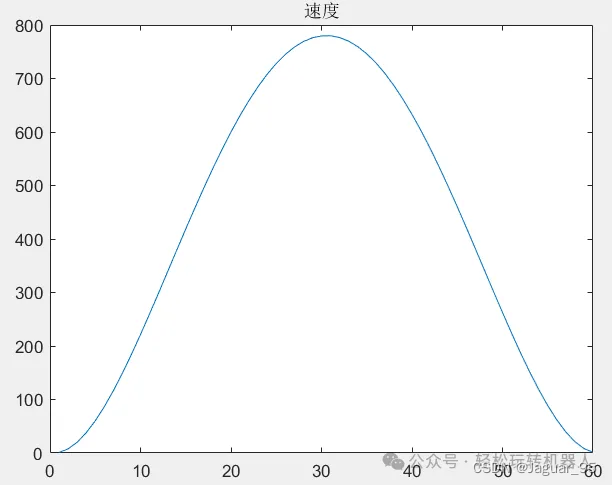
速度曲线：

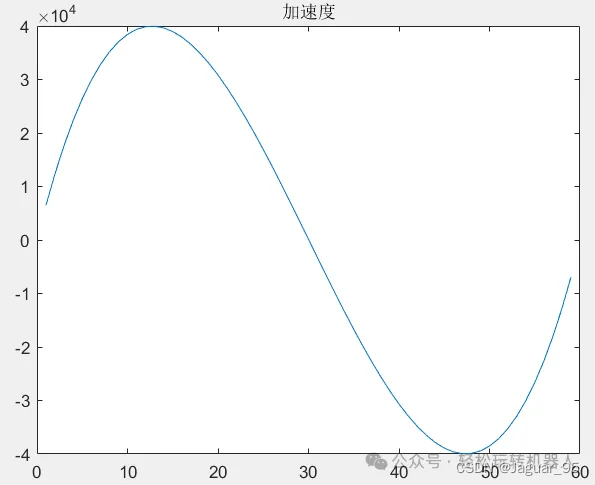
加速度曲线：

跃度曲线：

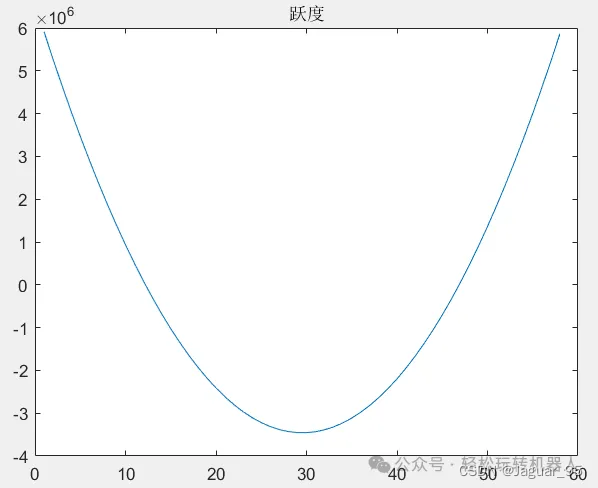
由上述速度、加速度和跃度曲线可以看到：

（1）加速度达到最大值，速度和跃度均没达到最大值，满足计算运动时间的方程和条件；

（2）速度和加速度都是从零开始、以零结束，而跃度则不是，这符合我们求解多项式系数所列的条件。

（3）若要求跃度在运动启动和结束时为零，则要用7次多项式规划，若不要求加速度在启动和结束时为零，则可以降低计算量，用3次多项式规划，原理类似，可以自行求解、测试。