【Yolov系列】Yolov5学习（一）补充1.2：自适应锚框计算详解+代码注释

一、自适应锚框计算详解

自适应锚框计算的具体过程：
①获取数据集中所有目标的宽和高。
②将每张图片中按照等比例缩放的方式到 resize 指定大小，这里保证宽高中的最大值符合指定大小。
③将 bboxes 从相对坐标改成绝对坐标，这里乘以的是缩放后的宽高。
④筛选 bboxes，保留宽高都大于等于两个像素的 bboxes。
⑤使用 k-means 聚类三方得到n个 anchors，与YOLOv3、YOLOv4 操作一样。
⑥使用遗传算法随机对 anchors 的宽高进行变异。倘若变异后的效果好，就将变异后的结果赋值给 anchors；如果变异后效果变差就跳过，默认变异1000次。这里是使用 anchor_fitness 方法计算得到的适应度 fitness，然后再进行评估。

1、k-means聚类算法

k-means是非常经典且有效的聚类方法，通过计算样本之间的距离（相似程度）将较近的样本聚为同一类别（簇）。它属于无监督学习的范畴，与分类不同，聚类不依赖于预先标注的标签，而是尝试将数据集分成由相似对象组成的多个组或“簇”。

术语：

监督学习(supervised learning)：是对具有概念标记（分类）的训练样本进行学习，以尽可能对训练样本集外的数据进行标记（分类）预测。【神经网络和决策树】
无监督学习(unsupervised learning)：是对没有概念标记（分类）的训练样本进行学习，以发现训练样本集中的结构性知识。【聚类】
簇: 所有数据的点集合，簇中的对象是相似的。
质心: 簇中所有点的中心（计算所有点的均值而来）。
SSE: Sum of Sqared Error（误差平方和）, 它被用来评估模型的好坏，SSE 值越小，表示越接近它们的质心. 聚类效果越好。由于对误差取了平方，因此更加注重那些远离中心的点（一般为边界点或离群点）。

优点：

属于无监督学习，无须准备训练集
原理简单，实现起来较为容易
结果可解释性较好

缺点：

需手动设置k值。在算法开始预测之前，我们需要手动设置k值，即估计数据大概的类别个数，不合理的k值会使结果缺乏解释性
可能收敛到局部最小值, 在大规模数据集上收敛较慢
对于异常点、离群点敏感
使用数据类型 : 数值型数据

使用k-means时主要关注两点：

如何表示样本与样本之间的距离（核心问题），这个一般需要根据具体场景去设计，不同的方法聚类效果也不同，最常见的就是欧式距离，在目标检测领域常见的是IOU。
需要分为几类，即k为多少，这个也是需要根据应用场景取选择的超参数。

k-means算法主要流程：

手动设定簇的个数k，假设k=2；
在所有样本中随机选取k个样本作为簇的初始中心，如下图（random clusters）中两个黄色的小星星代表随机初始化的两个簇中心；
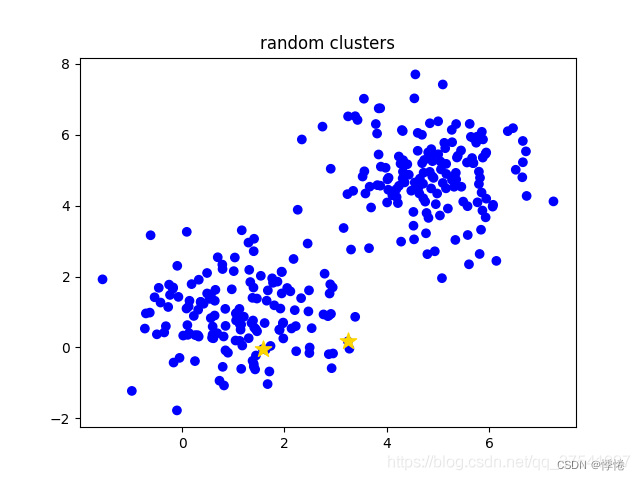
计算每个样本离每个簇中心的距离（这里以欧式距离为例），然后将样本划分到离它最近的簇中。如下图（step 0）用不同的颜色区分不同的簇；
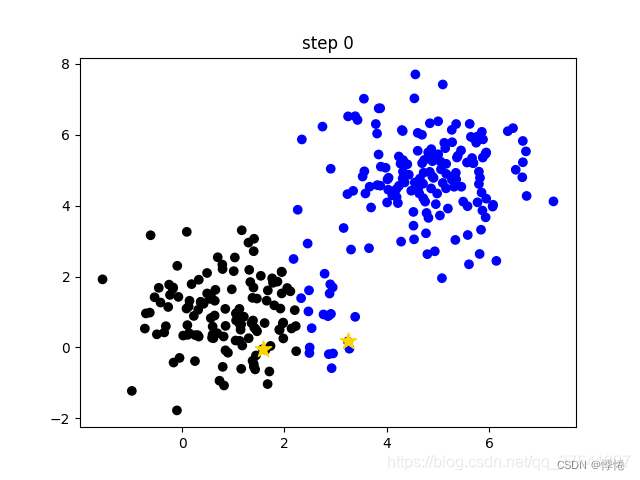
更新簇的中心，计算每个簇中所有样本的均值（方法不唯一）作为新的簇中心。如下图（step 1）所示，两个黄色的小星星已经移动到对应簇的中心；
重复第3步到第4步直到簇中心不在变化或者簇中心变化很小满足给定终止条件。如下图（step2）所示，最终聚类结果。

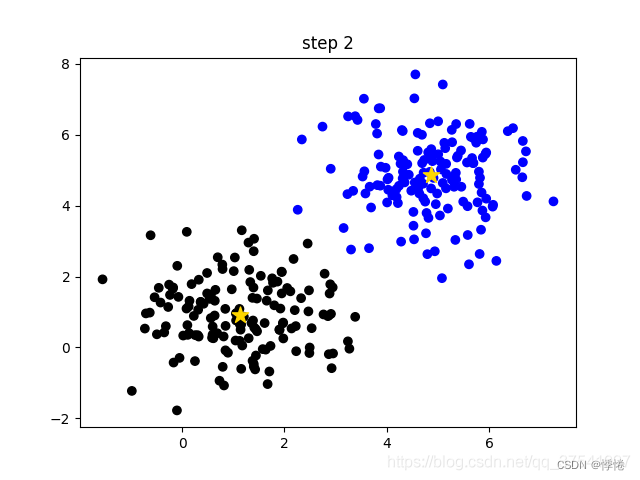
2、bpr(best possible recall)

论文解释：

BPR is defined as the ratio of the number of ground-truth boxes a detector can recall at the most divided by all ground-truth boxes. A ground-truth box is considered being recalled if the box is assigned to at least one sample (i.e., a location in FCOS or an anchor box in anchor-based detectors) during training.

bpr(best possible recall) = 最多能被召回的ground-truth框数量 / 所有ground-truth框数量

bpr最佳召回率最大值为1，越大越好。当最佳召回率大于或等于0.98，则不需要更新锚定框；如果最佳召回率小于0.98，则需要使用k-means聚类算法+遗传进化算法选择出与数据集更匹配的anchors框。

3、白化操作whiten

目的：去除输入数据的冗余信息。假设训练数据是图像，由于图像中相邻像素之间具有很强的相关性，所以用于训练时输入是冗余的；白化的目的就是降低输入的冗余性。

输入数据集X，经过白化处理后，新的数据X’满足两个性质：

特征之间相关性较低；
所有特征具有相同的方差=1

白化的常见的作法：对每一个数据做一个标准差归一化处理（除以标准差）。

scipy.cluster.vq.kmeans() 函数输入的数据就是必须是白化后的数据。相应的输出的anchor k也是白化后的anchor，所以需要将anchor k 都乘以标准差恢复。

4、遗传算法

遗传算法是借鉴生物的自然选择和遗传进化机制面开发出的一种全局优化自适应概率搜索算法。

生物学术语：

遗传（Heredity）：世间的生物从其亲代继承特性或性状的生命现象。

遗传学（Genetics）：研究遗传的科学。
染色体（Chromosome）：细胞中含存的一种微小的丝状化合物，包含生物的所有遗传信息。
基因（Gene）：遗传信息的组成成分，生物的性状是由相应的基因控制的，基因是遗传的单位。
脱氧核糖核酸（Deoxyribonucleiz Acid，简称DNA）：控制并决定生物遗传性状的染色体的组成成分，除此之外，染色体中还含有很多蛋白质。DNA在染色体中有规律地排列着。DNA中，遗传信息在一条长链上按照一定的模式排列，即进行遗传编码。
基因座（Locus）：遗传基因在染色体中所占据的位置。
等位基因（Allele）：同一基因座可能有的全部基因。
复制（Reproduction）：细胞在分裂时，遗传物质DNA复制转移到新产生的细胞，新细胞继承了旧细胞的基因。
交叉（Crossover）：两个同源染色体的某一相同位置处DNA被切断，其前后两串分别交叉组合而形成两个新的染色体。
变异（Mutation）：细胞复制时较小概率产生某些复制差错，从而使DNA发生某种变化，产生新的染色体。，这些新的染色体表现出新的性状。

进化（Evolution）：生命在延续生存的过程中，逐渐适应于其生存环境，使得品质不断得到改良的生命现象。

群体（Population）：生物进化是以集团的形式进行的，这样的团体即为群体。
个体（Individual）：组成群体的单个生物。
适应度（Fitness）：个体对于生存环境的适应能力。

遗传算法中的遗传算子：

选择（Selection）：根据各个个体的适应度，按照一定的规则或者方法，从第t代群体P(t)中选择一些优良的个体遗传给下一代群体P(t+1)中。
交叉（Crossover）：将群体P(t)内的各个个体随机搭配成对，对每一个个体，以某个概率（称为交叉概率，Crossover rate）交换它们之间的染色体。
变异（Mutation）：对群体P(t)中的每一个个体，以某一概率（称为变异概率，Mutation rate）改变某一个或某一些基因座上的基因值为其他的等位基因。

遗传算法运算过程示意图：

初始化。设置进化代数计算器t=0；设置最大进化代数T；随机生成M个个体作为初始群体P(0)。
个体评价。计算群体P(t)中各个个体的适应度。
选择运算。将选择算子作用于群体。
交叉运行。将交叉运算作用于群体。
变异运算。将变异运算作用于群体。群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1)。
终止判断条件。若t<=T，则t=t+1，转到2；若t>T，则以进化过程中所得到的具有最大适应度的个体作为最优解输出，终止计算。

遗传算法手工模拟计算：

f(x1,x2)为目标函数，x1，x2为两个自变量，下方为自变量的取值范围。

运算过程：

个体编码。遗传算法的运算对象是表示个体的符号串，所以必须把变量x1、x2编码为一种符号串。x1、x2的取值范围均为0~7之间的整数，可分别用3位无符号二进制整数来表示，将它们连接一起所组成的6位无符号二进制整数就形成了个体的基因型，表示一个可行解。例如，基因型X=101110所对应的表现型是X=[5,6]T。个体的表现型x和基因型X之间可通过编码和解码程序相互转换。（编码形式不固定，此处采用的无符号二进制整数编码）
初始群体的产生。遗传算法是对群体进行的进化操作，需要给其准备一些表示起始搜索点的初始群体数据。本例中，群体规模的大小取为4，即群体由4个个体组成，每个个体可通过随机方法产生。
适应度计算。遗传算法中以个体的适应度大小来评定各个个体的优劣程度，从而决定其遗传机会的大小。本例中，目标函数总取非负值，并且是以求函数最大值为优化目标，故可直接
利用目标函数值作为个体的适应度。为计算函数的目标值，需先对个体基因型X进行解码。（不同案例中适应度函数选取不同）

遗传算法手工模拟计算图示：

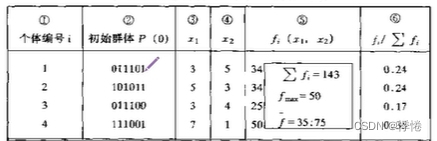
（1）初始群体P(0)产生
第一列为初始群体中个体的编号；第二列为选取的初始群体中的个体基因型X；三、四列为基因型所对应的表现型，基因型中前三位对应x1，后三位对应x2；第五列为适应度计算，以目标函数为适应度函数；第六列为每个个体适应度所占的比例。

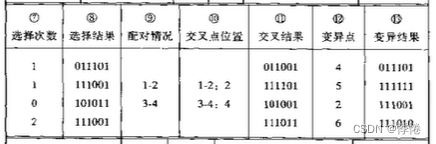
（2）选择算子运算
选择次数为对初始群体中个体适应度进行比较，三号个体适应度最低不进行下一步计算，选择次数为0，4号个体适应度最高，复制两次进入下一步计算，1、2号个体分别复制一次进入下一步计算，保证下一步计算群体规模不变。
选择结果列中二、四行均为初始4号个体，一、三行为初始1、2号个体。
（3）交叉算子运算
配对情况列中前两个个体进行配对，后两个个体进行配对。
交叉点位置随机选取（基因型X中从左至右，第一位为1号位置），前两个配对个体选择3号位置，3号位置之后的基因段（101和001）进行等位基因交换，后两个配对个体选择4号位置，4号位置之后的基因段（11和01）进行等位基因交换。
（4）变异算子运算
随机选取基因型X中点位置进行突变，0<->1。

（4）子代群体P(1)产生
观察表现型变化，重复进行上述计算。
（5）输出最优解
迭代上述过程直至满足迭代次数，终止迭代，输出最优解。

二、自适应锚框计算代码详解

ps：注释中的尺寸及计算数值均基于自己本地数据集，不同数据集所对应的值有所不同。

0、导入包

import random                   # 随机生成模块

import numpy as np              # numpy矩阵操作模块
import torch                    # Pytorch深度学习模块
import yaml                     # 操作yaml文件模块
from tqdm import tqdm           # Python进度条模块

from utils import TryExcept
from utils.general import LOGGER, TQDM_BAR_FORMAT, colorstr

PREFIX = colorstr("AutoAnchor: ")    # 一些可视化: AutoAnchor: Analyzing anchors...

1、check_anchor_order函数

这个函数用于确认当前anchors和stride的顺序是否是一致的，因为我们的m.anchors是相对各个feature map（每个feature map的感受野不同检测的目标大小也不同适合的anchor大小也不同）所以必须要顺序一致否则效果会很不好。这个函数一般用于check_anchors最后阶段。

def check_anchor_order(m):
    """
    用在check_anchors最后 确定anchors和stride的顺序是一致的
    Checks and corrects anchor order against stride in YOLOv5 Detect() module if necessary.
    :params m: model中的最后一层 Detect层
    """
    # 计算每个输出层anchor的平均面积 anchor area
    # tensor([  456.33334,  3880.33325, 54308.66797])
    a = m.anchors.prod(-1).mean(-1).view(-1)  # mean anchor area per output layer
    # 计算最大均值anchor和最小均值anchor的面积差
    # tensor(53852.33594)
    da = a[-1] - a[0]  # delta a
    # 计算最大stride与最小stride差
    # tensor(24.)
    ds = m.stride[-1] - m.stride[0]  # delta s
    # torch.sign(x):当x大于/小于0时，返回1/-1
    # 如果这里anchor与stride顺序不一致，则重新调整顺序
    if da and (da.sign() != ds.sign()):  # same order
        LOGGER.info(f"{PREFIX}Reversing anchor order")
        m.anchors[:] = m.anchors.flip(0)

2、check_anchors函数

这个函数是通过计算bpr确定是否需要改变anchors 需要就调用k-means重新计算anchors。

@TryExcept(f"{PREFIX}ERROR")
def check_anchors(dataset, model, thr=4.0, imgsz=640):
    """
    用于train.py中,通过bpr确定是否需要改变anchors,需要就调用k-means重新计算anchors
    Evaluates anchor fit to dataset and adjusts if necessary, supporting customizable threshold and image size.
    :params dataset: 自定义数据集LoadImagesAndLabels返回的数据集
    :params model: 初始化的模型
    :params thr: 超参中得到  界定anchor与label匹配程度的阈值
    :params imgsz: 图片尺寸 默认640
   """
    # m: 从model中取出最后一层(Detect)
    m = model.module.model[-1] if hasattr(model, "module") else model.model[-1]  # Detect()
    # dataset.shapes.max(1, keepdims=True) = 每张图片的较长边
    # shapes: 将数据集图片的最长边缩放到img_size, 较小边相应缩放,得到新的所有数据集图片的宽高 [N, 2]  N训练集图片数量
    # imgaz:320, train训练集中有107张1366*768训练图, dataset.shapes:[[1366  768] ... [1366  768]], dataset.shapes.max(1, keepdims=True):[1366 ... 1366]
    # shapes:[[320, 179.91] ... [320, 179.91]]
    shapes = imgsz * dataset.shapes / dataset.shapes.max(1, keepdims=True)
    # 产生随机数scale (107, 1)
    scale = np.random.uniform(0.9, 1.1, size=(shapes.shape[0], 1))  # augment scale
    # torch.Size([855, 2])  所有target(855个)基于原图大小的wh     shapes * scale: 随机化尺度变化
    wh = torch.tensor(np.concatenate([l[:, 3:5] * s for s, l in zip(shapes * scale, dataset.labels)])).float()  # wh
    # tensor([[15.48895, 15.88619],
    #         [16.28319, 20.65190],
    #         [20.25471, 14.29750],
    #         ...,
    #         [15.86208, 10.57459],
    #         [15.38139, 13.93932],
    #         [18.26520, 19.22661]])
    def metric(k):
        """用在check_anchors函数中  compute metric
        根据数据集的所有图片的wh和当前所有anchors k计算 bpr(best possible recall) 和 aat(anchors above threshold)
        :params k: anchors [9, 2]  wh: [N, 2]
        :return bpr: best possible recall 最多能被召回(通过thr)的gt框数量 / 所有gt框数量   小于0.98 才会用k-means计算anchor
        :return aat: anchors above threshold 每个target平均有多少个anchors
        """
        # None添加维度  所有target(gt)的wh wh[:, None] [855, 2]->[855, 1, 2]
        #             所有anchor的wh k[None] [9, 2]->[1, 9, 2]
        # r: target的高h宽w与anchor的高h_a宽w_a的比值，即h/h_a, w/w_a  [855, 9, 2]  有可能大于1，也可能小于等于1
        r = wh[:, None] / k[None]
        # x 高宽比和宽高比的最小值 无论r大于1，还是小于等于1最后统一结果都要小于1   [855, 9]
        x = torch.min(r, 1 / r).min(2)[0]  # ratio metric
        # best [855] 为每个gt框选择匹配所有anchors宽高比例值最好的那一个比值
        best = x.max(1)[0]  # best_x
        # aat(anchors above threshold)  [1]     每个target平均有多少个anchors
        # sum(axis), # 当axis=1时，求的是每一行元素的和
        aat = (x > 1 / thr).float().sum(1).mean()  # anchors above threshold
        # bpr(best possible recall) = 最多能被召回(通过thr)的gt框数量 / 所有gt框数量   小于0.98 才会用k-means计算anchor
        # 所有标签与anchors宽高比例列表x中取每行最大的比值得到best列表，best中大于1/阈值的比值的平均值
        bpr = (best > 1 / thr).float().mean()  # best possible recall
        return bpr, aat

    # stride:tensor([[[ 8.]],
    # 
    #               [[16.]],
    # 
    #               [[32.]]])
    stride = m.stride.to(m.anchors.device).view(-1, 1, 1)  # model strides

    # print(m.anchors)
    # tensor([[[ 1.25000,  1.62500],
    #          [ 2.00000,  3.75000],
    #          [ 4.12500,  2.87500]],
    # 
    #         [[ 1.87500,  3.81250],
    #          [ 3.87500,  2.81250],
    #          [ 3.68750,  7.43750]],
    # 
    #         [[ 3.62500,  2.81250],
    #          [ 4.87500,  6.18750],
    #          [11.65625, 10.18750]]])
    # anchors: [N,2]  所有anchors的宽高   基于缩放后的图片大小(较长边为640 较小边相应缩放)
    anchors = m.anchors.clone() * stride  # current anchors
    # print(anchors)
    # tensor([[[ 10.,  13.],
    #          [ 16.,  30.],
    #          [ 33.,  23.]],
    # 
    #         [[ 30.,  61.],
    #          [ 62.,  45.],
    #          [ 59., 119.]],
    # 
    #         [[116.,  90.],
    #          [156., 198.],
    #          [373., 326.]]])
    
    # 计算出数据集所有图片的wh和当前所有anchors的bpr和aat
    # bpr: bpr(best possible recall): 最多能被召回(通过thr)的gt框数量 / 所有gt框数量  [1] 0.96223  小于0.98 才会用k-means计算anchor
    # aat(anchors past thr): [1] 3.54360 通过阈值的anchor个数
    bpr, aat = metric(anchors.cpu().view(-1, 2))
    s = f"\n{PREFIX}{aat:.2f} anchors/target, {bpr:.3f} Best Possible Recall (BPR). "
    # threshold to recompute
    # 考虑这9类anchor的宽高和gt框的宽高之间的差距, 如果bpr<0.98(说明当前anchor不能很好的匹配数据集gt框)就会根据k-means算法重新聚类新的anchor
    if bpr > 0.98:  # threshold to recompute
        LOGGER.info(f"{s}Current anchors are a good fit to dataset ✅")
    else:
        LOGGER.info(f"{s}Anchors are a poor fit to dataset ⚠️, attempting to improve...")
        na = m.anchors.numel() // 2  # number of anchors
        # 如果bpr<0.98(最大为1 越大越好) 使用k-means + 遗传进化算法选择出与数据集更匹配的anchors框  [9, 2]
        anchors = kmean_anchors(dataset, n=na, img_size=imgsz, thr=thr, gen=1000, verbose=False)
        # 计算新的anchors的new_bpr
        new_bpr = metric(anchors)[0]
        # 比较k-means + 遗传进化算法进化后的anchors的new_bpr和原始anchors的bpr
        # 注意: 这里并不一定进化后的bpr必大于原始anchors的bpr, 因为两者的衡量标注是不一样的  进化算法的衡量标准是适应度 而这里比的是bpr
        if new_bpr > bpr:  # replace anchors
            anchors = torch.tensor(anchors, device=m.anchors.device).type_as(m.anchors)
            # 替换m的anchors
            m.anchors[:] = anchors.clone().view_as(m.anchors)
            # 检查anchor顺序和stride顺序是否一致 不一致就调整
            # 因为我们的m.anchors是相对各个feature map 所以必须要顺序一致 否则效果会很不好
            check_anchor_order(m)  # must be in pixel-space (not grid-space)
            # 替换m的anchors(相对各个feature map)      [9, 2] -> [3, 3, 2]
            m.anchors /= stride
            s = f"{PREFIX}Done ✅ (optional: update model *.yaml to use these anchors in the future)"
        else:
            s = f"{PREFIX}Done ⚠️ (original anchors better than new anchors, proceeding with original anchors)"
        LOGGER.info(s)

此函数在train.py中调用：

from utils.autoanchor import check_anchors


# check_anchors函数，计算默认锚框anchor与数据集标签框的高宽比
# 标签的高h宽w与anchor的高h_a宽h_b的比值 即h/h_a，w/w_a都要在(1/hyp['anchor_t']，hyp['anchor_t'])是可以接受的#如果bpr小于98%，则根据k-mean算法聚类新的锚框
if not resume:
    if not opt.noautoanchor:
    check_anchors(dataset, model=model, thr=hyp["anchor_t"], imgsz=imgsz)  # run AutoAnchor
    model.half().float()  # pre-reduce anchor precision

3、kmean_anchors函数

这个函数是这个这个文件的核心函数，功能：使用k-means算法 + 遗传算法，算出更符合当前数据集的anchors。

这里不仅仅使用了k-means聚类，还使用了Genetic Algorithm遗传算法，在k-means聚类的结果上进行变异（mutation）。接下来简单介绍下代码流程：

载入数据集，得到数据集中所有数据的宽w和高h；
将每张图片中宽w和高h的最大值等比例缩放到指定大小imgsz，较小边也相应缩放；
将标签框（bboxes）从相对坐标改成绝对坐标（乘以缩放后的wh）；
筛选标签框（bboxes），保留wh都大于等于两个像素的标签框（bboxes）；
使用k-means聚类得到n个anchors（调用k-means包，涉及一个白化操作）
使用遗传算法随机对anchors的wh进行变异，如果变异后效果变得更好（使用anchor_fitness方法计算得到的fitness（适应度）进行评估）就将变异后的结果赋值给anchors，如果变异后效果变差就跳过，默认变异1000次

遗传算法可以查看前面遗传算法介绍，或者可以观看b站视频：【遗传算法超细致+透彻理解】

def kmean_anchors(dataset="./data/coco128.yaml", n=9, img_size=640, thr=4.0, gen=1000, verbose=True):
    """
    Creates kmeans-evolved anchors from training dataset.
    调用K-means算法+遗传算法算出更符合当前数据集的anchors
    Arguments:
        dataset: path to data.yaml, or a loaded dataset     数据集的路径/数据集本身
        n: number of anchors        anchor框的个数
        img_size: image size used for training      数据集图片的大小
        thr: anchor-label wh ratio threshold hyperparameter hyp['anchor_t'] used for training, default=4.0      阈值 由hyp['anchor_t']参数控制
        gen: generations to evolve anchors using genetic algorithm      遗传算法进化迭代的次数(突变 + 选择)
        verbose: print all results      是否打印所有的进化(成功的)结果 默认传入是Fasle的 只打印最佳的进化结果即可

    Return:
        k: kmeans evolved anchors       k-means算法 + 遗传算法进化后的anchors

    Usage:
        from utils.autoanchor import *; _ = kmean_anchors()
    """
    from scipy.cluster.vq import kmeans

    npr = np.random
    # 下面的thr不是传入的thr，而是1/thr, 在计算指标这方面还是和check_anchor一样
    thr = 1 / thr

    def metric(k, wh):  # compute metrics
        """用于print_results函数和anchor_fitness函数
            计算ratio metric: 整个数据集的gt框与anchor对应宽比和高比即:gt_w/k_w,gt_h/k_h + x + best_x  用于后续计算bpr+aat
            注意我们这里选择的metric是gt框与anchor对应宽比和高比 而不是常用的iou 这点也与nms的筛选条件对应 是yolov5中使用的新方法
            :params k: anchor框
            :params wh: 整个数据集的wh [N, 2]
            :return x: [N, 9] N个gt框与所有anchor框的宽比或高比(两者之中较小者)
            :return x.max(1)[0]: [N] N个gt框与所有anchor框中的最大宽比或高比(两者之中较小者)
        """
        # [N, 1, 2] / [1, 9, 2] = [N, 9, 2]  N个gt_wh和9个anchor的k_wh宽比和高比
        # 两者的重合程度越高 就越趋近于1 远离1(<1 或 >1)重合程度都越低
        r = wh[:, None] / k[None]
        # r=gt_height/anchor_height  gt_width / anchor_width  有可能大于1，也可能小于等于1
        # torch.min(r, 1. / r): [N, 9, 2] 将所有的宽比和高比统一到<=1
        # .min(2): value=[N, 9] 选出每个gt个和anchor的宽比和高比最小的值   index: [N, 9] 这个最小值是宽比(0)还是高比(1)
        # [0] 返回value [N, 9] 每个gt个和anchor的宽比和高比最小的值, 就是所有gt与anchor重合程度最低的
        x = torch.min(r, 1 / r).min(2)[0]  # ratio metric
        # x = wh_iou(wh, torch.tensor(k))  # iou metric
        # x.max(1)[0]: [N] 返回每个gt和所有anchor(9个)中宽比或高比最大的值
        return x, x.max(1)[0]  # x, best_x

    def anchor_fitness(k):  # mutation fitness
        """用于kmean_anchors函数
            适应度计算 优胜劣汰 用于遗传算法中衡量突变是否有效的标注 如果有效就进行选择操作 没效就继续下一轮的突变
            :params k: [9, 2] k-means生成的9个anchors     wh: [N, 2]: 数据集的所有gt框的宽高
            :return (best * (best > thr).float()).mean()=适应度计算公式 [1] 注意和bpr有区别 这里是自定义的一种适应度公式
                    返回的是输入此时anchor k 对应的适应度
        """
        _, best = metric(torch.tensor(k, dtype=torch.float32), wh)
        return (best * (best > thr).float()).mean()  # fitness

    def print_results(k, verbose=True):
        """用于kmean_anchors函数中打印k-means计算相关信息
            计算bpr、aat=>打印信息: 阈值+bpr+aat  anchor个数+图片大小+metric_all+best_mean+past_mean+Kmeans聚类出来的anchor框(四舍五入)
            :params k: k-means得到的anchor k
            :return k: input
        """
        # 将k-means得到的anchor k按面积从小到大啊排序
        k = k[np.argsort(k.prod(1))]  # sort small to large
        # x: [N, 9] N个gt框与所有anchor框的宽比或高比(两者之中较小者)
        # best: [N] N个gt框与所有anchor框中的最大宽比或高比(两者之中较小者)
        x, best = metric(k, wh0)
        # (best > thr).float(): True=>1.  False->0.  .mean(): 求均值
        # bpr(best possible recall): 最多能被召回(通过thr)的gt框数量 / 所有gt框数量  [1]  小于0.98 才会用k-means计算anchor
        # aat(anchors above threshold): [1] 每个target平均有多少个anchors
        bpr, aat = (best > thr).float().mean(), (x > thr).float().mean() * n  # best possible recall, anch > thr
        s = (
            f"{PREFIX}thr={thr:.2f}: {bpr:.4f} best possible recall, {aat:.2f} anchors past thr\n"
            f"{PREFIX}n={n}, img_size={img_size}, metric_all={x.mean():.3f}/{best.mean():.3f}-mean/best, "
            f"past_thr={x[x > thr].mean():.3f}-mean: "
        )
        for x in k:
            s += "%i,%i, " % (round(x[0]), round(x[1]))
        if verbose:
            LOGGER.info(s[:-2])
        return k

    # 载入数据集
    if isinstance(dataset, str):  # *.yaml file
        with open(dataset, errors="ignore") as f:
            data_dict = yaml.safe_load(f)  # model dict
        from utils.dataloaders import LoadImagesAndLabels

        dataset = LoadImagesAndLabels(data_dict["train"], augment=True, rect=True)

    # Get label wh
    # 得到数据集中所有数据的wh
    # 将数据集图片的最长边缩放到img_size, 较小边相应缩放
    shapes = img_size * dataset.shapes / dataset.shapes.max(1, keepdims=True)
    # 将原本数据集中gt boxes归一化的wh缩放到shapes尺度
    wh0 = np.concatenate([l[:, 3:5] * s for s, l in zip(shapes, dataset.labels)])  # wh

    # Filter
    # 统计gt boxes中宽或者高小于3个像素的个数, 目标太小, 发出警告
    i = (wh0 < 3.0).any(1).sum()
    if i:
        LOGGER.info(f"{PREFIX}WARNING ⚠️ Extremely small objects found: {i} of {len(wh0)} labels are <3 pixels in size")
    # 筛选出label大于2个像素的框拿来聚类,[...]内的相当于一个筛选器,为True的留下
    wh = wh0[(wh0 >= 2.0).any(1)].astype(np.float32)  # filter > 2 pixels
    # wh = wh * (npr.rand(wh.shape[0], 1) * 0.9 + 0.1)  # multiply by random scale 0-1

    # Kmeans init
    try:
        # Kmeans聚类方法: 使用欧式距离来进行聚类
        LOGGER.info(f"{PREFIX}Running kmeans for {n} anchors on {len(wh)} points...")
        assert n <= len(wh)  # apply overdetermined constraint
        # 计算宽和高的标准差->[w_std,h_std]
        s = wh.std(0)  # sigmas for whitening
        # 开始聚类,仍然是聚成n类,返回聚类后的anchors k(这个anchor k是白化后数据的anchor框)
        # 另外还要注意的是这里的kmeans使用欧式距离来计算的
        # 运行k-means的次数为30次  obs: 传入的数据必须先白化处理 'whiten operation'
        # 白化处理: 新数据的标准差=1 降低数据之间的相关度，不同数据所蕴含的信息之间的重复性就会降低，网络的训练效率就会提高
        # 白化操作博客: https://blog.csdn.net/weixin_37872766/article/details/102957235
        # k*s 得到原来数据(白化前)的anchor框
        k = kmeans(wh / s, n, iter=30)[0] * s  # points
        assert n == len(k)  # kmeans may return fewer points than requested if wh is insufficient or too similar
    except Exception:
        LOGGER.warning(f"{PREFIX}WARNING ⚠️ switching strategies from kmeans to random init")
        k = np.sort(npr.rand(n * 2)).reshape(n, 2) * img_size  # random init
    wh, wh0 = (torch.tensor(x, dtype=torch.float32) for x in (wh, wh0))
    # 输出新算的anchors k 相关的信息
    k = print_results(k, verbose=False)

    # Plot
    # k, d = [None] * 20, [None] * 20
    # for i in tqdm(range(1, 21)):
    #     k[i-1], d[i-1] = kmeans(wh / s, i)  # points, mean distance
    # fig, ax = plt.subplots(1, 2, figsize=(14, 7), tight_layout=True)
    # ax = ax.ravel()
    # ax[0].plot(np.arange(1, 21), np.array(d) ** 2, marker='.')
    # fig, ax = plt.subplots(1, 2, figsize=(14, 7))  # plot wh
    # ax[0].hist(wh[wh[:, 0]<100, 0],400)
    # ax[1].hist(wh[wh[:, 1]<100, 1],400)
    # fig.savefig('wh.png', dpi=200)

    # Evolve    类似遗传/进化算法  变异操作
    # f: fitness 
    # sh: (9,2)
    # mp: 突变比例mutation prob=0.9   s: sigma=0.1
    f, sh, mp, s = anchor_fitness(k), k.shape, 0.9, 0.1  # fitness, generations, mutation prob, sigma
    pbar = tqdm(range(gen), bar_format=TQDM_BAR_FORMAT)  # progress bar
    # 根据聚类出来的n个点采用遗传算法生成新的anchor
    for _ in pbar:
        # 重复1000次突变+选择 选择出1000次突变里的最佳anchor k和最佳适应度f
        v = np.ones(sh) # v [9, 2] 全是1
        while (v == 1).all():  # 产生变异规则 mutate until a change occurs (prevent duplicates)
            # npr.random(sh) < mp: 让v以90%的比例进行变异  选到变异的就为1  没有选到变异的就为0
            v = ((npr.random(sh) < mp) * random.random() * npr.randn(*sh) * s + 1).clip(0.3, 3.0)
        # 变异(改变这一时刻之前的最佳适应度对应的anchor k)
        kg = (k.copy() * v).clip(min=2.0)
        # 计算变异后的anchor kg的适应度
        fg = anchor_fitness(kg)
        # 如果变异后的anchor kg的适应度>最佳适应度k 就进行选择操作
        if fg > f:
            # 选择变异后的anchor kg为最佳的anchor k 变异后的适应度fg为最佳适应度f
            f, k = fg, kg.copy()
            pbar.desc = f"{PREFIX}Evolving anchors with Genetic Algorithm: fitness = {f:.4f}"
            if verbose:
                print_results(k, verbose)

    return print_results(k).astype(np.float32)

原始anchor bpr>0.98就不会更新anchors：