基于Iris flower数据集的kNN分类实战
Iris data set(鸢尾花数据集简介)
鸢尾花数据集共包含三种鸢尾花:Iris setosa, Iris virginica and Iris versicolor。



(图片来源见参考文献【2】【3】【4】)
Iris deta set共有150x4个数据。每种花有50组描述feature的子数据集,每个feature的子集包含四个feature,他们是,sepal length花瓣的长度,sepal width花瓣的宽度,petal length花萼的长度和petal width花萼的宽度(单位都是cm)。


(图片来源见参考文献【8】【10】)
Iris中的前50组数据是山鸢尾,这是部分数据:
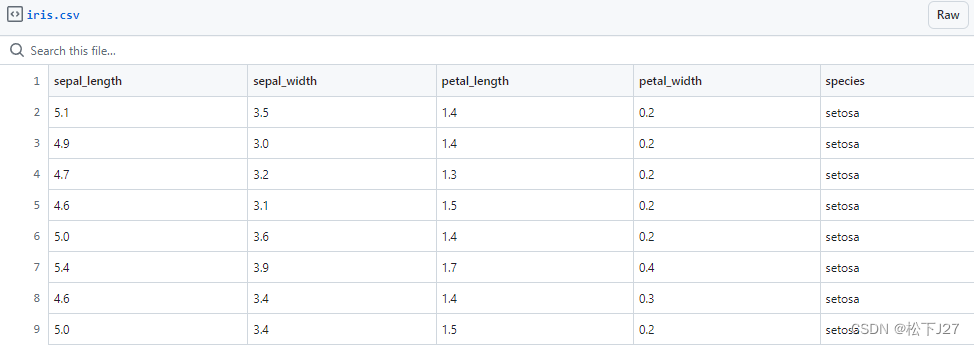
Iris中的51~100组数据是变色鸢尾,这是部分数据:
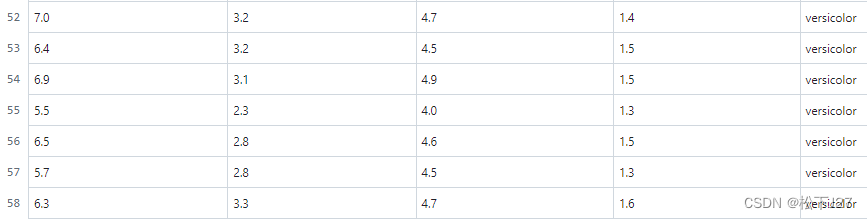
Iris中的101~150组数据是维吉尼亚鸢尾,这是部分数据:
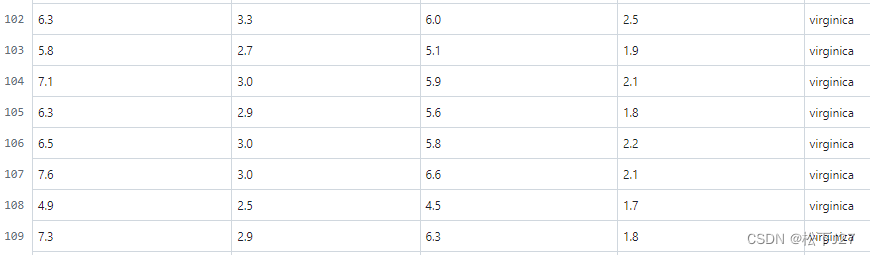
单从花萼的数据上看(也就是数据中的后两列),我发现维吉尼亚鸢尾花和变色鸢尾花的花萼要比山鸢尾的花萼大的多(尽管这一点在我给出的图片上看的不是很明显),而且,维吉尼亚鸢尾花的花萼也比变色鸢尾花的略大一些。
但如果只看花瓣的话(数据中的前两列),维吉尼亚鸢尾花与变色鸢尾花的尺寸相差无几。只山鸢尾的花瓣会显得比较短。
训练数据集
现在我们的问题是,如果你在马路边看到了一束鸢尾花,怎么根据现有的数据集去判断她属于哪一种鸢尾花?这篇文章就是我自己在网上学习用kNN算法安装我们输入的参数去训练数据集,然后,基于这个训练好的数据集去判断我们在马路边看到的花属于三者中的哪一类。
整个过程的整体思路大致是这样的:
1,导入整个数据集并在数据集中选择你需要的数据
2,查考数据的大致分布情况
3,构建一个kNN分类器
4,用构建好的kNN分类器对我们感兴趣的数据进行分类
5,把新的数据丢到训练好的分类器中进行分类
Python实战(平台Vs code)
1,导入训练过程中要用到的所有python软件包
语法:import + 模块名
import + 模块名= 导入整个模块
#kNN leanring iris classify @CSDN_J27,2024/04/19
import numpy as np #将NumPy库导入到Python程序中,并使用别名“np”来表示该库。
import matplotlib.pyplot as plt2,导入Iris数据集,选择你要用到的数据
语法:from 模块名 import 对象1, 对象2, ...
from + import 用于导入某个模块中的指定对象(如函数、类等)
from sklearn import datasets #导入sklearn中的数据集datasets
iris = datasets.load_iris() #导入iris的数据库
x_train_sepal = iris.data[:, 0:2] #取特征数据中的后两列
x_train_petal = iris.data[:, 2:4] #取特征数据中的后两列
y_train = iris.target#种类标签,一个数据对应一类iris,一类iris对应一组sepal的长宽和一组petal的长宽,这四个feature。
在上面的操作中,我先是导入了datasets,然后把datasets中的iris数据集赋给了iris。然后,我把iris分成两部分,分别赋给了x_train_sepal和x_train_petal,他们分别保存iris中的花瓣数据和花萼数据,又因为类别标签是共用的所以,只需把储存类别的数据赋给y_train即可。
3,绘制花瓣和花萼数据的散点图
#绘制三组花瓣样本的散点图
color1 = ("black", "blue", "green")
fig1,ax_sepal=plt.subplots()
ax_sepal.scatter(x_train_sepal[:50, 0], x_train_sepal[:50, 1], c = color1[0], marker='o', label='setosa')
ax_sepal.scatter(x_train_sepal[50:100, 0], x_train_sepal[50:100, 1], c = color1[1], marker='o', label='versicolor')
ax_sepal.scatter(x_train_sepal[100:, 0], x_train_sepal[100:, 1], c = color1[2], marker='o', label='Virginica')
ax_sepal.legend(loc=2)
ax_sepal.set_xlabel('sepal length(cm)')
ax_sepal.set_ylabel('sepal width(cm)')
plt.show(block=False)
fig2,ax_petal=plt.subplots()
color2 = ("navy", "maroon", "teal")
ax_petal.scatter(x_train_petal[:50, 0], x_train_petal[:50, 1], c = color2[0], marker='^', label='setosa')
ax_petal.scatter(x_train_petal[50:100, 0], x_train_petal[50:100, 1], c = color2[1], marker='^', label='versicolor')
ax_petal.scatter(x_train_petal[100:, 0], x_train_petal[100:, 1], c = color2[2], marker='^', label='Virginica')
ax_petal.legend(loc=2)
ax_petal.set_xlabel('petal length(cm)')
ax_petal.set_ylabel('petal width(cm)')
plt.show(block=False)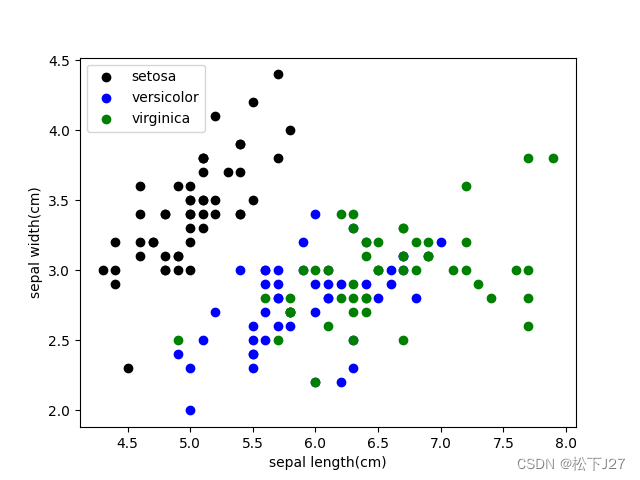
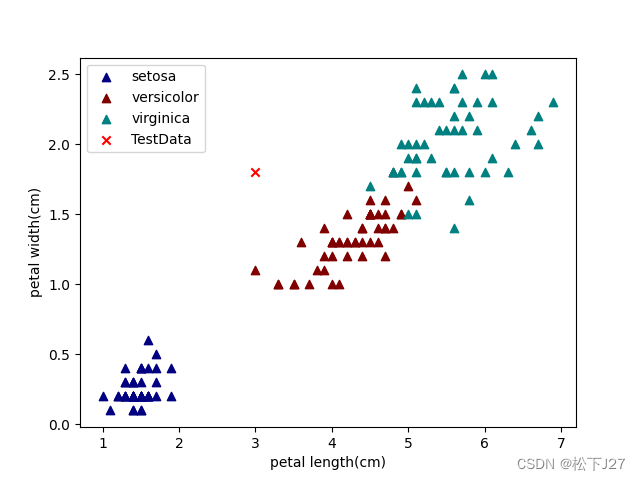
花瓣feature的散点图
这和我在上面从数据上看给出的分析一样, virginica维吉尼亚鸢尾花与versicolor变色鸢尾花的尺寸相差无几,因此在已有的数据库中他们二者的分布基本上都混合到一起了。而setosa山鸢尾的花瓣比另外两个都要短一些。这就是说,如果单单基于花瓣的尺寸去对新数据进行分类的话,只能把setosa与virginica+versicolor这两大类分开。
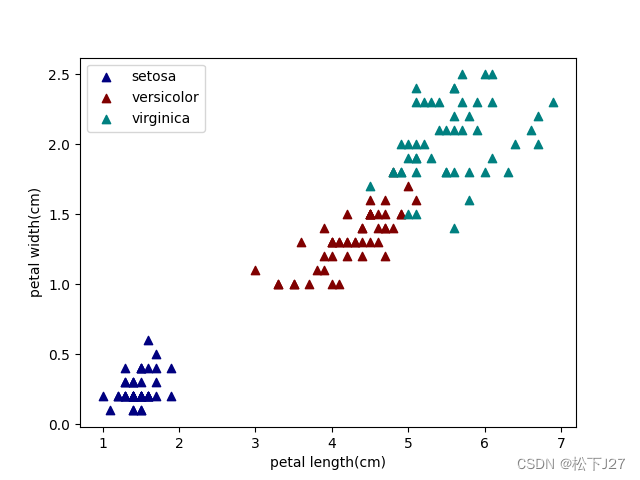
花萼feature的散点图
花萼也一样,virginica维吉尼亚鸢尾花的花萼和versicolor变色鸢尾花的花萼都比setosa山鸢尾的花萼大的多,而且,virginica维吉尼亚鸢尾花的花萼也比versicolor变色鸢尾花的略大一些。
如果把花瓣和花萼的散点图放到一起比较呢,花萼的散点图数据比较集中,彼此之间分的比较开。而花瓣的散点图则比较分散,连在一起的比较多。
4,分别基于花瓣和花萼去构建kNN分类器
导入neighbor分类器
#导入sklearn中的Nearest Neighbors类,它属于sklearn中的classification的大类,属于Supervised learning。
from sklearn import neighbors创建两个分类器
#构造一个kNN分类器
#n_neighbors:指定要考虑的最近邻的数量 k,也就是kNN算法中的k。一般是一个奇数,因为是要用于投票的。且,一般推荐值是数据长度的平方根。
#weights:指定近邻的权重,可以是 'uniform'(所有近邻权重都一样)或 'distance'(分类器会根据邻居点到查询点的距离的倒数来赋予邻居点权重,距离越近的邻居点权重越大)。
#algorithm:指定用于计算最近邻的算法,例如 'auto'、'ball_tree'、'kd_tree' 或 'brute'。
#metric:用于计算邻居之间距离的距离度量。在这里,'minkowski' 是一种常见的距离度量,通常用于欧几里得距离和曼哈顿距离等。
#p: 用于 Minkowski 距离的参数 p。当 p=2 时,Minkowski 距离等同于欧几里得距离。
k=5
clf_sepal=neighbors.KNeighborsClassifier(n_neighbors=k,algorithm="kd_tree",weights="uniform",metric="minkowski",p=2)
clf_petal=neighbors.KNeighborsClassifier(n_neighbors=k,algorithm="kd_tree",weights="uniform",metric="minkowski",p=2)
我们这里所使用的分类器是KNeighborsClassifier,貌似这个东西的中文名字叫k近邻分类器。而且这个分类器的名字也在一定程度上体现了他的分类原理。kNN的分类原理比较简单,大致如下:
(1),在分类器中导入数据库中已有的不同种类的数据
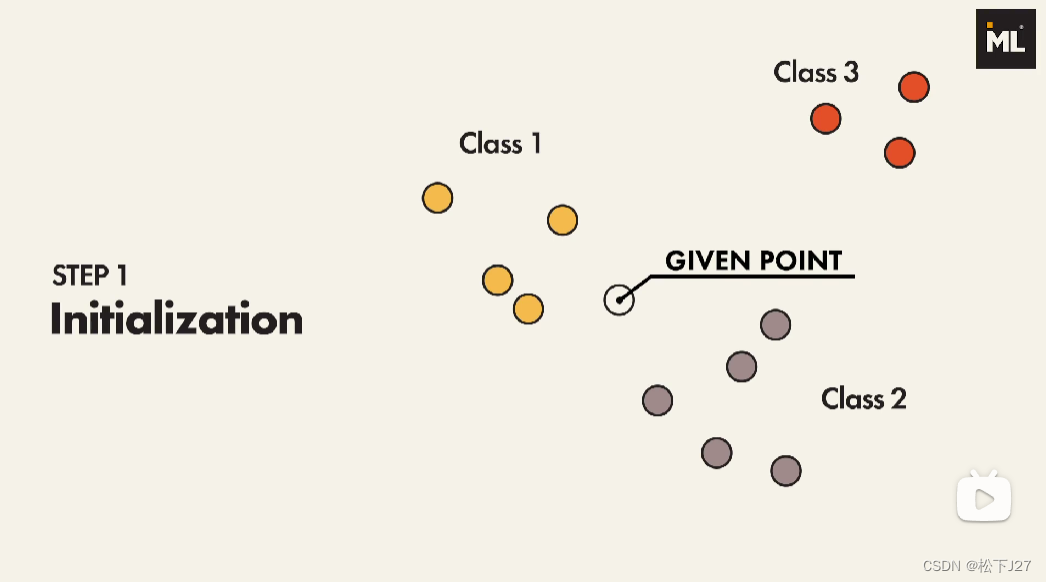
(2),基于你在KNeighborsClassifier分类函数中选择的方式去计算新的数据点(Given point)距离每个点的距离

在neighbors.KNeighborsClassifier函数中,距离的计算方式由参数“metric”和“p”共同决定。对于参数“metric”而言,这里我选择默认值'minkowski'。

他的计算方式为:

这里,我选择了计算欧氏距离,即,Euclidean distance。所以,我令第二个参数p=2。

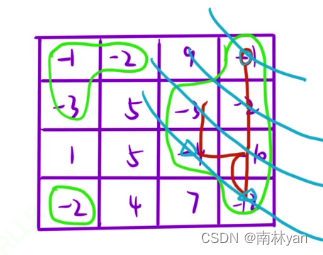
(3),根据前面算出来的欧氏距离按照由近及远的方式对所有参数训练的数据点进行排序。
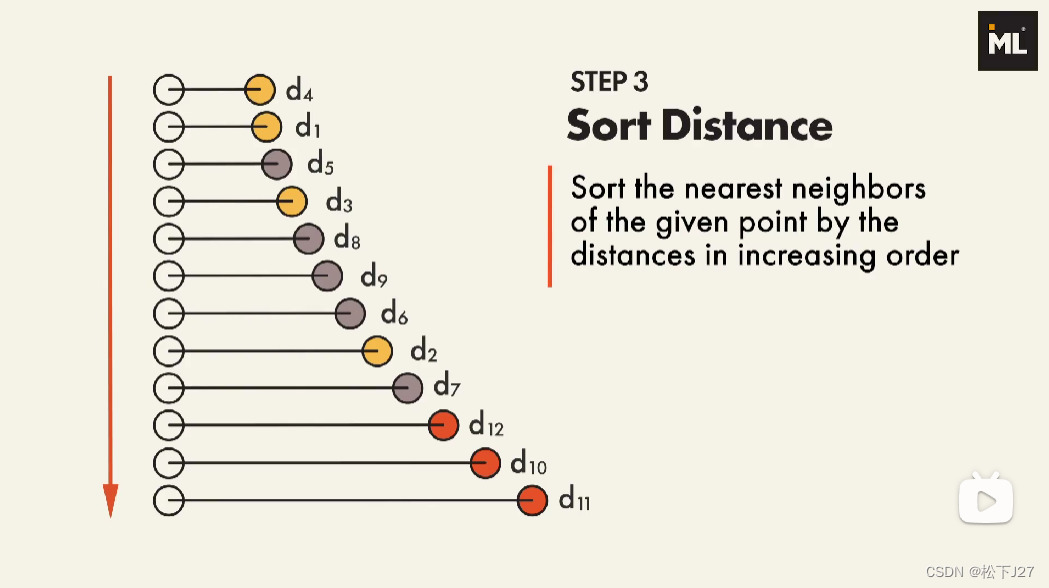
可见,距离given point最近的点是黄色的d4,而最远的是红色的d11。
(4),选择合适的k值,并基于k值分类。(这个k值就是"kNN算法"中的"k")
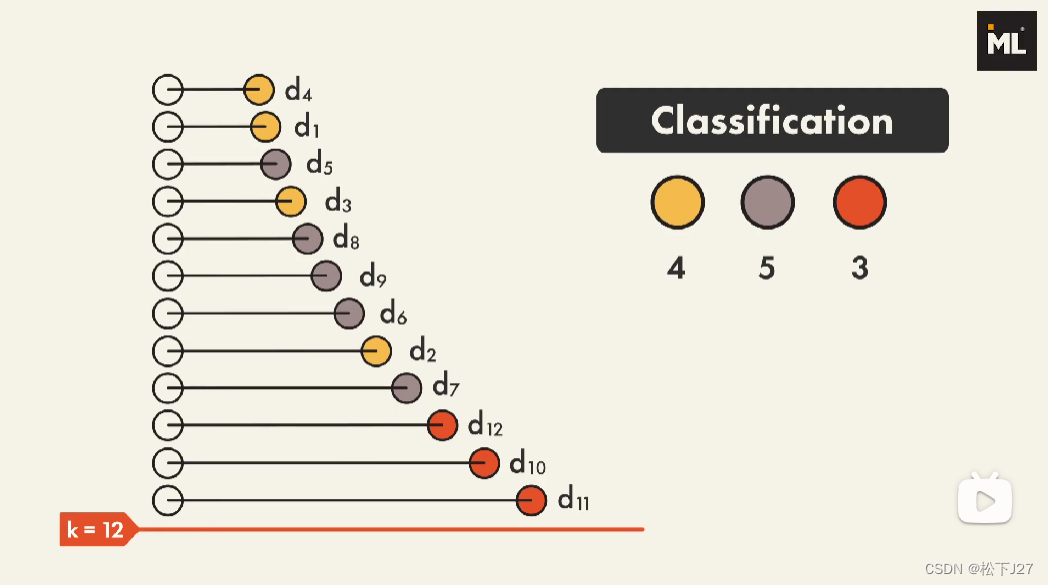
这个k值表示的就是距离新的数据点given point最近的k个点。在neighbors.KNeighborsClassifier函数中,k值用参数“n_neighbors”表示。

如果你希望对新数据点进行分类时,是基于所有的数据点去投票voting。那么你就要把k值设的和你的数据集一样大,例如上图中的k=12。这时,黄圈4票,灰圈5票,红圈3票,基于这个投票结果,given point会被归为灰圈的一类。
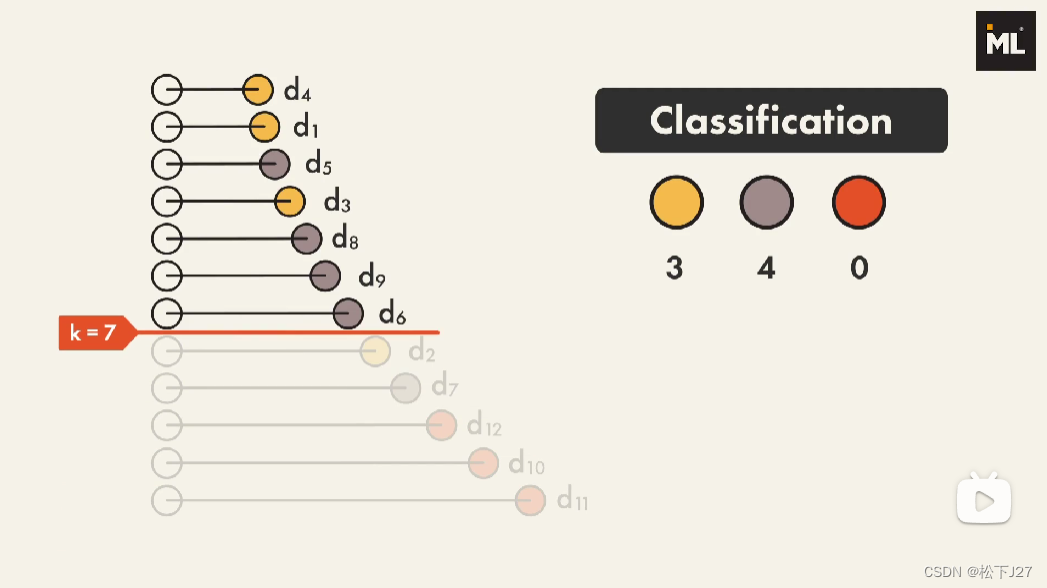
现在把k值改成了7,表示只选择given point邻近的7个数据点voting, 黄圈3票,灰圈4票,红圈0票,given point同样会被归为灰圈一类。
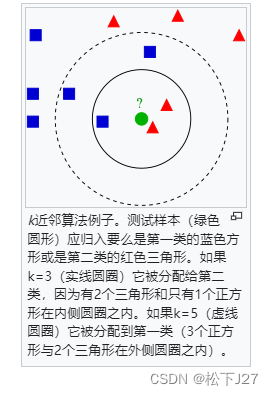
k值的选择是一个需要基于实际情况去权衡利弊的选项。一般情况下,在分类时较大的K值能够减小噪声的影响,但会使类别之间的界限变得模糊。下图就是wiki中关于不同k值的说明图示,中心处的绿点是Given point,如果k=3,投票结果就属于红三角。如果k=5,则投票结果等于蓝方块。
对于kNN原理不太了解的可以看看下面这个视频,视频不长,用动画解释的非常形象生动:
一个非常好的关于机器学习的kNN算法的动画演示(油管搬运)_哔哩哔哩_bilibili
除此之外,KNeighborsClassifier函数中还有两个比较重要的参数:“weights”和“algorithm”,下面是关于这两个参数的相关介绍。

在投票时,k附近的点可以是相同权重的(也就是上图中的方式),也可以使用加权的方式。在neighbors.KNeighborsClassifier函数中对应的参数是“weights”,供了两种选择:'uniform'和'distance'。'uniform'就是相同权重,'distance'就是离得越近权重越高,离得越远权重越小。
kNN分类器的核心是基于given point的k个邻近点的类型去voting,但要找到距离新数据点最近的k个邻居,可以有很多方法/算法。这里的“algorithm”就是专门用来选择寻找k个近邻的算法的配置参数。这里我们用的是'kd_tree'算法,KD-tree算法就是提前对我们的数据集中的数据在数据空间上进行逐级二分,得到多个子空间,也叫leaf叶子。
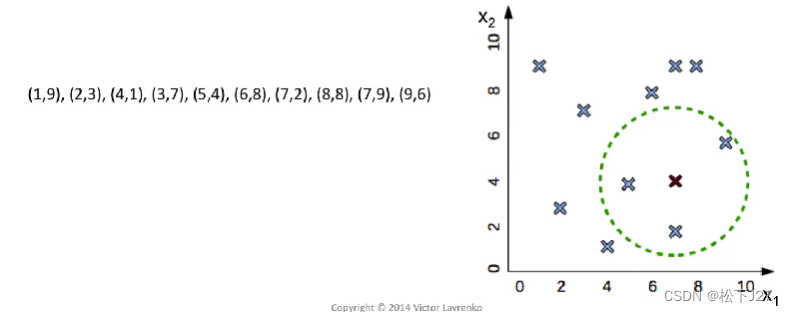
换句话说,KD-tree就是对现有的数据库中数据进行提前划分,形成了一个新的数据结构。当我们输入一个新的Given-point之后,我们不再需要把数据库中的所有点和它的距离算一遍之后再排序,找到前k个近邻。而是,沿着kd-tree的分类方式逐级搜索,每搜索一次,就可以忽略掉一半的数据集,直到找到我们所要的叶子。然后,再在这个叶子中找到离他最近的k个邻居,最后投票分类。
例如下面这一系列的图示所展示的:
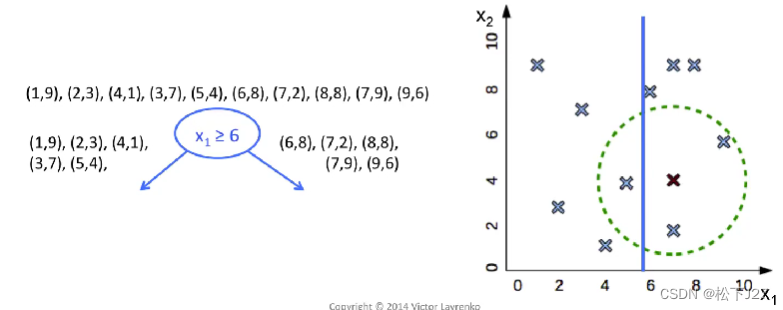
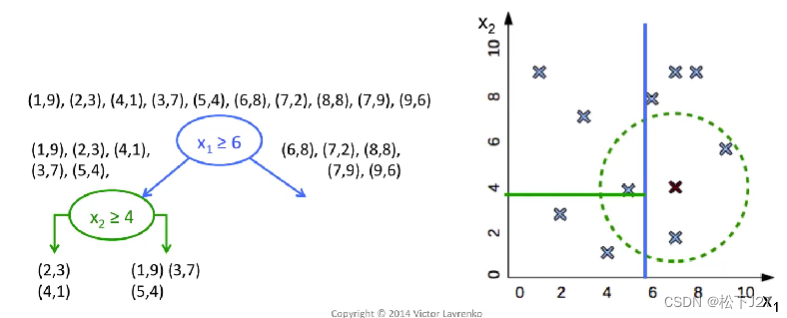
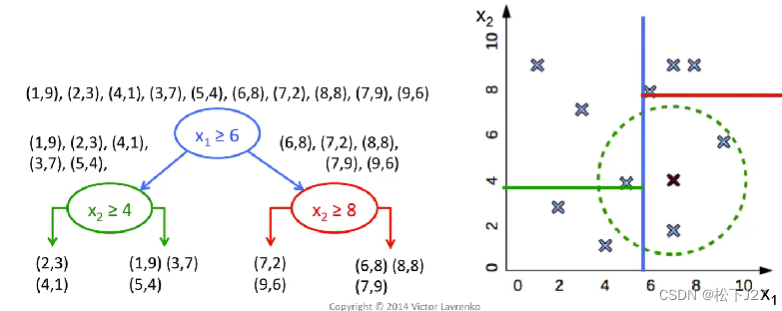
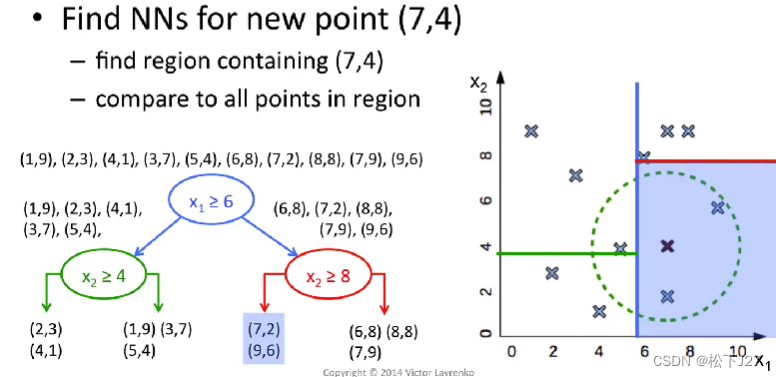
关于KD-Tree的详细的解释可以看看下面这个视频:
kNN算法之Kd tree(油管搬运)_哔哩哔哩_bilibili
5,使用先前构建好的kNN分类器对新数据点Given-point分类
调用函数fit训练数据
#使用分类器对数据进行训练。分类器从训练数据中学习模式和关系,以便后续对新数据进行分类预测。
clf_sepal.fit(x_train_sepal,y_train)
clf_petal.fit(x_train_petal,y_train)6,导入新的数据点Given-Point,并对新数据点进行分类
#输入一组新的数据作为Given-Point
TestData_sepal=[[4.4,1.5]]
TestData_petal=[[3.0,1.8]]
#对新数据的花瓣分类
pred_sepal=clf_sepal.predict(TestData_sepal)
print("classify result of sepal=",pred_sepal)
#对新数据的花瓣分类
pred_petal=clf_petal.predict(TestData_petal)
print("classify result of petal=",pred_petal)我这里的新鸢尾花即给出了它的花瓣数据TestData_sepal,也提供了花萼的数据TestData_petal。分两次调用predict函数进行分类。
7,在之前的散点图绘制Given-Point,并打印分类结果
#把新的数据分别在花瓣和花萼的图像上画出来。
ax_sepal.scatter(TestData_sepal[0][0],TestData_sepal[0][1], c="red",marker='x', label='TestData')
ax_sepal.legend(loc=2)
ax_petal.scatter(TestData_petal[0][0],TestData_petal[0][1], c="red",marker='x', label='TestData')
ax_petal.legend(loc=2)
pred_class1=iris.target_names[pred_sepal]
pred_class2=iris.target_names[pred_petal]
print("pred class of sepal = ",pred_class1)
print("pred class of petal = ",pred_class2)
#stop sign
plt.show()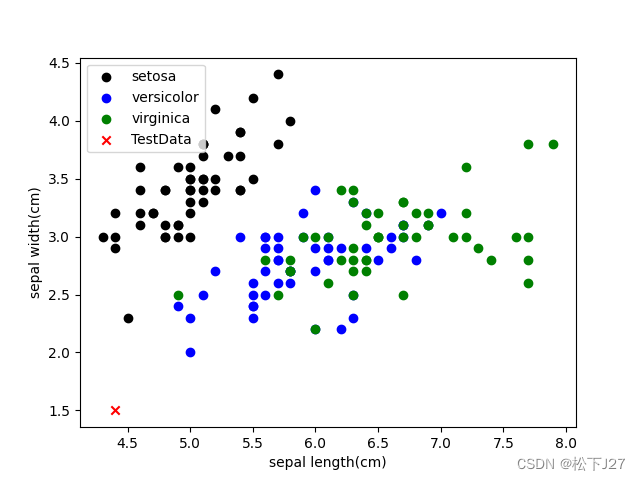
Given-Point在花瓣散点图中的位置
Given-Point在花萼散点图中的位置

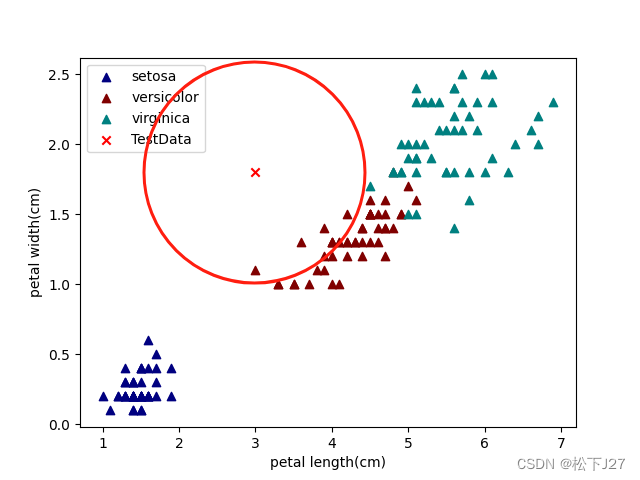
Given-Point基于花瓣和花萼的分类结果
从print的结果中看,当k=5时(也就是选择5个最近的邻居去投票),不论是基于花瓣的尺寸还是基于花萼的尺寸去分类。我们的Given-Point都属于versicolor变色鸢尾花。
在基于花瓣分类的下图中,我手动以given-point为圆心,用圆圈圈出了他的5个近邻。可见,在5个近邻中有一个黑点,一个绿点和三个蓝点,因此,投票结果为versicolor。
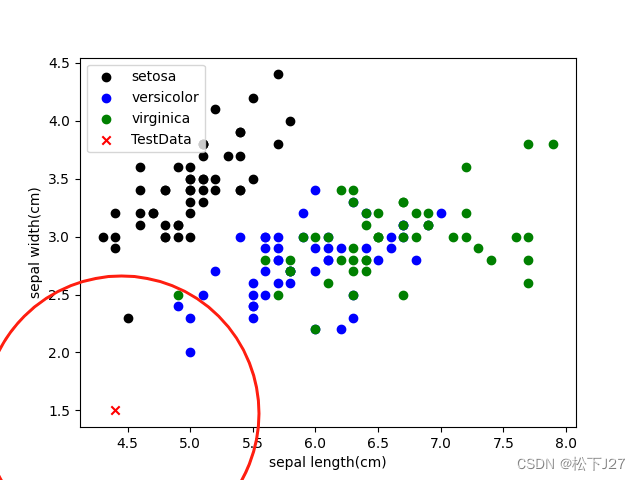
同样,在基于花萼分类的图中,我手动以given-point为圆心,用圆圈圈出了他的5个近邻。可见,在5个近邻都是褐色三角,投票结果为versicolor。
我是一个python+机器学习的小白,这篇文章是我的学习笔记,如文中有错误或有什么不妥的地方望各位看官体谅,谢谢!
(全文完)
作者 --- 松下J27
参考文献(鸣谢):
1,https://en.wikipedia.org/wiki/Iris_flower_data_set
2,https://en.wikipedia.org/wiki/Iris_setosa
3,https://en.wikipedia.org/wiki/Iris_virginica
4,https://en.wikipedia.org/wiki/Iris_versicolor
5,机器学习中的kNN及其Python实例_CSDN博客
6,https://zh.wikipedia.org/wiki/%E5%B1%B1%E9%B8%A2%E5%B0%BE
7,https://zh.wikipedia.org/wiki/%E5%8F%98%E8%89%B2%E9%B8%A2%E5%B0%BE
8,https://peaceadegbite1.medium.com/iris-flower-classification-60790e9718a1
9,https://gist.github.com/curran/a08a1080b88344b0c8a7#file-iris-csv
10,https://commons.wikimedia.org/wiki/File:Flores_de_%C3%8Dris.png
11,https://www.youtube.com/watch?v=0p0o5cmgLdE
12,https://zh.wikipedia.org/wiki/K-%E8%BF%91%E9%82%BB%E7%AE%97%E6%B3%95

(配图与本文无关)
版权声明:文中的部分图片,文字或者其他素材,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27