思路：本题思路比较容易想，主要对于5,10,20三种情况分别讨论，维护三个变量分别记录目前手中三种钞票的数量。bill为5的时候直接收下即可，10的时候，,找零一个5，这两种情况都是固定的。只有遇到20的时候，我们优先使用10来找零，因为5更加万能，只有没有10的时候我们才会找零三张5。**注意顾客排队顺序，必须一个个处理，不能先收后面的钱再整体找零！**时间复杂度O(n)。

class Solution {
public:
    bool lemonadeChange(vector<int>& bills) {
        int five=0,ten=0,twenty=0;
        for(int bill:bills){
            if(bill==5){
                five++;
            }
            else if(bill==10){
                if(five<=0){
                    return false;
                }
                else{
                    five--;
                    ten++;
                }
            }
            else{
                if(ten>0){
                    ten--;
                    twenty++;
                    if(five>0){
                        five--;
                    }
                    else{
                        return false;
                    }
                }
                else{
                    if(five<3){
                        return false;
                    }
                    else{
                        five-=3;
                        twenty++;
                    }
                }
            }
        }
        return true;
    }
};

本题实际上就是顺着正常收钱的思路思考就行，只有找零20的时候是贪心。看标答还可以稍微简化一下：

class Solution {
public:
    bool lemonadeChange(vector<int>& bills) {
        int five = 0, ten = 0, twenty = 0;
        for (int bill : bills) {
            // 情况一
            if (bill == 5) five++;
            // 情况二
            if (bill == 10) {
                if (five <= 0) return false;
                ten++;
                five--;
            }
            // 情况三
            if (bill == 20) {
                // 优先消耗10美元，因为5美元的找零用处更大，能多留着就多留着
                if (five > 0 && ten > 0) {
                    five--;
                    ten--;
                    twenty++; // 其实这行代码可以删了，因为记录20已经没有意义了，不会用20来找零
                } else if (five >= 3) {
                    five -= 3;
                    twenty++; // 同理，这行代码也可以删了
                } else return false;
            }
        }
        return true;
    }
};

思路：本题想了很久没有思路，直接看解答。**本题的队列不是单独按照身高排的，而是预先按照一个固定顺序排好的队列，然后根据h求出对应的k，再将其打乱即为本题的输入。**本题的排序，需要同时考虑k和h，有两个维度，如果先考虑k，排好后没有一个维护确定下来，故先考虑h，根据身高先从大到小排（因为k是求的前面比自己大于等于的身高数量），如果h相同则将k小的放在前面。这样初步排好后，前面的必定比后面高，然后再根据k为下标重新插入队列即可，这样后续插入的节点也不会影响队列，如图所示。时间复杂度O(nlogn+n^2)。

关键点就在根据k为下标插入时，由于前面的h一定比后面大，在插入时，下标恰好就是前面比后面大的个数，这样就完成了复原。

class Solution {
public:
    static bool cmp(vector<int>& v1,vector<int>& v2){//初步排序
        if(v1[0]==v2[0]) return v1[1]<v2[1];//身高相同k小的排前面
        return v1[0]>v2[0];//身高从高到低
    }
    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
        sort(people.begin(),people.end(),cmp);
        vector<vector<int>> ans;
        for(auto v:people){
            ans.insert(ans.begin()+v[1],v);//在位置k处插入，insert的时间复杂度为O(n)
        }
        return ans;
    }
};

时间复杂度主要用于insert，这里如果使用链表list会快很多。但是我没用过list，正常就用链表就OK了。

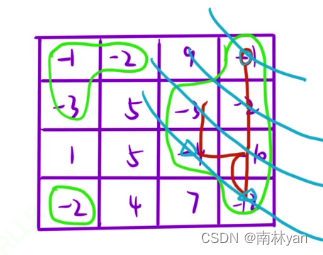
思路：贪心思路就是一开始就射重复最多的气球，举反例没有一开始少射还能用箭最少的，故本题满足局部最优即为全局最优。主要在于实现的时候，如何用代码写出气球重合，气球射爆的过程？首先排序，这里使用起始位置排序，后面射的时候就从左往右遍历。遇到重复气球，那么重叠气球中最右边界的最小值一定需要一个箭，如图所示。

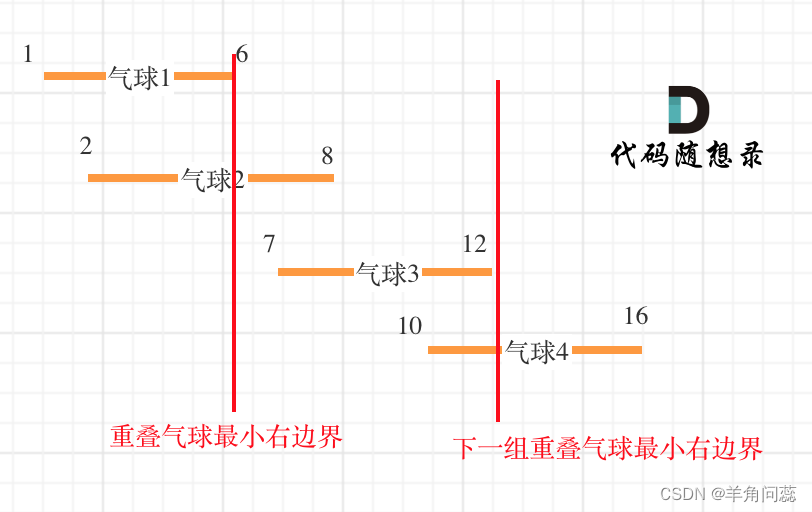
代码的核心就是当气球重叠时，需要更新重叠气球的最小右边界。当下一个气球的左边界大于上一个气球（上一组重合气球）的最小右边界时，即不相交，这时需要额外增加一个箭。时间复杂度O(nlogn)。

class Solution {
private:
    static bool cmp(const vector<int>& a, const vector<int>& b) {
        return a[0] < b[0];//按照起始位置从小到大排序
    }
public:
    int findMinArrowShots(vector<vector<int>>& points) {
        if (points.size() == 0) return 0;
        sort(points.begin(), points.end(), cmp);

        int result = 1; // points 不为空至少需要一支箭
        for (int i = 1; i < points.size(); i++) {
            if (points[i][0] > points[i - 1][1]) {  // 气球i和气球i-1不挨着，注意这里不是>=
                result++; // 需要一支箭
            }
            else {  // 气球i和气球i-1挨着
                points[i][1] = min(points[i - 1][1], points[i][1]); // 更新重叠气球最小右边界
            }
        }
        return result;
    }
};

本题就难在写代码的过程。