c++ 线性搜索与二分搜索

news2024/9/30 7:16:12

线性搜索
假设该项目以随机顺序存在于数组中，并且我们必须找到一个项目。那么搜索目标项目的唯一方法就是从第一个位置开始，并将其与目标进行比较。如果项目相同，我们将返回当前项目的位置。否则，我们将转移到下一个位置。如果我们到达数组的最后一个位置但仍然找不到目标，则返回 -1。这称为线性搜索或顺序搜索。

以下是线性搜索的代码语法：

// Linear Search in C++

#include <iostream>
using namespace std;

int search(int array[], int n, int x)
{

// Going through array sequencially
for (int i = 0; i < n; i++)
if (array[i] == x)
return i;
return -1;
}

二分查找
然而，在二分搜索中，一旦找到排序列表的中间，就将搜索量减少一半。查看中间元素以检查它是否大于或小于要搜索的值。因此，对给定列表的任一半进行搜索

下面是二分查找的代码语法：
#include <iostream>
using namespace std;

int binarySearch(int array[], int x, int low, int high)
{

// Repeat until the pointers low and high meet each
// other
while (low <= high) {
int mid = low + (high - low) / 2;

if (array[mid] == x)
return mid;

if (array[mid] < x)
low = mid + 1;

else
high = mid - 1;
}

return -1;
}

重要差异

线性搜索	二分查找
在线性搜索中，输入数据不需要排序。	在二分查找中，输入数据需要按排序顺序。
它也称为顺序搜索。	也称为半区间搜索。
线性搜索的时间复杂度O(n)。	二分查找的时间复杂度为O(log n)。
可以使用多维数组。	仅使用一维数组。
线性搜索执行相等比较	二分查找执行排序比较
它不太复杂。	它更复杂。
这是一个非常缓慢的过程。	这是一个非常快的过程。

让我们看一个例子来比较两者：

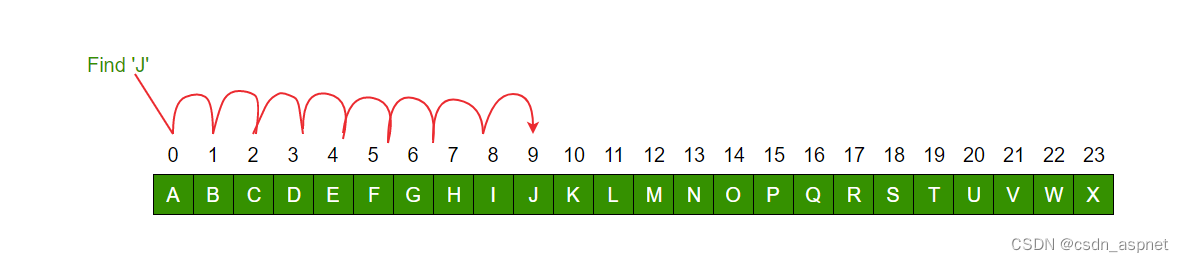
线性搜索从 AX 中查找给定排序列表中的元素“J”

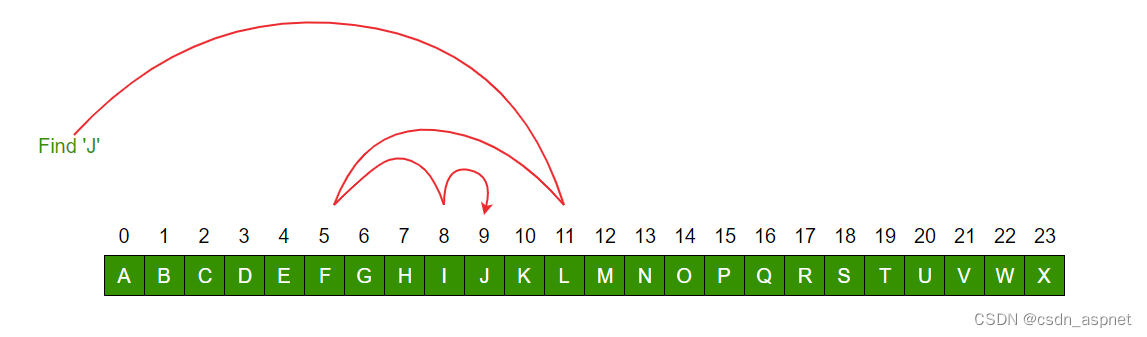
二分查找从 AX 中查找给定排序列表中的元素“J”

线性搜索示例：

#include <iostream>
using namespace std;

int search(int array[], int n, int x)
{

// Going through array sequencially
for (int i = 0; i < n; i++)
if (array[i] == x)
return i;
return -1;
}

int main()
{
int array[] = { 12, 114, 0, 4, 9 };
int x = 4;
int n = sizeof(array) / sizeof(array[0]);

int result = search(array, n, x);

(result == -1)
? cout << "Element not found"
: cout << "Element found at index: " << result;
}

输出
在索引处找到的元素：3
时间复杂度： O(n)，其中 n 是输入数组的大小。最坏的情况是数组中不存在目标元素，并且该函数必须遍历整个数组才能找出该元素。
辅助空间： O(1)，函数仅使用恒定量的额外空间来存储变量。使用的额外空间量不取决于输入数组的大小。

二进制搜索示例：

#include<bits/stdc++.h>
using namespace std;

int binarySearch(vector<int> arr,int x,int low,int high){

while(low <= high){

int mid = low + (high - low)/2;

if (arr[mid] == x)
return mid;

else if (arr[mid] < x)
low = mid + 1;
else
high = mid - 1;
}

return -1;
}

int main(){
vector<int> arr = {2, 4, 5, 7, 14, 17, 19, 22};
int x = 22;

int result = binarySearch(arr, x, 0, arr.size()-1);

if (result != -1)
cout << result << endl;
else
cout << "Not found" << endl;
return 0;
}

// The code is constributed by Nidhi goel