LCR 073. 爱吃香蕉的狒狒

题目

狒狒喜欢吃香蕉。这里有 N 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警卫已经离开了，将在 H 小时后回来。

狒狒可以决定她吃香蕉的速度 K （单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 K 根。如果这堆香蕉少于 K 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉，下一个小时才会开始吃另一堆的香蕉。  

狒狒喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。

返回她可以在 H 小时内吃掉所有香蕉的最小速度 K（K 为整数）。

示例 1：

输入: piles = [3,6,7,11], H = 8
输出: 4

示例 2：

输入: piles = [30,11,23,4,20], H = 5
输出: 30

示例 3：

输入: piles = [30,11,23,4,20], H = 6
输出: 23

提示：

• 1 <= piles.length <= 10^4
• piles.length <= H <= 10^9
• 1 <= piles[i] <= 10^9

思路

二分答案

1. 首先确定答案的区间范围
2. 然后根据题目建立check函数
3. 然后不断对答案区间进行二分找到符合题目的答案 

代码

bool check(int* piles, int pilesSize, int h, int mid) {
    long int sum = 0;
    for (int i = 0; i < pilesSize; i++) {
        sum += (piles[i] + mid - 1) / mid;
    }
    return sum <= h;
}
int minEatingSpeed(int* piles, int pilesSize, int h) {
    int l = 1;
    int r = 0;
    for (int i = 0; i < pilesSize; i++) {
        if (piles[i] >= r)
            r = piles[i];
    }
    int ans = 0;
    while (l <= r) {
        int mid = (r + l) / 2;
        if (check(piles, pilesSize, h, mid)) {
            ans = mid;
            r = mid - 1;
        } else {
            l = mid + 1;
        }
    }
    return ans;
}

64. 最小路径和

题目

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

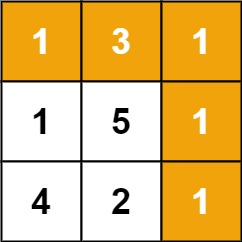
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 200

思路

定义 dp[i] [j]的含义为：

• 当机器人从左上角走到(i, j) 这个位置时，最下的路径和是 dp[i] [j]

找出关系数组元素间的关系式：

• 由于机器人可以向下走或者向右走，所以有两种方式到达
• 一种是从 (i-1, j) 这个位置走一步到达
• 一种是从(i, j - 1) 这个位置走一步到达
• 题目是计算哪一个路径和是最小的，那么我们要从这两种方式中，选择一种，使得dp[i] [j] 的值是最小的，显然有dp[i] [j] = min(dp[i-1][j]，dp[i][j-1]) + arr[i][j];

找出初始值：

最上面一行，机器人只能一直往左走：dp[0] [j] = arr[0] [j] + dp[0] [j-1];

最左面一列，机器人只能一直往下走：dp[i] [0] = arr[i] [0] + dp[i] [0];

代码

int minPathSum(int** grid, int gridSize, int* gridColSize) {
    int m = *gridColSize;
    int n = gridSize;
    if (m < 0 || n < 0) {
        return 0;
    }
    int dp[m][n];
    dp[0][0] = grid[0][0];
    for (int i = 1; i < m; i++) {
        dp[i][0] = dp[i - 1][0] + grid[i][0];
    }
    for (int i = 1; i < n; i++) {
        dp[0][i] = dp[0][i - 1] + grid[0][i];
    }
    for (int i = 1; i < n; i++) {
        for (int j = 1; j < n; j++) {
            dp[i][j] = fmin(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
        }
    }
    return dp[m - 1][n - 1];
}