AVI树
如果一颗二叉搜索树不平衡,那么搜索效率会受影响
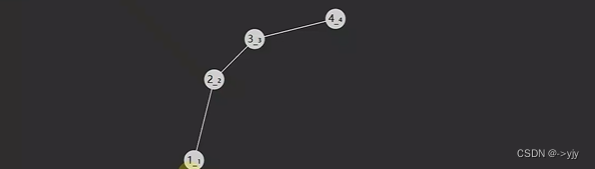
二叉搜索树如果不是这种不平衡的情况,时间复杂度可以达到O(logn) 但是像图中的这种不平衡情况时间复杂度为O(n),那么如何解决呢? 可以通过旋转解决
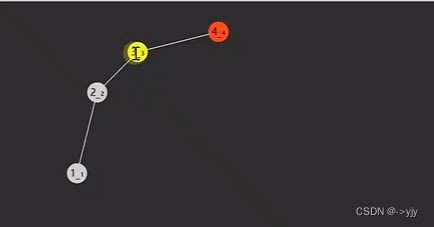
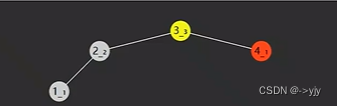旋转之后并不会破坏二叉搜索树的特性
判断是否平衡有一个规则:如果一个节点的左右孩子,高度差超过1,则此节点失衡,才需要旋转
这就是引出这样一棵树:自平衡二叉搜索树
ta的实现有很多种,但其中一种比较著名的实现叫做AVL,为什么叫AVL呢?是因为有两位作者一位取了名字中的AV,另外一个取了L,所以叫AVL树
实现:
/**
* <h3>AVL树</h3>
*
* <ul>
* <li>二叉搜索树在插入和删除时,节点可能失衡</li>
* <li>如果在插入和删除时通过旋转,始终让二叉搜索树保持平衡,称为自平衡的二叉搜索树</li>
* <li>AVL是自平衡二叉树的实现之一</li>
* </ul>
*/
public class AVLTree {
static class AVLNode{
int key;
Object value;
AVLNode left;
AVLNode right;
int height=1;//高度
public AVLNode(int key, Object value) {
this.key = key;
this.value = value;
}
public AVLNode(int key) {
this.key = key;
}
public AVLNode(int key, Object value, AVLNode left, AVLNode right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
// 求节点高度
private int height(AVLNode node){
return node==null?0:node.height;
}
// 更新节点高度(新增,删除,旋转)
private void updateHeight(AVLNode node){
node.height = Integer.max(height(node.left),height(node.right))+1;
}
// 平衡因子(balance factor) = 左子树高度 - 右子树高度
private int bf(AVLNode node){
return height(node.left) - height(node.right);
}
//0 -1 1 平衡的
//> 1 <-1不平衡 bf > 1时,表示左边太高 bf<-1时,表示右边太高
}
求节点高度的时候可以参照前面写过的求二叉树最大深度的题目
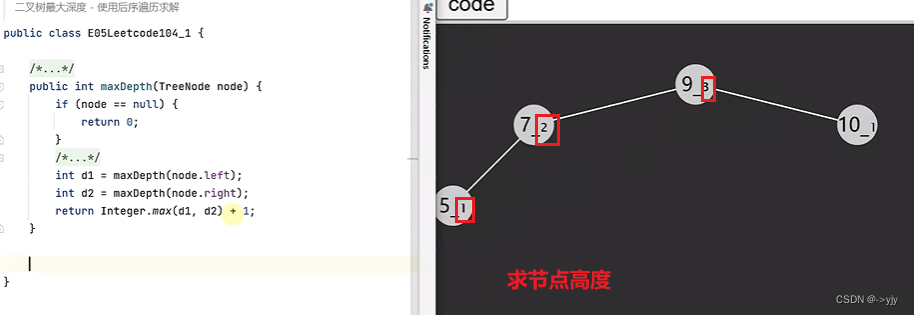
AVI树的旋转
第一种需要旋转的: LL类型
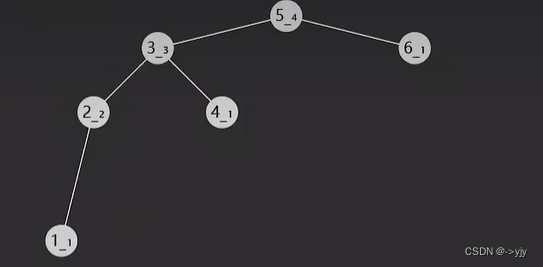
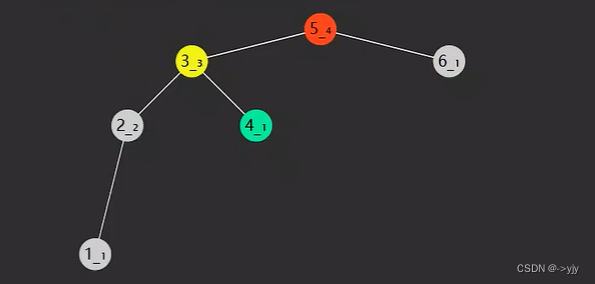
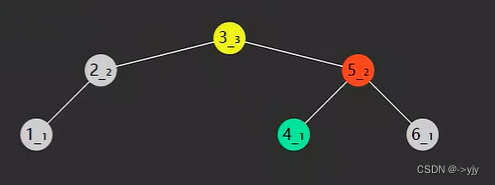
第二种情况:LR类型 -
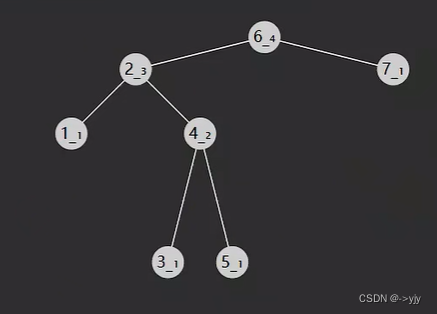
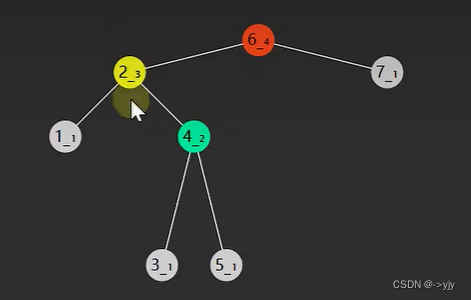
另外两种情况就RR RL 跟上面两种对称
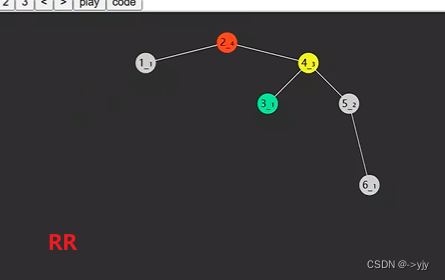
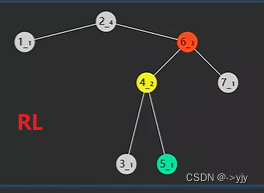
总的来讲: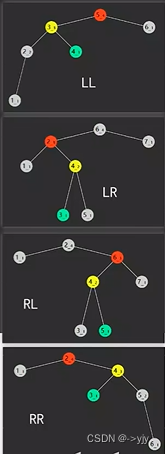
旋转:对于LL就是一次右旋;RR就是一次左旋;LR就是对左子树一次左旋;失衡节点右旋;RL就是对右子树进行一次右旋,失衡节点进行一次左旋;
虽然分了四种情况但是无非也就是左旋和右旋
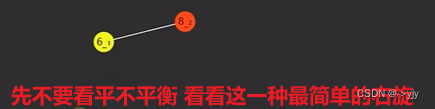
// 参数:要旋转的点,返回值:新的根节点
private AVLNode rightRotate(AVLNode node){//这里的node相当于red
AVLNode left = node.left;//left相当于yellow
left.right = node;
return left;
}相当于:
// 参数:要旋转的点,返回值:新的根节点
private AVLNode rightRotate(AVLNode red){
AVLNode yellow = red.left;
yellow.right = red;
return yellow;
}那来看一种稍微复杂一点的情况: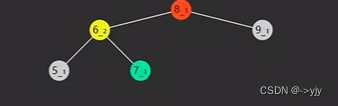
上面的例子中没有考虑黄色节点有右孩子(绿色节点)的情况
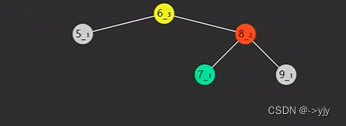
// 参数:要旋转的点,返回值:新的根节点
private AVLNode rightRotate(AVLNode red){
AVLNode yellow = red.left;
AVLNode green = yellow.right;
yellow.right = red; // 上位
red.left=green; // 换爹
return yellow;
}左旋情况: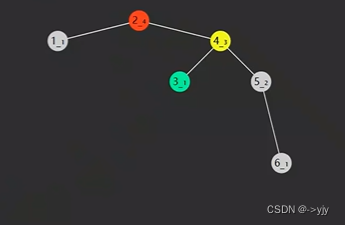
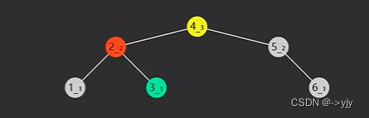
// 参数:要旋转的点,返回值:新的根节点
private AVLNode leftRotate(AVLNode red){
AVLNode yellow = red.right;
AVLNode green = yellow.left;
yellow.left = red;
red.right = green;
return yellow;
}
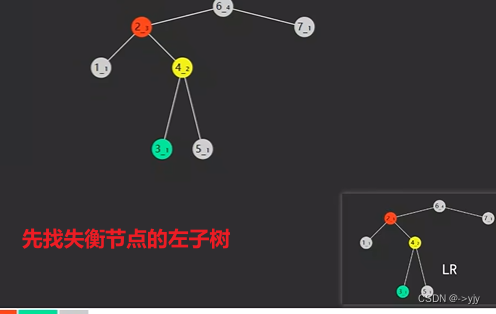
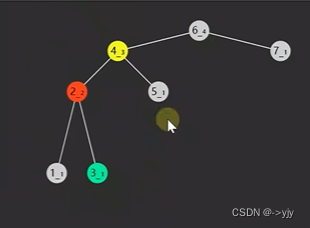
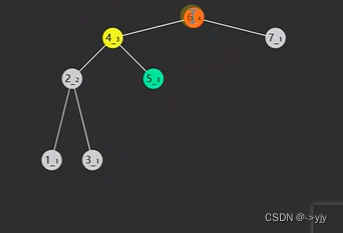
// 先左旋左子树,再右旋根节点 LR
private AVLNode LeftRightRotate(AVLNode node){
node.left = leftRotate(node.left);//左旋完成了
return rightRotate(node);
}
// 先右旋右子树,再左旋根节点
private AVLNode RightLeftRotate(AVLNode node){
node.right = rightRotate(node.right);
return leftRotate(node);
}旋转后节点需要更新
// 参数:要旋转的点,返回值:新的根节点
private AVLNode rightRotate(AVLNode red){
AVLNode yellow = red.left;
AVLNode green = yellow.right;
yellow.right = red; // 上位
red.left=green; // 换爹
updateHeight(red);//不带颜色的节点颜色都不会变 和 绿色也不会变
updateHeight(yellow);
return yellow;
}
// 参数:要旋转的点,返回值:新的根节点
private AVLNode leftRotate(AVLNode red){
AVLNode yellow = red.right;
AVLNode green = yellow.left;
yellow.left = red;
red.right = green;
updateHeight(red);//不带颜色的节点颜色都不会变 和 绿色也不会变
updateHeight(yellow);//这两行不能调位置
return yellow;
}基于以上的实现,我们可以写一个方法检查节点是否失衡,重新平衡代码
// 检查节点是否失衡,重新平衡代码
private AVLNode balance(AVLNode node){
if(node==null){
return null;
}
int bf = bf(node);
if(bf>1 && bf(node.left)>0){//LL
return rightRotate(node);
}else if(bf>1&&bf(node.left)<0){//LR
return LeftRightRotate(node);
}else if(bf<-1 && bf(node.right)>0){//RL
return RightLeftRotate(node);
}else if(bf<-1&&bf(node.right)>0){//RR
return leftRotate(node);
}
return node;
}
但是有两种情况无法处理:发生在删除中
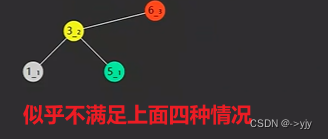但其实一次右旋即可 所以应该是
最终代码:
// 检查节点是否失衡,重新平衡代码
private AVLNode balance(AVLNode node){
if(node==null){
return null;
}
int bf = bf(node);
if(bf>1 && bf(node.left)>=0){//LL
return rightRotate(node);
}else if(bf>1&&bf(node.left)<0){//LR
return LeftRightRotate(node);
}else if(bf<-1 && bf(node.right)>0){//RL
return RightLeftRotate(node);
}else if(bf<-1&&bf(node.right)<=0){//RR
return leftRotate(node);
}
return node;
}新增
AVLNode root;
public void put(int key,Object value){
root = doPut(root,key,value);
}
private AVLNode doPut(AVLNode node,int key, Object value){
// 1.找到空位,创建新节点
if(node==null){
return new AVLNode(key,value);//刚创建高度为1
}
// 2.key 已存在, 更新
if(key == node.key){
node.value = value;
return node;
}
// 3.继续查找
if(key<node.key){
node.left = doPut(node.left,key,value);// 向左
}else{
node.right = doPut(node.right,key,value);// 向右
}
updateHeight(node);
return balance(node);
}
删除
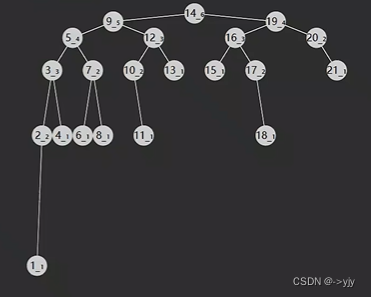
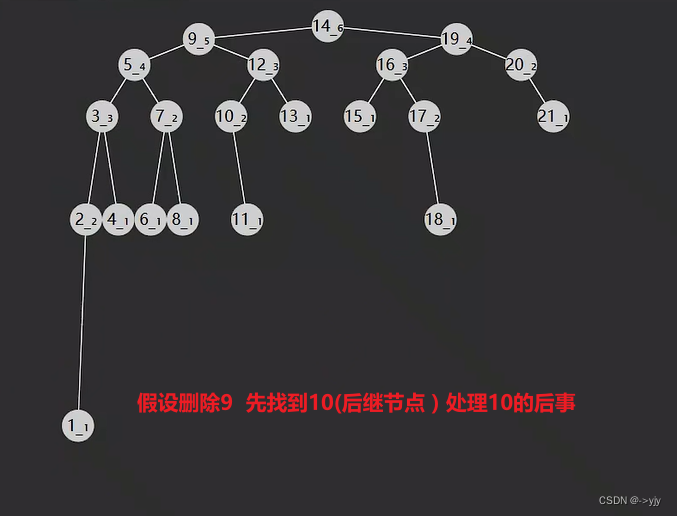
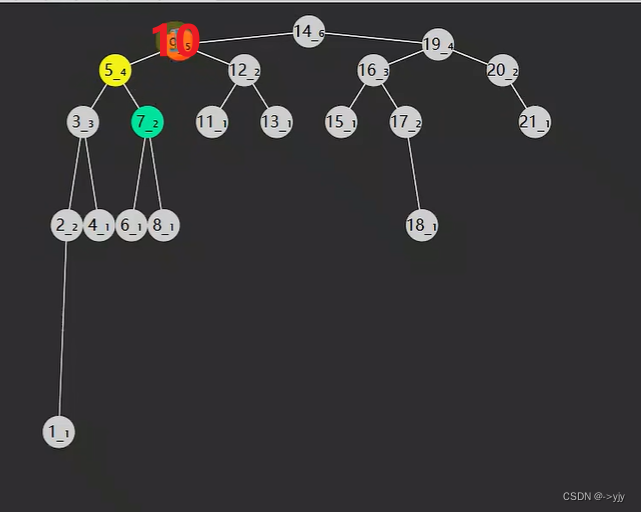
public void remove(int key){
root = doRemove(root,key);
}
private AVLNode doRemove(AVLNode node,int key){
//1.node == null
if(node==null){
return null;
}
//2.没找到key
if(node.key>key){
node.left = doRemove(node.left,key);
}else if(node.key<key){
node.right = doRemove(node.right,key);
}
//3.找到key 1) 没有 2) 只有一个孩子 3) 有两个孩子
else{
if(node.left==null&&node.right==null){
return null;//删剩下的
}else if(node.left==null){
node = node.right;
}else if(node.right==null){
node = node.left;
}else{
//找后继
AVLNode s = node.left;
while(s.left!=null){
s= s.left;
}
//s:后继节点
//处理后继节点后事
s.right = doRemove(node.right,s.key);
s.left =node.left;
node = s;
}
}
//4.更新高度
updateHeight(node);
//5.检查失衡balance
return balance(node);
}
AVI树完整代码
/**
* <h3>AVL树</h3>
*
* <ul>
* <li>二叉搜索树在插入和删除时,节点可能失衡</li>
* <li>如果在插入和删除时通过旋转,始终让二叉搜索树保持平衡,称为自平衡的二叉搜索树</li>
* <li>AVL是自平衡二叉树的实现之一</li>
* </ul>
*/
public class AVLTree {
static class AVLNode{
int key;
Object value;
AVLNode left;
AVLNode right;
int height=1;//高度
public AVLNode(int key, Object value) {
this.key = key;
this.value = value;
}
public AVLNode(int key) {
this.key = key;
}
public AVLNode(int key, Object value, AVLNode left, AVLNode right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
// 求节点高度
private int height(AVLNode node){
return node==null?0:node.height;
}
// 更新节点高度(新增,删除,旋转)
private void updateHeight(AVLNode node){
node.height = Integer.max(height(node.left),height(node.right))+1;
}
// 平衡因子(balance factor) = 左子树高度 - 右子树高度
private int bf(AVLNode node){
return height(node.left) - height(node.right);
}
//0 -1 1 平衡的
//> 1 <-1不平衡 bf > 1时,表示左边太高 bf<-1时,表示右边太高
/*
LL
- 失衡节点的bf>1,即左边更高
- 失衡节点的左孩子的bf>=0,即做孩子这边也是左边更高或等高
LR
- 失衡节点的bf>1,即左边更高
- 失衡节点的做孩子的bf<0,即做孩子这边是右边更高
RL
- 失衡节点的bf<-1,即右边更高
- 失衡接地那的右孩子的bf>0,即右孩子这边左边更高
RR
- 失衡节点的bf<-1,即右边更高
- 失衡节点的右孩子的bf<=0,即右孩子这边右边更高或等高
*/
// 参数:要旋转的点,返回值:新的根节点
private AVLNode rightRotate(AVLNode red){
AVLNode yellow = red.left;
AVLNode green = yellow.right;
yellow.right = red; // 上位
red.left=green; // 换爹
updateHeight(red);//不带颜色的节点颜色都不会变 和 绿色也不会变
updateHeight(yellow);
return yellow;
}
// 参数:要旋转的点,返回值:新的根节点
private AVLNode leftRotate(AVLNode red){
AVLNode yellow = red.right;
AVLNode green = yellow.left;
yellow.left = red;
red.right = green;
updateHeight(red);//不带颜色的节点颜色都不会变 和 绿色也不会变
updateHeight(yellow);//这两行不能调位置
return yellow;
}
// 先左旋左子树,再右旋根节点 LR
private AVLNode LeftRightRotate(AVLNode node){
node.left = leftRotate(node.left);//左旋完成了
return rightRotate(node);
}
// 先右旋右子树,再左旋根节点
private AVLNode RightLeftRotate(AVLNode node){
node.right = rightRotate(node.right);
return leftRotate(node);
}
// 检查节点是否失衡,重新平衡代码
private AVLNode balance(AVLNode node){
if(node==null){
return null;
}
int bf = bf(node);
if(bf>1 && bf(node.left)>=0){//LL
return rightRotate(node);
}else if(bf>1&&bf(node.left)<0){//LR
return LeftRightRotate(node);
}else if(bf<-1 && bf(node.right)>0){//RL
return RightLeftRotate(node);
}else if(bf<-1&&bf(node.right)<=0){//RR
return leftRotate(node);
}
return node;
}
AVLNode root;
public void put(int key,Object value){
root = doPut(root,key,value);
}
private AVLNode doPut(AVLNode node,int key, Object value){
// 1.找到空位,创建新节点
if(node==null){
return new AVLNode(key,value);//刚创建高度为1
}
// 2.key 已存在, 更新
if(key == node.key){
node.value = value;
return node;
}
// 3.继续查找
if(key<node.key){
node.left = doPut(node.left,key,value);// 向左
}else{
node.right = doPut(node.right,key,value);// 向右
}
updateHeight(node);
return balance(node);
}
public void remove(int key){
root = doRemove(root,key);
}
private AVLNode doRemove(AVLNode node,int key){
//1.node == null
if(node==null){
return null;
}
//2.没找到key
if(node.key>key){
node.left = doRemove(node.left,key);
}else if(node.key<key){
node.right = doRemove(node.right,key);
}
//3.找到key 1) 没有 2) 只有一个孩子 3) 有两个孩子
else{
if(node.left==null&&node.right==null){
return null;//删剩下的
}else if(node.left==null){
node = node.right;
}else if(node.right==null){
node = node.left;
}else{
//找后继
AVLNode s = node.left;
while(s.left!=null){
s= s.left;
}
//s:后继节点
//处理后继节点后事
s.right = doRemove(node.right,s.key);
s.left =node.left;
node = s;
}
}
//4.更新高度
updateHeight(node);
//5.检查失衡balance
return balance(node);
}
}
