（2024|ICLR，变分扩散模型（VDM），可学习编码器，时间相关的均值函数）DiffEnc：使用学到的编码器进行变分扩散

DiffEnc: Variational Diffusion with a Learned Encoder

公和众和号：EDPJ（进 Q 交流群：922230617 或加 VX：CV_EDPJ 进 V 交流群）

0. 摘要

2. 变分扩散模型的基础

3. DiffEnc

4. 编码器和生成模型的参数化

5. 实验

7. 限制和未来工作

8. 结论

0. 摘要

扩散模型可以被视为具有两个改进的分层变分自动编码器（VAE）：

在生成过程中参数共享的条件分布
在层次结构上独立计算损失的有效性。

我们考虑对扩散模型进行两项改变，保留这些优势的同时增加了模型的灵活性。

首先，我们在扩散过程中引入了一个与数据和深度相关的均值函数，这导致了修改后的扩散损失。我们提出的框架 DiffEnc，在CIFAR-10上实现了显著的似然改进。
其次，我们让逆编码器过程（reverse encoder process）的噪声方差与生成过程的噪声方差之比成为一个自由权重参数，而不是固定为 1。

这导致了理论上的洞察：

对于有限深度的层次结构，证据下界（ELBO）可以用作加权扩散损失方法的目标，并且可以用于专门用于推理的噪声时间表的优化。
对于无限深度的层次结构，权重参数必须为 1 才能具有良好定义的 ELBO。

项目页面：https://github.com/bemigini/DiffEnc

2. 变分扩散模型的基础

我们从介绍扩散模型的 VDM 公式（Kingma等人，2021）开始。我们定义了一个具有 T+1 层潜变量的分层生成模型：

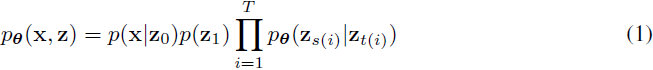
其中，x∈X 是一个数据点，θ 是模型参数，s(i)= (i−1)/T，t(i)=i/T，并且 p(z1)=N(0,I)。在接下来的内容中，我们将去掉索引 i 并假设 0≤s<t≤1。我们定义了一个扩散过程 q 的边缘分布：

其中 t∈[0,1] 是时间索引，αt 和 σt 是 t 的正标量函数。要求等式（2）对任意的 s 和 t 都成立，条件化为：

利用贝叶斯规则，我们可以逆转扩散过程的方向：

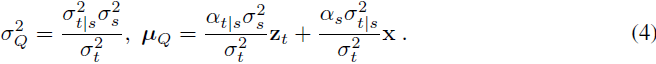
我们现在可以用与公式（1）相同的函数形式表达扩散过程：

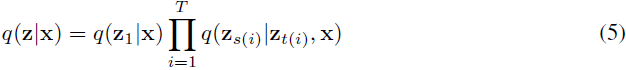
并且我们可以定义与公式（3）相同的生成过程的一步：

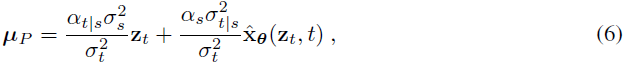
其中 ^xθ 是具有参数 θ 的学到的模型。在扩散模型中，去噪方差 σ^2_P 通常选择与逆扩散过程的方差相等：σ^2_P=σ^2_Q。虽然最初我们不做出这个假设，但我们将证明在连续时间限制下这是最优的。根据 VDM，我们通过信噪比（SNR）来参数化噪声时间表：

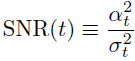
以及它的对数：λt≡logSNR(t)。我们将在所有实验中使用方差保持（VP）的公式：

上述模型的证据下界（ELBO）是：

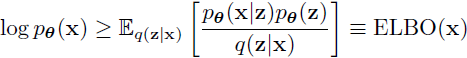
损失函数 L ≡ -ELBO 是重构（L0）、扩散（LT）和潜在（L1）损失的总和：

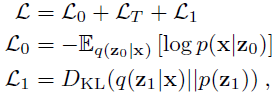
其中，L0 和 L1 的表达式在附录 D 中推导得到。由于生成和逆向噪声过程的匹配因子分解方式（见公式（1）和（5）），以及由于 q 是马尔可夫和高斯的，因此扩散损失 LT 可以写成对随机变量层的求和或期望：

其中，U{1, T} 是 1 到 T 的均匀分布。由于所有分布都是高斯的，KL 散度有一个封闭形式的表达式（见附录 E）：

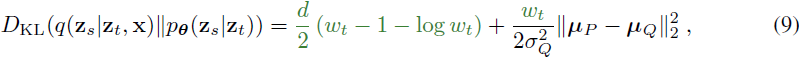
其中，绿色部分是使用 σ^2_P ≠ σ^2_Q 而不是 σ^2_P = σ^2_Q 的差异，我们定义了权重函数

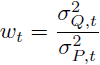
并且 σ^2_(Q ,t) 和 σ^2_(P ,t) 对 s 的依赖性被隐式地留下，因为步长 t−s= 1/T 是固定的。最优生成方差可以通过封闭形式计算（见附录 F）：

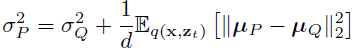
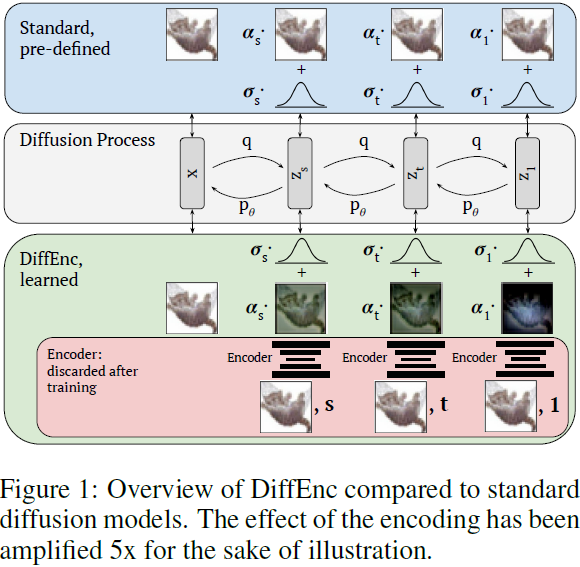
3. DiffEnc

DiffEnc 的主要组成部分是时间依赖的编码器，我们将其定义为 xt ≡ x_ϕ(λt)，其中 xϕ(λt) 是某个具有参数 ϕ 的函数，通过 λt ≡ logSNR(t) 依赖于 x 和 t。然后，公式（2）的广义版本为：

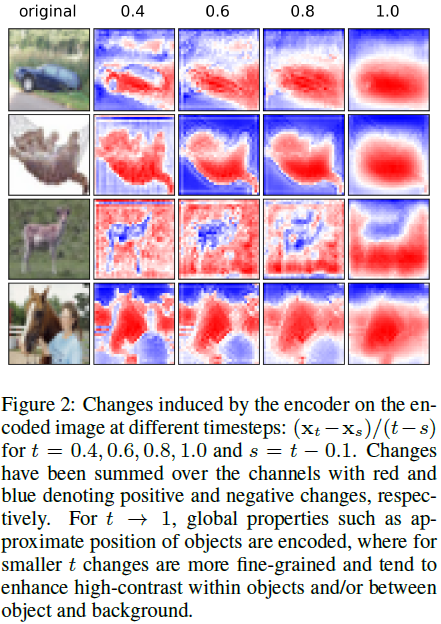
图 1 可视化了扩散过程的这一变化，并在附录 A 中提供了图表。要求过程在边缘化时保持一致，即，

导致以下条件分布（见附录 B）：

其中，深度相关编码器引入了一个额外的均值偏移项（蓝色）。与第 2 节类似，我们可以推导出逆过程（见附录 C）：

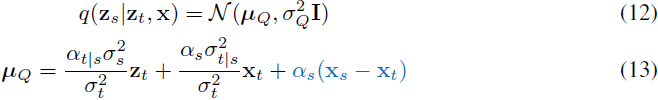
其中，σ^Q_2 由公式（4）给出。我们将在第 4 节中展示如何参数化编码器。

无限深度极限。Kingma 等人（2021年）推导了扩散损失的连续时间极限，即当 T → ∞ 时的损失。我们可以将该结果扩展到我们的情况。使用公式（13）中的 μQ 和公式（6）中的 μP，未加权情况下的 KL 散度，即

可以按照附录 G 中所示的方式重写：

其中，

类似地对于 SNR 也是如此。在附录 G 中，我们还展示了，当 T→∞ 时，最优 σP 的表达式趋向于 σQ，允许 σ^2_P ≠ σ^2_Q 的扩散损失中的额外项趋向于 0。这个结果与先前关于随机过程变分方法的工作（Archambeau等人，2007）一致。我们已经证明，在连续极限中，ELBO 必须是一个未加权损失（即 wt=1）。在本文的其余部分，我们将使用连续的表述，因此设置 wt=1。然而，考虑为有限层数优化加权损失是很有趣的，我们将把这留给将来的研究。

扩散损失的无限深度极限，

变为（见附录 G）：

因此，L∞(x) 非常类似于来自 VDM 的标准连续时间扩散损失，尽管具有来自均值偏移项（蓝色）的额外梯度。在第 4 节中，我们将开发一个修改后的生成模型来对抗这个额外项。在附录 H 中，我们推导了描述 DiffEnc 生成模型在无限深度极限下的随机微分方程（SDE）。

4. 编码器和生成模型的参数化

现在我们转向对编码器 xϕ(λt) 的参数化。重构和潜在损失对编码器在潜变量层次结构的两端的行为施加了约束：我们使用的似然性是这样构造的，在 xϕ(λ0) = x 时，重构损失（在附录 D 中推导）被最小化。同样，潜在损失在 xϕ(λ1) = 0 时被最小化。在两者之间，对于 0 < t < 1，一个非平凡的编码器可以改善扩散损失。

我们提出了编码器的两种相关参数化方法：一个是可训练的，我们将其表示为 x_ϕ，另一个是更简单的、不可训练的，记为 x_nt，其中 nt 表示不可训练。设 yϕ(x, λt) 为一个具有参数 ϕ 的神经网络，为简洁起见，记为 yϕ(λt)。我们将可训练的编码器定义为

不可训练的编码器为

这些参数化的更多动机可以在附录 I 中找到。可训练的编码器 xϕ 被初始化为 yϕ(λt) = 0，因此在训练开始时，它起到不可训练的编码器 x_nt 的作用（但与 VDM 不同，VDM 对应于恒等编码器）。

略。

5. 实验

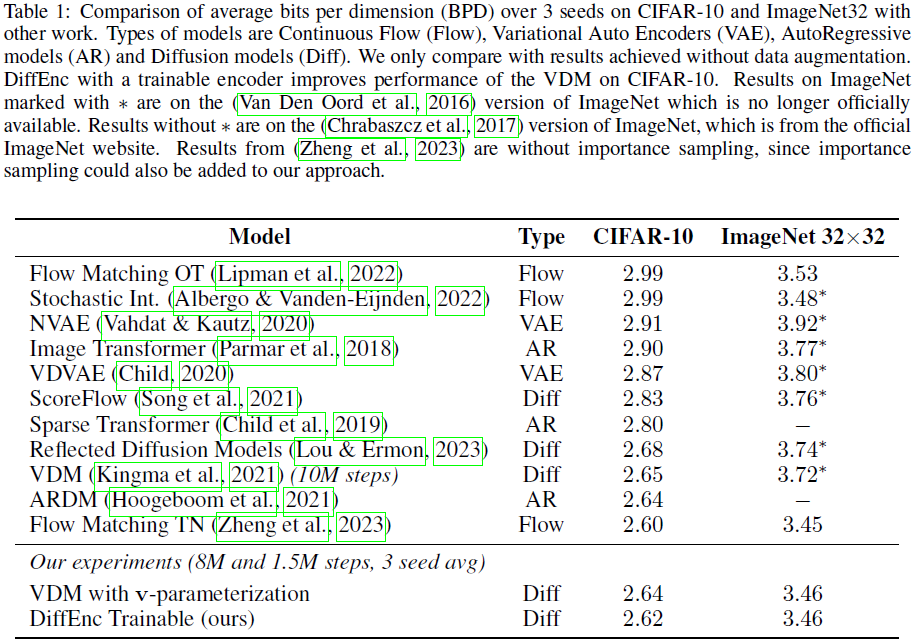
7. 限制和未来工作

如上所示，添加一个经过训练的时间依赖编码器可以提高扩散模型的似然性，但会增加训练时间。尽管我们的方法不会增加采样时间，但必须注意到采样仍然比生成对抗网络（Goodfellow等人，2014年）等方法显著慢。扩散模型中更高效采样的技术（Watson等人，2021年；Salimans & Ho，2022年；Song等人，2020年；Lu等人，2022年；Berthelot等人，2023年；Luhman & Luhman，2021年；Liu等人，2022年）可以直接应用于我们的方法。

引入可训练的编码器为表示学习开辟了一个有趣的新方向。应该可以将时间依赖的转换提炼出来，以获得图像的较小的时间依赖表示。看到这样的表示能告诉我们关于数据的什么信息将是有趣的。此外，探索是否为编码器添加条件会导致不同类别的图像具有不同的变换也是有趣的。

如 (Theis等人，2015年) 所示，样本的似然性和视觉质量并不直接相关。因此，根据模型被训练优化的指标选择应用是很重要的。由于我们展示了我们的模型在被优化为最大化似然性时可以取得良好的结果，并且在半监督学习的背景下似然性很重要，因此使用这种模型进行半监督设置的分类将是有趣的。

8. 结论

我们提出了 DiffEnc，这是扩散模型的一个泛化，其中包含了一个时间依赖的编码器。DiffEnc 增加了扩散模型的灵活性，同时保持了相同的采样计算要求。此外，我们从理论上推导出了生成过程的最优方差，并证明了在连续时间极限下，它必须等于扩散方差，以使 ELBO 有良好定义。我们将其应用于采样或离散时间训练的调查推迟到未来工作。在实证方面，我们展示了 DiffEnc 可以提高 CIFAR-10 的似然性，并且编码器学习的数据转换与时间步长有非平凡的依赖关系。未来研究的有趣途径包括应用改进扩散模型的方法，这些方法与我们提出的方法正交，如潜在扩散模型、模型提炼、无分类器指导和不同的采样策略。