粒子滤波
本文是对于原文的学习与部分的转载
https://blog.csdn.net/weixin_44044161/article/details/125445579
粒子滤波是在目标跟踪中常用的一种方法
非线性条件下,贝叶斯滤波面临一个重要的问题是状态分布的表达与积分式的求解
由前面章节中的分析可以得知,对于一般的非线性系统,解析求解的途径是行不通的
在数值近似方法中,蒙特卡洛方针是一种最为通用与有效的方法
粒子滤波就是建立在蒙特卡罗仿真基础之上的,它通过利用一组带权值的系统状态采样来近似状态的统计分布。
由于蒙特卡罗仿真方法具有广泛的适用性,由此得到的粒子滤波算法也能适用于一般的非线性/非高斯系统。但是,这种滤波方法也面临几个重要问题,如有效采样(粒子)如何产生、粒子如何传递以及系统状态的序贯估计如何得到等。
非线性系统
首先我们了解到非线性的系统
由于我们得到是时间与其相关传感器信息往往是离散的,也就是其往往不是连续变化的,不能使用微分方程来表示,而使用递推公式表示
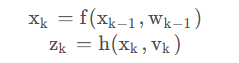
这就是我们所需要的递推公式
其中
x
k
x_k
xk为k时刻的目标状态向量,
z
k
z_k
zk为k时刻的时刻量测向量
w
K
w_K
wK与
v
k
v_k
vk 分别是过程噪声序列和量测噪声序列,均为零均值高斯白噪声。
相当于我们用前一次系统的状态信息与噪声来得到本次的状态信息
由本时刻的状态信息与噪声得到量测向量
因为贝叶斯滤波的递推形式是基于非线性系统的后验概率密度,因此这里并不用假设
w
k
w_k
wk
v
k
v_k
vk为零均值高斯白噪声,而KF、EKF、CKF、QKF等都需要假设过程,测量噪声均为高斯噪声
因此贝叶斯滤波的粒子滤波可以处理非线性非高斯的状态估计问题
贝叶斯滤波的问题就是计算对k时刻x估计的置信程度,为构造概率密度函数,在给定初始分布后从理论上看可以分为预测与更新两个步骤的递推来得到
p
(
x
k
∣
z
k
)
p(x_k|z^k)
p(xk∣zk) 的值
递推贝叶斯滤波
1)预测
现假定k − 1 k- 1k−1时刻的概率密度函数已知,则通过将Chapman-Kolmogorov等式应用
于动态方程(1),即可预测k kk时刻状态的先验概率密度函数为
p
(
x
k
∣
z
k
−
1
)
=
∫
p
(
x
k
∣
x
k
−
1
)
p
(
k
−
1
∣
z
k
−
1
)
d
x
k
−
1
)
\mathbf{p}(\mathbf{x_{k}}|\mathbf{z}^{\mathbf{k}-1})=\int\mathbf{p}(\mathbf{x_{k}}|\mathbf{x_{k}}-1)\mathbf{p}(\mathbf{k}-1|\mathbf{z}^{\mathbf{k}-1})\mathbf{d}\mathbf{x_{k}}-1)
p(xk∣zk−1)=∫p(xk∣xk−1)p(k−1∣zk−1)dxk−1)
实际上,状态转移方程写为概率密度的形式即为:
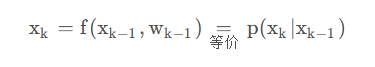
所以我们就得到了预测的函数
2)更新
在获得
p
(
x
k
∣
z
k
−
1
)
p(x_k|z^{k-1})
p(xk∣zk−1)的基础上,结合k时刻得到的新的量测值,基于贝叶斯公式,可以计算k 时刻状态的后验概率密度函数:

式子中
p
(
z
k
∣
z
k
−
1
)
p(z_k|z^{k-1})
p(zk∣zk−1)由全概率公式得到
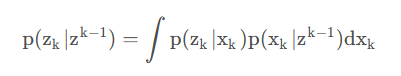
实际上这也是卡尔曼滤波的更新思想,在k时刻测量到
z
k
z_k
zk之后,利用测量
z
k
z_k
zk修正先验概率,进而获得当前时刻状态的后验概率
实际上各种滤波、估计就是求 p ( x k ∣ z k − 1 ) p(x_k|z^{k-1}) p(xk∣zk−1)的一阶矩(x的估计)以及二阶矩(估计的协方)
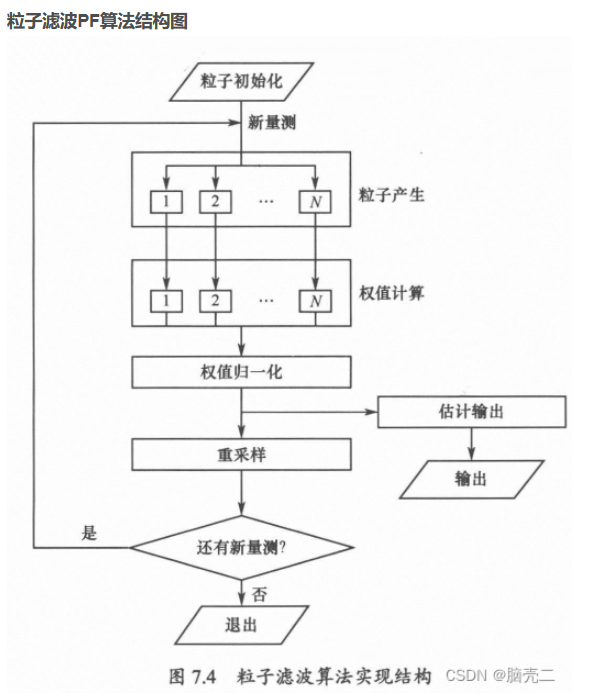
粒子滤波PF
核心思想:是使用一组具有相应权值的随机样本(粒子)来表示状态的后验分布。该方法的基本思路是选取一个重要性概率密度并从中进行随机抽样,得到一些带有相应权值的随机样本后,在状态观测的基础上调节权值的大小和粒子的位置,再使用这些样本来逼近状态后验分布,最后将这组样本的加权求和作为状态的估计值。粒子滤波不受系统模型的线性和高斯假设约束,采用样本形式而不是函数形式对状态概率密度进行描述,使其不需要对状态变量的概率分布进行过多的约束,因而在非线性非高斯动态系统中广泛应用。尽管如此,粒子滤波目前仍存在计算量过大、粒子退化等关键问题亟待突破
粒子滤波实际上是上述基于递推贝叶斯滤波的MMSE(5)估计的近似实现,而近似方法就是蒙特卡洛方法。到这里应该很多人就明白了为什么将粒子滤波都要提及贝叶斯滤波。
通常情况下选择先验分布作为重要性密度函数、即

对该函数取重要性权值为
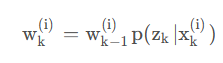
同时需要将
w
k
(
i
)
w_k^{(i)}
wk(i)进行归一化