一、序偶和笛卡尔积
序偶:两个元素按照一定的次序组成的二元组,记为<x,y>,x为第一元素,y为第二元素
序偶的相等条件:<a,b>=<c,d>当且仅当a=c,b=d
n重有序组:n个元素按照一定次序组成的n元组
笛卡尔积:有两个集合A,B,集合A×B={<x,y>|(x∈A)∧(y∈B)} 为A和B的笛卡尔积
笛卡尔积的性质
- 笛卡尔积运算不满足交换律、不满足结合律
- A×B=Ø当且仅当A=Ø,B=Ø
- 若A、B为有限集合,|A×B|=|B×A|=|A|×|B|
- 笛卡尔积对并交运算满足分配律 即A×(B∪C)=(A×B)∪(A×C)
二、关系定义
关系:A、B两个非空集合,A×B的任意子集R为从A到B的一个二元关系,简称关系。A为R的前域,B为R的后域,如果A=B,则R为A上的一个二元关系
R=0,称R为从A到B的空关系。
当R=A×B,称R为从A到B的全关系。A上全关系记为E_A
当R={<x,x>|x∈A}时,称R为A上的恒等关系
关系的定义域和值域
前域中被关系引用到的元素构成定义域
后域中被关系引用到的元素构成值域
定义域和值域的并集合为R的域
如:A={a1,a2,a3} B={b1,b2,b3} R={<a1,b1>,<a1,b2>,<a2,b1>}
则:R的定义域为{a1,a2}值域为{b1,b2}
三、关系的表示
关系的集合表示
- 枚举法(R={<a,b>,<c,d>})
- 叙述法(R={<x,y>|(x,y∈R)∧(x=y)})
关系图表示法
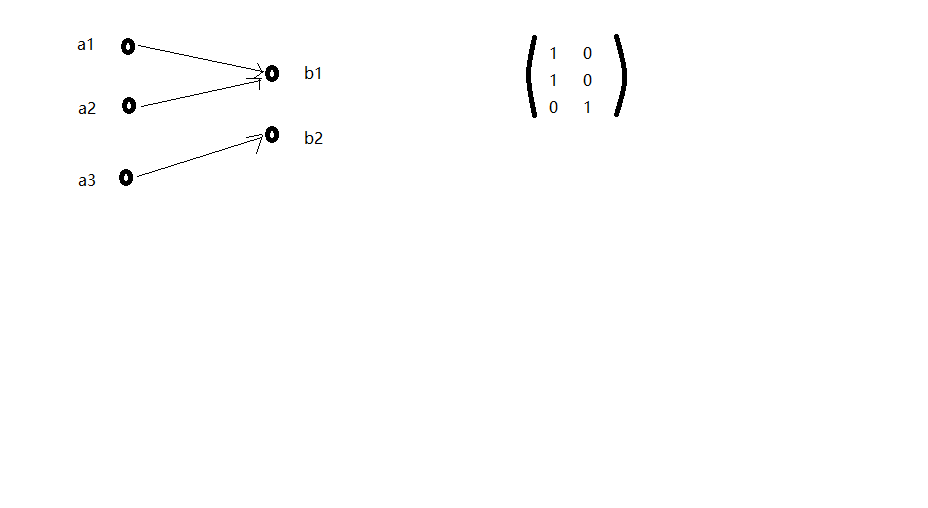
关系矩阵表示
A={a1,a2……an}
B={b1,b2……bm}
MR=(mij)n×m
当<ai,bi>∈R时mij=1 反之mij=0
MR为R的邻接矩阵
布尔矩阵运算
并、交(A、B行数列数相同):按位对应进行运算
积运算(A(m行p列),B(p行n列),结果C(m行n列)):Cij的确定-A的行与B的列对应相按位与,如果结果不为0,则结果为1
四、关系的运算
关系是特殊的集合。集合的所有运算都可以运用到关系中,关系的运算也满足集合运算的定律
复合运算:R:A→B S:B→C R°S={<x,z>|(x∈A)∧(z∈C)∧(∃y)(y∈B∧xRy,ySz)},°称为复合运算
逆运算R-1表示B到A的关系
R-1的关系矩阵是R的关系矩阵的转置
复合运算满足的性质
记R、S、T分别是A到B、B到C、C到D的二元关系
记IA、IBB为A、B上的恒等关系
R°S°T=R°(S°T)
IA°R=R°IB
R°(S1∪S2)=(R°S1)∪(R°S2)
(S1∪S2)°R=(S1°R)∪(S2°R)
R°(S1∩S2)⊆(R°S1)∩(R°S2)
(S1∩S2)°R⊆(S1°R)∩(S2°R)
逆运算满足的性质
并、交、差都满足(R∪S)-1=R-1∪S-1 (R°S)-1=R-1°S-1
R的补-1=R-1的补
(R-1)-1=R
S⊆R↔S-1⊆R-1
关系的幂运算
满足结合律就可以进行幂运算
设R为关系A上的集合
R0=IA
R1=R
Rn+1=Rn°R=R°Rn
幂运算的收敛性A为有限集合|A|=n, R1∪R2……Rn=R1∪R2……R∞
五、关系的性质
设R是集合A上的元素
自反性和反自反性
对于任意的x∈A,都有<x,x>∈R,那么称R在A上是自反的,R具有自反性
对于任意的x∈A,都有<x,x>∉R,那么称R在A上是反自反的,R具有反自反性
存在既不自反也不反自反的关系
关系图中每个节点都自环是自反的,每个节点都不自环是反自反的
关系矩阵的主对角线上全为1是自反的,全为0是反自反的
- 自反:IA⊆R
- 反自反:IA∩R=Ø
对称性和反对称性
对于任意的x,y∈A,如果<x,y>∈R,且<y,x>∈R,则称R是对称的,R具有对称性
对于任意的x,y∈A,如果<x,y>∈R,且<y,x>∈R,仅在x=y下满足,则称R是反对称的,R具有反对称性
关系图中:一对节点间要么有方向相反的两条边要么无边,是对称的;任何一对节点之间至多只有一条边是反对称的
关系矩阵中:对称矩阵对应的关系是对称的
- 对称:R=R-1
- 反对称:R∩R-1⊆IA
传递性
对于任意的x,y,z∈A,若<x,y>∈R,<y,z>∈R,<x,z>∈R,则称R是传递的,R具有传递性
传递:R°R⊆R
保守性
具有特殊性质的关系经过运算后保持原有特殊性质的
- R,S 是自反的,则 R1,R∪S,R∩S,RoS也是自反的
- R,S 是反自反的,则 R-1,R∪S, R∩S, R-S也是反自反的
- R,S是对称的,则 R-1,R∪S,R∩S,R-S 也是对称的
- R,S是反对称的,则 R-1,R∩S,R-S也是反对称的
- R,S是传递的,则 R-1,R∩S也是传递的
逆和交运算可以保持原属性
并只能保持自反、反自反、对称
复合只能保持自反
差可以保持反自反、对称、反对此
闭包
闭包:在给定关系中添加最少的元素,使其具有需要的特殊性质