数据可视化（六）：Pandas爬取NBA球队排名、爬取历年中国人口数据、爬取中国大学排名、爬取sina股票数据、绘制精美函数图像

Tips："分享是快乐的源泉💧，在我的博客里，不仅有知识的海洋🌊，还有满满的正能量加持💪，快来和我一起分享这份快乐吧😊！

喜欢我的博客的话，记得点个红心❤️和小关小注哦！您的支持是我创作的动力！数据源存放在我的资源下载区啦！

数据可视化（六）：Pandas爬取NBA球队排名、爬取历年中国人口数据、爬取中国大学排名、爬取sina股票数据、绘制精美函数图像

- 数据可视化（六）：Pandas爬取NBA球队排名、爬取历年中国人口数据、爬取中国大学排名、爬取sina股票数据、绘制精美函数图像
- - 1. 爬取NBA球队排名页面，并进行分析
  - 2. 爬取以下网址的历年中国人口数据进行并进行分析
  - 3. 获取大学排名数据并进行分析
  - 4. 获取sina股票数据并进行分析
  - 5. matplotlib模仿绘图
  - 6. matplotlib模仿绘图

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams["font.family"]=['SimHei']
plt.rcParams['axes.unicode_minus']=False

1. 爬取NBA球队排名页面，并进行分析

页面url https://nba.hupu.com/standings

提示：

data = pd.read_html(url, header=0) #header=0 去掉第一行列索引

# 爬取数据并将东部和西部联盟存放到df1 df2
url = "https://nba.hupu.com/standings"
data = pd.read_html(url,header=0) #header=0 去掉第一行列索引
data_merge = pd.concat([df,data[0]])

data_merge.columns = data_merge.iloc[0,:]
data_merge = data_merge.iloc[1:]

# 重置索引，不保留原索引作为新列  
data_merge.reset_index(drop=True, inplace=True)

# 东部数据
df1 = data_merge.iloc[0:15,:]
df1

# 西部数据
df2 = data_merge.iloc[17:,:]
df2.reset_index(drop=True, inplace=True)  
df2

# 将df1增加一列"所属联盟"，赋值为"东部赛区"
df1["所属联盟"] = "东部赛区"
df1

# 将df2增加一列"所属联盟"，赋值为"西部赛区"
df2["所属联盟"] = "西部赛区"
df2

# 将df1、df2合并成df
df_merge = pd.concat([df1,df2], axis = 0)
df_merge.reset_index(drop=True,inplace=True)
df_merge

# 将df数据保存为csv文件 nba.csv
df_merge.to_csv('./nba.csv', encoding='utf-8', index=False,sep=",")

# 将所有球队按照 胜率(百分比) 降序排序，排名相同的队伍按 失分 升序排名
# 提示：ascending也可以接收列表参数
df_merge.sort_values(by=["胜率","失分"],ascending=[False,True]).reset_index(drop=True)

# 对df按“所属联盟”分组，计算胜、负、胜率的最大值、最小值、均值、标准差
# 注意：百分比不是数值，要转换成小数
# 转换数值类型
df_merge["胜"] = df_merge["胜"].astype(int)
df_merge["负"] = df_merge["负"].astype(int)
# 将百分比字符串转换为小数  
df_merge['胜率'] = df_merge['胜率'].str.replace('%', '').astype(float) / 100
df_merge.head()

df_grouped = df_merge.groupby(by='所属联盟').agg(
    {  
    '胜': ['max', 'min', 'mean', 'std'],  
    '负': ['max', 'min', 'mean', 'std'],  
    '胜率': ['max', 'min', 'mean', 'std']  
})

# 柱状图显示东西赛区的胜率（百分比）均值
# 提取胜率均值列，并重置列名以简化后续操作  
df_grouped_win_rate_mean = df_grouped['胜率']['mean'].reset_index()  
df_grouped_win_rate_mean.columns = ['所属联盟', '胜率均值']  
df_grouped_win_rate_mean

# 将胜率均值转换为百分比  
df_grouped_win_rate_mean['胜率均值_百分比'] = df_grouped_win_rate_mean['胜率均值'] * 100  
df_grouped_win_rate_mean

# 绘制柱状图  
plt.figure(figsize=(10, 6))  # 设置图形大小  
bars = plt.bar(df_grouped_win_rate_mean['所属联盟'], df_grouped_win_rate_mean['胜率均值_百分比'])  
  
# 设置数据标签  
def format_percent(x):  
    return "{:.2%}".format(x / 100)  
  
# 添加百分比形式的数据标签  
for rect in bars:  
    height = rect.get_height()  
    plt.text(rect.get_x() + rect.get_width() / 2, height, format_percent(height),  
             ha='center', va='bottom')  

plt.xlabel('所属联盟')  # 设置x轴标签  
plt.ylabel('胜率均值')  # 设置y轴标签  
plt.title('东西赛区胜率均值比较')  # 设置图形标题  
plt.xticks(rotation=0)  # 设置x轴刻度标签的旋转角度为0  
plt.tight_layout()  # 调整布局  
plt.ylabel('胜率均值 (%)')  # 将y轴标签更改为百分比形式  
plt.show()  # 显示图形

2. 爬取以下网址的历年中国人口数据进行并进行分析

url = ‘https://population.gotohui.com/’

# 爬取数据并存放到df，并将df保存为population.csv
url = 'https://population.gotohui.com/'
data = pd.read_html(url,header=0) #header=0 去掉第一行列索引

df = data[0]
df.to_csv("./population.csv", encoding='utf-8', index=False,sep=",")

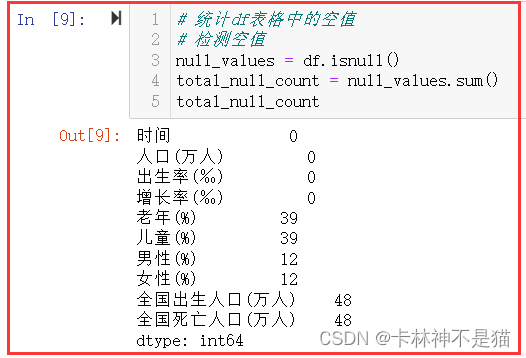
# 统计df表格中的空值
# 检测空值  
null_values = df.isnull() 
total_null_count = null_values.sum()  
total_null_count

在这里插入图片描述

# 将空值的列'老年人(%)'、'儿童(%)'中数据用前值替换；'男性(%)'、'女性(%)'用均值替换
# 使用前一个非空值替换 '老年人(%)' 和 '儿童(%)' 列中的空值  
df['老年(%)'].fillna(method='ffill', inplace=True)  
df['儿童(%)'].fillna(method='ffill', inplace=True)  

# 计算 '男性(%)' 和 '女性(%)' 列的均值，并替换这些列中的空值  
mean_male = df['男性(%)'].mean()  
mean_female = df['女性(%)'].mean()  
df['男性(%)'].fillna(mean_male, inplace=True)  
df['女性(%)'].fillna(mean_female, inplace=True) 
df

# 将除了 时间(年) 列外所有的列的数据改成保留小数点后2位小数
# 提示：采用lambda函数和applymap函数
# 保留除了'时间'字段之外的列的小数点后两位  
columns_to_round = ['人口(万人)', '出生率(‰)', '增长率(‰)', '老年(%)', '儿童(%)', '男性(%)', '女性(%)']  
  
df[columns_to_round] = df[columns_to_round].apply(lambda x: x.round(2))  
  
# 查看格式化后的输出，可以设置显示选项 （空值输出时浮点数格式）
pd.options.display.float_format = '{:.2f}'.format 

# 显示修改后的DataFrame  
df.head()

# 在同一张表上绘制历年人口出生率和增长率曲线
# 确保'时间'列是日期类型，这样可以按时间顺序绘制曲线  
df['时间'] = pd.to_datetime(df['时间'], format='%Y')  # 假设时间格式为'年'  
  
# 绘制出生率曲线  
plt.plot(df['时间'], df['出生率(‰)'], label='出生率(‰)', marker='o')  
  
# 绘制增长率曲线  
plt.plot(df['时间'], df['增长率(‰)'], label='增长率(‰)', marker='o', linestyle='--')  
  
# 设置图表标题和坐标轴标签  
plt.title('历年人口出生率和增长率曲线')  
plt.xlabel('时间')  
plt.ylabel('比率')  
  
# 显示图例  
plt.legend()  
  
# 显示网格  
plt.grid(True)  
  
# 格式化x轴以显示年份  
plt.gcf().autofmt_xdate()  
  
# 显示图表  
plt.show()

# 绘制男女比率差绝对值的曲线图
# 计算男女比率差的绝对值  
df['比率差绝对值'] = abs(df['男性(%)'] - df['女性(%)'])  
df

# 绘制男女比率差绝对值的曲线图  
plt.plot(df['时间'], df['比率差绝对值'], marker='o')  
  
# 设置图表标题和坐标轴标签  
plt.title('男女比率差绝对值曲线图')  
plt.xlabel('时间')  
plt.ylabel('比率差绝对值')  
  
# 显示网格  
plt.grid(True)    
  
# 显示图表  
plt.show()

# 在一个画布的四个子画布上(两行两列)分别画出：
# 1、近十年老人、儿童、其它（100减去老人、儿童占比）人群比率均值的柱状比较图
# 2、近五年男性、女性比率的柱状比较图
# 3、近十年人口增增长率和出生率的水平柱状图
# 4、2022年老人、儿童、其它的饼图

import matplotlib.pyplot as plt  
import pandas as pd  
  
# 假设df_1, df_2, df_3, df_4已经定义好，并且包含了需要绘制的数据  
  
# 创建一个2x2的画布和子图  
fig, axs = plt.subplots(2, 2, figsize=(12, 8))  
  
# 第一幅图：近十年老人、儿童、其它人群比率均值的柱状比较图  
bars = axs[0, 0].bar(df_1.columns, df_1.iloc[0])  
bar_width = 0.35  
axs[0, 0].set_title('近十年老人、儿童、其它人群比率均值的柱状比较图')  
axs[0, 0].set_xlabel('人群')  
axs[0, 0].set_ylabel('比率均值(%)')  
for bar in bars:  
    height = bar.get_height()  
    axs[0, 0].text(bar.get_x() + bar_width / 2, height, '{:.2f}'.format(height), ha='center', va='bottom')  
  
 # 第二幅图：近五年男性和女性比例的柱状比较图  
df_2 = df_2.sort_values(by='时间')  
bar_width = 0.35  
index_male = range(len(df_2))  
index_female = [i + bar_width for i in index_male]  
  
axs[0, 1].bar(index_male, df_2['男性(%)'], bar_width, label='男性比例')  
axs[0, 1].bar(index_female, df_2['女性(%)'], bar_width, label='女性比例')  
  
# 设置x轴的标签位置为index_male的中间位置，并且标签内容为df_2['时间']的值  
tick_positions = [i + bar_width / 2 for i in index_male]  
axs[0, 1].set_xticks(tick_positions)  
axs[0, 1].set_xticklabels(df_2['时间'])  # 设置x轴的标签内容  
  
# 设置x轴刻度标签的旋转角度  
axs[0, 1].tick_params(axis='x', rotation=45)  # 旋转x轴刻度标签  
  
axs[0, 1].set_title('近五年男性和女性比例的柱状比较图')  
axs[0, 1].set_xlabel('年份')  
axs[0, 1].set_ylabel('比例(%)')  
axs[0, 1].legend()  
  
# 第三幅图：近十年人口增长率和出生率水平柱状图  
axs[1, 0].barh(df_3['时间'], df_3['增长率(‰)'], label='增长率', color='skyblue')  
axs[1, 0].barh(df_3['时间'], df_3['出生率(‰)'], left=df_3['增长率(‰)'], label='出生率', color='lightcoral')  
axs[1, 0].set_title('近十年人口增长率和出生率水平柱状图')  
axs[1, 0].set_xlabel('千分比')  
axs[1, 0].set_ylabel('年份')  
axs[1, 0].legend()  
axs[1, 0].grid(axis='x', alpha=0.75)  
  
# 第四幅图：2022年老人、儿童、其他人群分布的饼图  
labels = df_4.columns  
sizes = df_4.iloc[0]  
axs[1, 1].pie(sizes, labels=labels, autopct='%1.1f%%', startangle=90)  
axs[1, 1].axis('equal')  
axs[1, 1].set_title('2022年老人、儿童、其他人群分布')  
  
# 调整子图间距  
plt.tight_layout()  
  
# 显示整个画布  
plt.show()

# 在同一幅图上画出'出生率(‰)', '增长率(‰)'箱线图。
import seaborn as sns  
import matplotlib.pyplot as plt  
  
# 设置图形大小  
plt.figure(figsize=(10, 6))  
  
# 绘制箱线图  
sns.boxplot(data=df[['出生率(‰)', '增长率(‰)']])  
 
# 设置标题和轴标签  
plt.title('出生率和增长率的箱线图')  
plt.xlabel('指标')  
plt.ylabel('值 (‰)')  
  
# 显示图形  
plt.show()

# 利用散点图寻找 ‘增长率(‰)’ 异常值的年份，即寻找增长率背离正常变化范围的年份。
import matplotlib.pyplot as plt  
import pandas as pd  
import numpy as np  
  
# 计算增长率的四分位数  
Q1 = df_6['增长率(‰)'].quantile(0.25)  
Q3 = df_6['增长率(‰)'].quantile(0.75)  

  
# 定义正常值范围，这里使用0.8倍IQR作为异常值的界限  
lower_bound = Q1 - 0.8 * IQR  
upper_bound = Q3 + 0.8 * IQR  
  
# 识别异常值  
outliers = df_6[(df_6['增长率(‰)'] < lower_bound) | (df_6['增长率(‰)'] > upper_bound)]  
  
# 绘制散点图  
plt.figure(figsize=(10, 6))  
plt.scatter(df_6['时间'], df_6['增长率(‰)'], color='blue', label='正常值')  
  
# 在图上标注异常值  
plt.scatter(outliers['时间'], outliers['增长率(‰)'], color='red', label='异常值')  
for index, row in outliers.iterrows():  
    plt.annotate(f'({row["时间"]}, {row["增长率(‰)"]})', (row['时间'], row['增长率(‰)']))  

# 设置标题和轴标签  
plt.title('增长率随时间变化的散点图及异常值标注')  
plt.xlabel('时间')  
plt.ylabel('增长率(‰)')  
  
# 显示图例  
plt.legend()  
  
# 显示网格线  
plt.grid(True)  
  
# 显示图形  
plt.show()

# 利用正态分布方法（类似3𝜎方法，采用1.5𝜎）找出增长率异常值
import pandas as pd  
import numpy as np  
import matplotlib.pyplot as plt  
  
# 计算增长率的均值和标准差  
mean_growth_rate = df_7['增长率(‰)'].mean()  
std_growth_rate = df_7['增长率(‰)'].std()  
  
# 设定异常值的阈值，这里使用1.5倍标准差  
threshold = mean_growth_rate + 1.5 * std_growth_rate  
# 对于低于均值的异常值，使用负的1.5倍标准差  
lower_threshold = mean_growth_rate - 1.5 * std_growth_rate  
  
# 识别异常值  
outliers_upper = df_7[df_7['增长率(‰)'] > threshold]  
outliers_lower = df_7[df_7['增长率(‰)'] < lower_threshold]  
outliers = pd.concat([outliers_upper, outliers_lower])  
  
# 绘制散点图，并标注异常值  
plt.figure(figsize=(10, 6))  
plt.scatter(df_7['时间'], df_7['增长率(‰)'], color='blue', label='正常值')  
  
# 标注异常值  
plt.scatter(outliers['时间'], outliers['增长率(‰)'], color='red', label='异常值')  
for index, row in outliers.iterrows():  
    plt.annotate(f'({row["时间"]}, {row["增长率(‰)"]})', (row['时间'], row['增长率(‰)']))  

# 设置标题和轴标签  
plt.title('增长率随时间变化的散点图及异常值标注')  
plt.xlabel('时间')  
plt.ylabel('增长率(‰)')  
  
# 显示图例  
plt.legend()  
  
# 显示网格线  
plt.grid(True)  
  
# 显示图形  
plt.show()

3. 获取大学排名数据并进行分析

获取数据地址：http://www.jdxzz.com/paiming/2022/0830/9651208.html
数据爬取后，存在“主榜”和“副榜”，只保留主榜数据

提示：

data = pd.read_html(url, header=0) #header=0 去掉第一行列索引
df = pd.DataFrame(data[0]) # 只获取主榜表格数据

# 获取“主榜”数据并放入df
# 将数据保存到universities.csv
url = 'http://www.jdxzz.com/paiming/2022/0830/9651208.html'
data = pd.read_html(url,header=0) #header=0 去掉第一行列索引
data

df = data[0]
df.to_csv("../data/universities.csv", encoding='utf-8', index=False,sep=",")

# 不同 办学层次 的大学数量？
# 画出不同 办学层次 的大学数量的折线图，按升序画
df_group = df.groupby(by='办学层次')["办学层次"].count().reset_index(name='数量')
df_group = df_group.sort_values(by='数量',ascending=True).reset_index(drop=True)
df_group

import matplotlib.pyplot as plt  
  
# 绘制折线图  
plt.figure(figsize=(10, 6))  # 设置图形大小  
plt.plot(df_group['办学层次'], df_group['数量'], marker='o')  # 绘制折线，并使用圆圈标记数据点  
  
# 设置标题和轴标签  
plt.title('不同办学层次的大学数量折线图')  
plt.xlabel('办学层次')  
plt.ylabel('数量')  
  
# 显示网格线  
plt.grid(True)  
  
# 显示图形  
plt.show()

# 显示只包含 财经大学、财经学院 的子表，并按排名排列
# 提示：Pandas 中类似SQL中的like查询
# df.query('column.str.contains("string")', engine='python')

df_gdufe = df.query('学校名称.str.contains("财经")', engine='python').reset_index(drop=True)
df_gdufe

# 计算不同 办学层次 大学的 总分均值、排名均值，四舍五入取一位小数
df_grouped = df.groupby(by='办学层次').agg(
    {  
    '总分': 'mean',  
    '全国排名': 'mean'  
}).round(1)

df_grouped.columns = ["总分均值","排名均值"]
df_grouped

4. 获取sina股票数据并进行分析

获取数据地址：http://vip.stock.finance.sina.com.cn/q/go.php/vComStockHold/kind/jjzc/index.phtml?p=
数据分6页，p=1代表第1页

提示

df = pd.DataFrame()
for i in range(6):    
    url = 'http://vip.stock.finance.sina.com.cn/q/go.php/vComStockHold/kind/jjzc/index.phtml?p={page}'.format(page=i+1)
    df = pd.concat([df, pd.read_html(url)[0]]) # 按行连接
    print("第{page}页爬取成功！".format(page=i+1))

# 爬取6页表格数据并合并数据到df，再保存到sina.csv文件
df.to_csv('../data/sina.csv', encoding='utf-8', index=False,sep=",")

# 从sina.csv中读取到df，并随机显示10行数据
df = pd.read_csv(fr"../data/sina.csv",encoding='utf-8', sep=",")
df.sample(10)

# 基金持股比例最高的10个股份的 代码 简称 比例
df_top = df.sort_values(by="持股比例(%)",ascending=False).reset_index(drop=True)[["代码","简称","持股比例(%)"]]
df_top.head(10)

# 按照持股家数分组 计算 持股占已流通A股比例(%) 的平均数 降序
df.groupby(by="家数")[["持股占已流通A股比例(%)"]].mean().sort_values(by="持股占已流通A股比例(%)",ascending=False)

# 统计银行的平均 家数 和 平均 持股比例(%) （简称含有银行字眼）
df_bank = df.query('简称.str.contains("银行")', engine='python').reset_index(drop=True)[["简称","家数","持股比例(%)"]]
df_bank

# 统计家数增加最多的10个股票，按 持股占已流通A股比例(%) 降序排序
df["增加家数"] = df["家数"] - df["上期家数"]
df.head()

df_10 = df.sort_values(by="增加家数",ascending=False).reset_index(drop=True).head(10)
df_10

df_10.sort_values(by="持股占已流通A股比例(%)",ascending=False).reset_index(drop=True)

# 将 持股占已流通A股比例(%)>8 同时 持股比例(%)>5 的股票挑选出来
df.loc[(df["持股占已流通A股比例(%)"] > 8) & (df["持股比例(%)"] > 5)]

# 将%号加到 持股占已流通A股比例(%) 和 持股比例(%) 两列， 元素值改为字符串
# 使用apply和lambda表达式添加%号，并转换为字符串  
df['持股占已流通A股比例(%)'] = df['持股占已流通A股比例(%)'].apply(lambda x: f"{x}%" if not pd.isna(x) else pd.NA)  
df['持股比例(%)'] = df['持股比例(%)'].apply(lambda x: f"{x}%" if not pd.isna(x) else pd.NA)  
  
# 查看修改后的DataFrame  
df

5. matplotlib模仿绘图

按绘图样式，写出绘制代码。

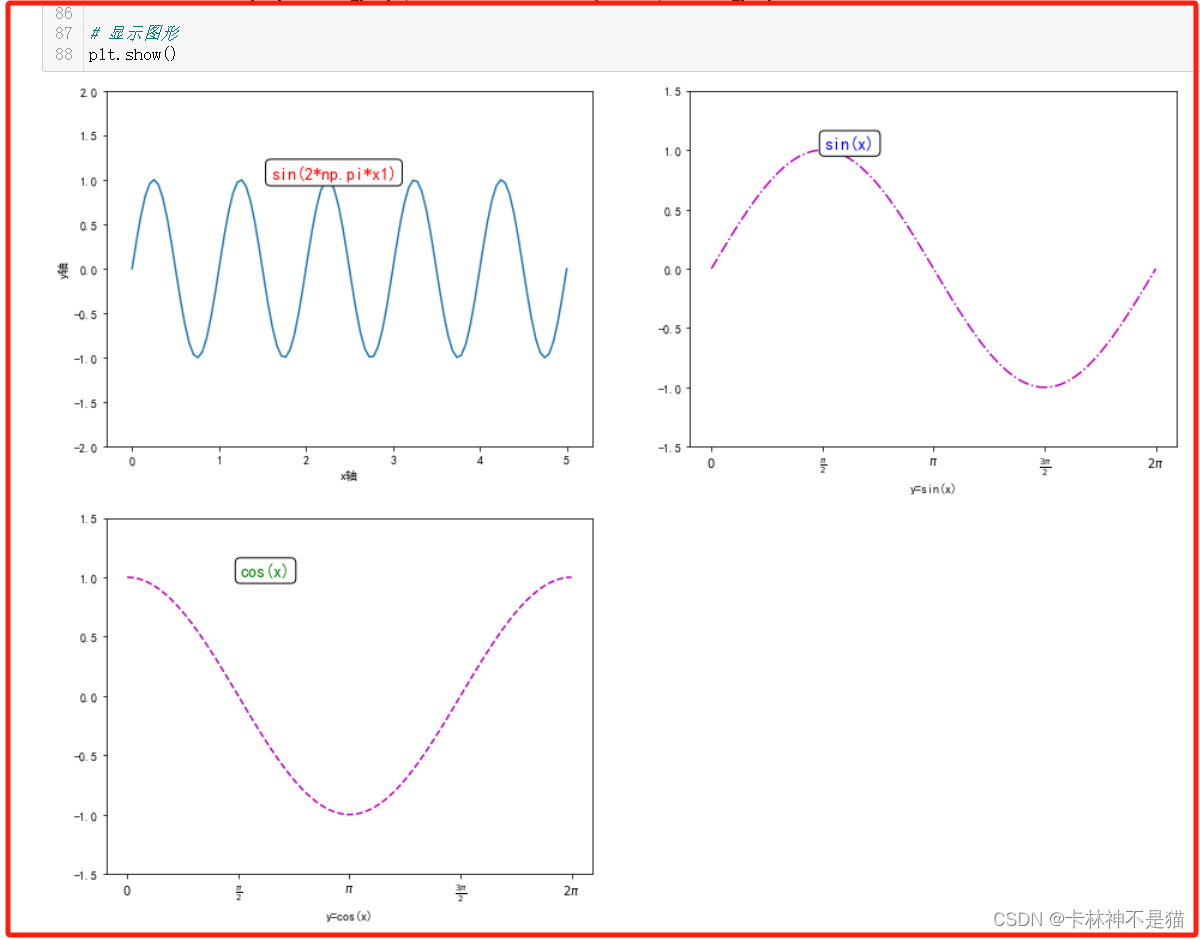
在这里插入图片描述

# 代码
# 创建⼀些数据
x1 = np.linspace(0, 5, 100)
x2 = np.linspace(0, 2*np.pi, 100)
x3 = np.linspace(0, 2*np.pi, 100)

y1 = np.sin(2*np.pi*x1)
y2 = np.sin(x2)
y3 = np.cos(x3)
# 创建⼀个新的Figure,包含2x2个Axes
fig = plt.figure(figsize=(16, 12))
# 在2x2⽹格中创建4个Axes

# =========================================第一幅图=========================================
plt.subplot(2, 2, 1) # 第⼀⾏第⼀个
plt.plot(x1, y1, linestyle='-')
# 设置左上角的子图横坐标范围为0到5（留白效果），纵坐标范围为-2.0到2.0  
plt.xlim(-0.3, 5.3)  
plt.ylim(-2.0, 2.0)  
plt.xlabel("x轴")
plt.ylabel("y轴")

# =========================================第二幅图=========================================
plt.subplot(2, 2, 2) # 第⼀⾏第⼆个
plt.plot(x2, y2, linestyle='-.',color='m')
# 设置横坐标的刻度位置和标签  
ticks = np.arange(0, 2 * np.pi + np.pi/4, np.pi/2)  # 刻度位置：从0开始，每隔π/2一个刻度  
labels = [r'$0$', r'$\frac{\pi}{2}$', r'$\pi$', r'$\frac{3\pi}{2}$', r'$2\pi$']  # 对应的标签  
plt.xticks(ticks, labels)  # 设置刻度和标签  
  
# 设置横坐标范围，稍微扩大以留下空白  
plt.xlim(-0.3, 2 * np.pi + 0.3)  
plt.ylim(-1.5, 1.5) 
plt.xlabel("y=sin(x)")

# =========================================第三幅图=========================================
plt.subplot(2, 2, 3) # 第⼆⾏第⼀个
plt.plot(x3, y3, linestyle='--',color='m')
# 设置横坐标的刻度位置和标签  
ticks = np.arange(0, 2 * np.pi + np.pi/4, np.pi/2)  # 刻度位置：从0开始，每隔π/2一个刻度  
labels = [r'$0$', r'$\frac{\pi}{2}$', r'$\pi$', r'$\frac{3\pi}{2}$', r'$2\pi$']  # 对应的标签  
plt.xticks(ticks, labels)  # 设置刻度和标签  
  
# 设置横坐标范围，稍微扩大以留下空白  
plt.xlim(-0.3, 2 * np.pi + 0.3)  
plt.ylim(-1.5, 1.5)  
plt.xlabel("y=cos(x)")

plt.show()

6. matplotlib模仿绘图

按绘图样式，写出绘制代码。

绘图函数：y=sin(x), y=cos(x), x = np.linspace(-np.pi, np.pi, 256, endpoint=True)
绘制填充区域: 紫色区域：(-2.5<x)&(x<-0.5)，绿色区域：sinx>0.5

在这里插入图片描述

# 代码
import numpy as np
import matplotlib.pyplot as plt

# 创建一个大小为(10, 6)的图像，设置分辨率为80
plt.figure(figsize=(10,6), dpi=80)

# 生成一个从-pi到pi的256个点的等差数列
x = np.linspace(-np.pi, np.pi, 256, endpoint=True)

# 计算x对应的sin和cos值
C, S = np.cos(x), np.sin(x)

# 绘制sin(x)曲线，设置颜色为蓝色，线宽为2.5，线型为实线
plt.plot(x, S, color="blue", linewidth=2.5, linestyle="-", label=r'$sin(x)$')

# 绘制cos(x)曲线，设置颜色为红色，线宽为2.5，线型为实线
plt.plot(x, C, color="red", linewidth=2.5, linestyle="-", label=r'$cos(x)$')

# 填充cos(x)曲线在x范围(-2.5, -0.5)之间的区域，颜色为深紫色(DarkViolet)，透明度为0.5
plt.fill_between(x, C, where=((-2.5 < x) & (x < -0.5)), color='DarkViolet', alpha=0.5)

# 填充sin(x)曲线在值大于0.5的区域，颜色为深绿色(DarkGreen)，透明度为0.5
plt.fill_between(x, S, where=(S > 0.5), color='DarkGreen', alpha=0.5)

# 添加图例，位于左上角，并设置图例的背景色为白色
plt.legend(loc='upper left', facecolor='white')

# 设置x轴和y轴的范围
plt.xlim(x.min()*1.2, x.max()*1.2)
plt.ylim(C.min()*1.2, C.max()*1.2)

# 设置x轴和y轴的刻度标签
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi], [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])
plt.yticks([-1,1], [r'$-1$', r'$1$'])

# 移动坐标轴到原点
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['bottom'].set_position(('data',0))
ax.spines['left'].set_position(('data',0))

# 设置特殊点的标记和注释
t = 2*np.pi/3
plt.plot([t,t],[0,np.cos(t)], color ='red', linewidth=2.5, linestyle="--")
plt.scatter([t,],[np.cos(t),], 50, color ='red')
plt.annotate(r'$sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$',
             xy=(t, np.sin(t)), xycoords='data',
             xytext=(+10, +30), textcoords='offset points', fontsize=16,
             arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))

plt.plot([t,t],[0,np.sin(t)], color ='blue', linewidth=2.5, linestyle="--")
plt.scatter([t,],[np.sin(t),], 50, color ='blue')
plt.annotate(r'$cos(\frac{2\pi}{3})=-\frac{1}{2}$',
             xy=(t, np.cos(t)), xycoords='data',
             xytext=(-90, -50), textcoords='offset points', fontsize=16,
             arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))

# 添加标题，并设置标题的颜色为绿色，位置为中心
plt.title('绘图实例之SIN()&COS()', color="green", loc="center")

# 添加网格线
plt.grid(True)

# 显示图像
plt.show()