目录
DFS:剪枝
DFS:有哪些剪枝方法
DFS例题一:剪格子
【思路】
DFS例题二:路径之谜
【样例分析】
DFS例题三:四阶幻方
【思路】
【做法一】
【做法二】
DFS例题三:分考场
【样例分析】
【思路】
DFS习题
DFS:剪枝
剪枝:把不会产生答案的或不必要的枝条“剪掉”。
剪枝的关键:剪什么枝、在哪里减。
剪枝是搜索常用的优化手段,常常能把指数级的复杂度,优化到近似多项式的复杂度。
DFS:有哪些剪枝方法
- 可行性剪枝:对当前状态进行检查,如果当前条件不合法就不再继续,直接返回。
- 搜索顺序剪枝:搜索树有多个层次和分支,不同的搜索顺序会产生不同的搜索树形态。
- 最优性剪枝:在最优化问题的搜索过程中,如果当前花费的代价已超过前面搜索到的最优解,那么本次搜索已经没有继续进行下去的意义,停止对当前分支的搜索。
- 排除等效冗余:搜索的不同分支,最后的结果是一样的,那么只搜一个分支就够了。
- 记忆化搜索:在递归的过程中,有许多分支被反复计算,会大大降低算法的执行效率。将已经计算出来的结果保存起来,以后需要用到的时候直接取出结果,避免重复运算,从而提高了算法的效率。
DFS例题一:剪格子
剪格子lanqiao0J题号211
【题目描述】
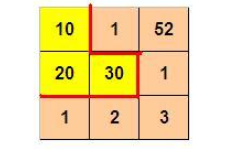
如下图所示,3 x 3 的格子中填写了一些整数。
我们沿着图中的红色线剪开,得到两个部分,每个部分的数字和都是 60。
本题的要求就是请你编程判定:对给定的 m×n 的格子中的整数,是否可以分割为两个部分,使得这两个区域的数字和相等。
如果存在多种解答,请输出包含左上角格子的那个区域包含的格子的最小数目。
如果无法分割,则输出 0。
【输入描述】
程序先读入两个整数 m,n 用空格分割 (m,n<10),表示表格的宽度和高度。
接下来是 n 行,每行 m 个正整数,用空格分开。每个整数不大于 10^4。
【输出描述】
在所有解中,包含左上角的分割区可能包含的最小的格子数目。
【输入输出样例】
输入
3 3 10 1 52 20 30 1 1 2 3输出
3
【思路】
一道极典型的DFS题
做法:先求所有格子的和sum,然后用DFS找一个联通区域,看这个区域的和是否为sum/2。
剪枝:如果DFS到的部分区域的和已经超过sum/2,就不用继续DFS了。
这种格子DFS搜索题,是蓝桥杯的常见考题。
def dfs(x,y,c,s): # x,y是坐标点,c是格子数,s是求得的和
global sum_num,ans
if 2*s > sum_num: return # 剪枝:当前s超过sum的一半就不需要继续
if 2*s == sum_num: # 终止条件:当前s刚好是总面积的一半
if ans>c and vis[0][0]== 1: ans = c # 格子数更小且访问过左上角,保留该格子数
return
vis[x][y] = 1 # 保存现场:标记为访问过
# 下面代码是对格子进行遍历
dir = [(1,0),(-1,0),(0,-1),(0,1)] # 四个方向
for u, v in dir: # 在当前坐标往4个方向走
tx,ty = x+u,y+v
# 上面两行还可以这样写
#for u in range(4):
# tx,ty = x+dir[u][0],y+dir[u][1]
if 0 <= tx <= n-1 and 0 <= ty <= m - 1: # 不能出界
if vis[tx][ty] == 0: # 没有访问过
dfs(tx,ty, c+1, s+a[x][y]) # 访问下一个点
vis[x][y] = 0 # 恢复现场
m, n = map (int,input ().split()) # 格子的宽和高(n行m列)
a = [list (map(int,input ().split())) for _ in range(n)] # 存格子:每次读一行
vis = [[0]*m for _ in range(n)] # 记录访问情况
sum_num = 0
for i in a:
sum_num += sum(i) # 对a求和 sum(i):第i行的和
ans = 1000000 # ans是最小格子数,初始化为无穷大
dfs (0,0,0,0) # 搜索最少格子数
print(ans)DFS例题二:路径之谜
路径之谜2016年第七届决赛,lanqiao0J题号89
【题目描述】
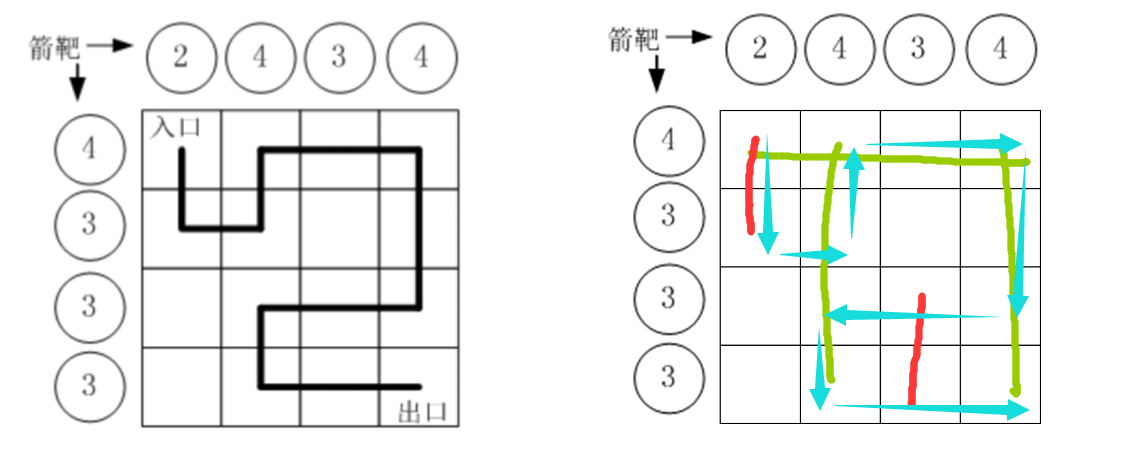
小明冒充 XX 星球的骑士,进入了一个奇怪的城堡。城堡里边什么都没有,只有方形石头铺成的地面。假设城堡地面是 n×n 个方格。如下图所示。
按习俗,骑士要从西北角走到东南角。可以横向或纵向移动,但不能斜着走,也不能跳跃。每走到一个新方格,就要向正北方和正西方各射一箭。(城堡的西墙和北墙内各有 n 个靶子)同一个方格只允许经过一次。但不必走完所有的方格。如果只给出靶子上箭的数目,你能推断出骑士的行走路线吗?有时是可以的,比如上图中的例子。
本题的要求就是已知箭靶数字,求骑士的行走路径(测试数据保证路径唯一)
【输入描述】
第一行一个整数 N (0≤N≤20),表示地面有 N×N 个方格。
第二行 N 个整数,空格分开,表示北边的箭靶上的数字(自西向东)
第三行 N 个整数,空格分开,表示西边的箭靶上的数字(自北向南)
【输出描述】
输出一行若干个整数,表示骑士路径。
为了方便表示,我们约定每个小格子用一个数字代表,从西北角开始编号: 0,1,2,3 ⋯
比如,上图中的方块编号为:
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
输入输出样例
输入
4 2 4 3 4 4 3 3 3输出
0 4 5 1 2 3 7 11 10 9 13 14 15
【样例分析】
首先可以把靶子上四支箭的位置先确定下来(用绿色标记),然后再确定其他靶子所在的行和列的位置,发现第一行的两支箭已经确定了一支,而另一只箭只能出现在点4(用红色标记),若出现在点8或点12则没办法走到东南角。那么剩下的箭的位置也确定了(用红色标记)。
- DFS:题目要求输出一条路径,用DFS很合适,DFS搜索过程中,自然生成一条路径。
- 剪枝:每走到一个格子,对应的靶子上箭多一支,靶子上的箭等于给定的数字后,就不用再DFS下去了。(或者做减法,靶子的数字减到0)
- 记录路径的技巧:根据题目的要求,用栈来跟踪DFS的过程,记录DFS走过的路径,是最方便的。DFS到某个格子时,把这个格子放到栈里,表示路径增加了这个格子。DFS回溯的时候,退出了这个格子,表示路径上不再包括这个格子,需要从栈中弹走这个格子。
def dfs(x, y):
if a[x]<0 or b[y]<0: return # 剪枝:有靶子上的箭数<0
if x==n-1 and y==n-1: # 终止条件:到达终点
ok=1
for i in range(n) : # 到达终点但箭数对不上,排除
if a[i]!=0 or b[i]!=0: ok=0 ; return
if ok==1 : # # 到达终点且箭数对上,把path的路径打印出来
if a[i]!=0 or b[i]!=0: ok=0 ; return
for i in range(len(path)) : print(path[i], end=' ')
# 遍历每一点
for d in [(1,0),(-1,0),(0,1),(0,-1)]:
tx = x+d[0]; ty = y+d[1]
if 0<= tx < n and 0<= ty < n and vis[tx][ty] == 0: # 没有越界且没有访问过
# 下面三行是保护现场
vis[tx][ty] = 1
path. append(tx*n + ty) # 进栈,记录路径。tx*n + ty:该点的编号
a[tx] -= 1; b[ty] -= 1 # 经过这个点,这个点的行和列的箭数-1
# 搜索下一个
dfs (tx,ty)
# 下面三行是恢复现场
path. pop () # 出栈,DFS回溯
a[tx] += 1 ; b[ty] += 1
vis[tx][ty] = 0
n = int (input())
vis = [[0]*n for i in range(n)] # 记录访问情况
b = list (map(int,input ().split())) # 北边靶子上箭数
a = list (map(int,input ().split())) # 西边靶子上箭数
path = [0] # 用栈记录路径,初始化一个0,因为从编号0(西北角)开始的
vis[0][0]=1 # 从左上角出发,标记为已访问
a[0] -= 1; b[0] -= 1 # 经过该点对应方位上的箭-1
dfs (0,0) # 从坐标点(0,0)开始搜索DFS例题三:四阶幻方
四阶幻方2015年第六届决赛,lanqiao0J题号689
【题目描述】
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
把 1 ~ 16 的数字填入 4×4 的方格中,使得行、列以及两个对角线的和都相等,满足这样的特征时称为:四阶幻方。
四阶幻方可能有很多方案。如果固定左上角为 1,请计算一共有多少种方案。
比如:
1 2 15 16 12 14 3 5 13 7 10 4 8 11 6 9以及:
1 12 13 8 2 14 7 11 15 3 10 6 16 5 4 9就可以算为两种不同的方案。
【思路】
暴力解决:除了1,循环遍历数字2~16,有15!=1.3×10^12种排列,但时间太久,无法把所有排列都试一遍。
剪枝:每种排列,只要前面一些数字不适合,就不用再计算下去了。(类似于“暑假作业”的剪枝)
【做法一】
正常剪枝:按顺序来剪枝,先搜索到第4个,剪枝第一行(浅蓝色),搜索到第8个和第12个,分别剪枝第二行和第三行(浅蓝色),搜索到第13个,剪枝第一列和一条对角线(红色)。搜索到第13和第14个,分别剪枝第二列和第三列(绿色)。搜索到16个时,再判断最后一行和最后一列和一条对角线(深蓝色),如果满足要求,ans+1。

def dfs(n):
global ans
if n>=4 and a[0]+a[1]+a[2]+a[3]!=34: #各种剪枝情况
return
if n>=8 and a[4]+a[5]+a[6]+a[7]!=34:
return
if n>=12 and a[8]+a[9]+a[10]+a[11]!=34:
return
if n>=13 and (a[3]+a[6]+a[9]+a[12]!=34 or a[0]+a[4]+a[8]+a[12]!=34):
return
if n>=14 and a[1]+a[5]+a[9]+a[13]!=34:
return
if n>=15 and a[2]+a[6]+a[10]+a[14]!=34:
return
if n>=16 and (a[12]+a[13]+a[14]+a[15]!=34 or a[0]+a[5]+a[10]+a[15]!=34 or a[3] + a[7] + a[11] + a[15]!= 34):
return
if n==16: #到达最后,且符合条件
ans+=1
for i in range(2,17): #分别排列2-16这些数
if vis[i]==0:
a[n]=i
vis[i]=1
dfs(n+1)
vis[i]=0
ans=0
a=[0]*17
vis=[0]*17
a[0]=1 #固定a[0]是1
vis[1]=1
dfs(1)
print(ans)
#print(416)运行时间:2min,有点久!
【做法二】
尽快剪枝可以减少运行时间!
0-15的编号不一定要按顺序来排,因为每个位置都需要遍历2~16这些数,每个位置其实是一样的,所以可以按照最快剪枝的方式来编号。 下面这个方式在n小于12的情况下剪枝4次,而按顺序来排的情况只剪枝2次。
比如说搜索到7这个位置,我就可以判断第一列了 。
如果按照原来0-15的顺序来编,要搜到m[13]才能判断第一列的情况
def dfs(n):
global cnt
# 剪枝
if n >= 4 and m[0] + m[1] + m[2] + m[3] != 34: return # 第一行
if n >= 7 and m[0] + m[4] + m[5] + m[6] != 34: return # 第一列
if n >= 10 and m[1] + m[7] + m[8] + m[9] != 34: return # 第二列
if n >= 11 and m[3] + m[6] + m[8] + m[10] != 34: return # 对角线
if n >= 12 and m[4] + m[7] + m[10] + m[11] != 34: return # 第二行
if n >= 14 and m[5] + m[8] + m[12] + m[13] != 34: return # 第三行
if n >= 15 and m[2] + m[10] + m[12] + m[14] != 34: return # 第三列
if n == 16 and (m[6] + m[9] + m[14] + m[15] != 34 # 最后一行/最后一列/对角线
or m[3] + m[11] + m[13] + m[15] != 34
or m[0] + m[7] + m[12] + m[15] != 34) :return
if n == 16: cnt += 1
# 对每个位置用2~16去遍历
for i in range(2,17): #2~16的全排列
if vis[i] == 0:
m[n]=i
vis[i] = 1 # 保护现场
dfs(n + 1)
vis[i] = 0 # 恢复现场
cnt = 0
m = [0]*17 # 一维数组表示幻方
m[0] = 1 # 1被固定
vis = [0]*17
vis[1] = 1
dfs(1) # 从1开始搜索
print(cnt)运行时间:2s
DFS例题三:分考场
分考场2017年第八届决赛,lanqiaoo题号109
【题目描述】
n 个人参加某项特殊考试。
为了公平,要求任何两个认识的人不能分在同一个考场。
求是少需要分几个考场才能满足条件。
【输出描述】
输入格式:
第一行,一个整数 n (1≤n≤100),表示参加考试的人数。
第二行,一个整数 m,表示接下来有 m 行数据。
以下 m 行每行的格式为:两个整数 a,b,用空格分开 (1≤a,b≤n )表示第 a 个人与第 b 个人认识。
【输出描述】
输出一行一个整数,表示最少分几个考场。
【输入输出样例】
输入
5 8 1 2 1 3 1 4 2 3 2 4 2 5 3 4 4 5输出
4
【样例分析】
五个人 前三个关系1 2,1 3,1 4说明1不能和234同一个考场,至少两个考场;关系2 3和2 4说明2和3 4不能同一个考场,至少三个考场。关系3 4说明3和4不能一个考场,至少四个考场,剩下的关系2 5和4 5说明5不能和2 4同考场,可以和1 3同考场,所以需要四个考场。
【思路】
- 从第1个考场开始,逐个加入考生。每新加进来一个人x,都与已经开设的考场里面的人进行对比,如果认识,就换个考场。直到找到一个考场,考场里面所有的人都不认识x,x就可以坐在这里。如果所有已经开设的考场都有熟人,就开一个新考场给x坐。
- 这个模拟的结果是得到了一个可行的考场安排,但这个安排的考场数量不一定是最少的。
- 题目求最少考场数量,需要把所有可能的考场安排都暴力地试一遍,找到最少的那个考场安排。
用DFS来暴力搜索:
- 用DFS搜索所有可能的情况,得到最少考场。暴力搜索所有的考场安排,计算量很大
- 剪枝:用剪枝来减少搜索。在搜索一种新的可能的考场安排时,如果需要的考场数量已经超过了原来某个可行的考场安排,就停止(最优性剪枝)。
def dfs (x, room) :
global num, p
if room > num : return # 剪枝:需要的考场数量已经错过了原来某个可行的考场安排,停止
if x > n : # 终止条件:人数超过了
if room< num : num = room # 当前考场数小于最佳考场数,更新最佳考场数
return
# 1~room考场能坐
for j in range(1, room+1):
k = 0
while p[j][k] and a[x][p[j][k]] == 0: # 若该考场有人且两人不认识
k += 1 # 可以在该考场,座位号每次+1,直到找到没有人的座位。
if p[j][k] == 0 : # k座位没人坐
p[j][k] = x # 保护现场:第j考场的k座位,安排x坐
dfs(x+1 , room) # 安排下一人
p[j][k]= 0 # 恢复现场:回溯,放开这个位置
# 1~room考场都不能坐
p[room+1][0] = x # x只能坐第room+1个考场的第一个位置
dfs (x+1 , room+1) # 继续安排第x+1人,试试第1~第room+1考场
p[room+1][0] = 0 # 回溯
n = int (input ())
m = int (input())
num = 110
p = [[0 for i in range(n+1)]for j in range(n+1)] # 二维数组存考场:第一维:考场号、第二维:座位号
a = [[0 for i in range(n+1)]for j in range(n+1)] # 二维数组存关系
for i in range (m) :
u, v = map(int, input ().split())
a[u][v] = a[v][u] = 1 # 将两人的关系存入a
dfs(1,0) # 从第一个人开始搜索
print (num)DFS习题
https://www.lanqiao.cn/problems/题号/learning/
大家只需要将下面题号补充在上面链接的题号就能找到这一题
青蛙跳杯子102,发现环108,合根植物110,填字母游戏113,机器人塔118,四平方和122,取球博弈123,卡片换位125、生命之树131,穿越雷区141、长草149、小朋友崇拜圈182,剪格子211,版本分支223,迷宫与陷阱229,调手表230,分考场237,最长子序列244,九宫重排261,网络寻路263,危险系数264,约数倍数选卡片265,字母阵列621,魔方状态643,算式649,凑平方数653,方格填数664,完美正方形685,五星填数687,生成回文数691,走迷宫1216,N皇后问题1508,最少操作数1509。