Day1
微积分之屠龙宝刀(武林秘籍)
之前的一些东西都在pdf上记得笔记, 没有在这个上面展示一遍,只好学到相关内容的时候再提叙啦;所以其实再写这个小记的时候,我已经看了一半的书,但是不要紧,前面大多比较简单;
学习方法就是:emmm ipad 上面看书加计算;然后 笔记本上进行讲解(有一些公式太麻烦,就直接粘贴了嘿嘿)
不做流水线的鸭子,做农村下笨鸡蛋的鸡
17 隐微分法
需要的知识chain rule 基本的求导法则
微分可以分为两种显示的不必多说, 隐式的是因为 我们有时候没办法将y 单独表示,例如:
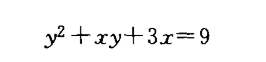
这个时候想求 d x d y \frac{dx}{dy} dydx 就 把y当成x的函数, 然后利用复合函数链式求导法则即可,没什么可说的 ,直接上步骤
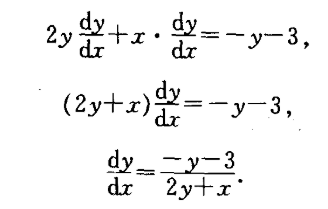
这里我当然都在草稿纸上写了一遍啦嘿嘿 😄
18 相关变化率:你变,我跟着变
相关变化率,我觉得也可以叫做 多隐函数问题
解决这类问题作者提出了一个鸡汤解决法,这里直接概括:
- 熟读
- 画图
- 找到一般式子(关于x 和y 的两个隐含变量的关系)
- 安装17 讲的求微分(直接链式法则作用到复合函数)
- 带入特殊条件
可以拿道例题练练手
用这道题是因为自己做的时候没做出来 😅, 因为漏了个条件,其实就是 step3 没找到,傻了;解应试题还是得有一定的技巧呀
19 求近似值,评估你的成名之路
emmm 很简单了啦,一个图一个式子搞定
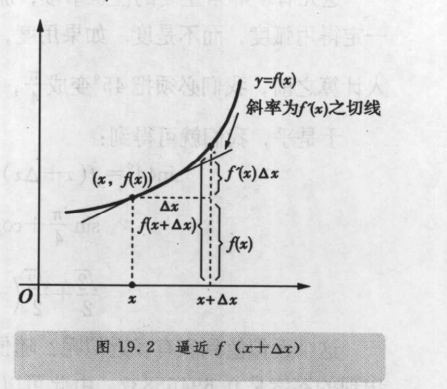
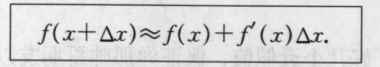
画曲线为直的思想
例:
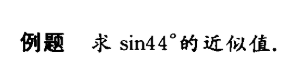
more thinking: sin 72 ° \degree ° 能不能用这种方法做?我的想法是先把sin 1 ° \degree ° 求出来然后用倍角公式,笑死了,也亏我能想出来
20 介值定理与中值定理
介值定理 : 连续的函数中间一定有一个线可以传过去; 当这个线变为 0 的时候事情变得有意思起来
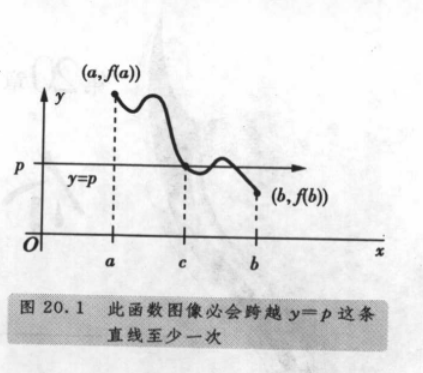
罗尔定理:连续可微 注意一下

中值定理:倾斜过来的罗尔定理
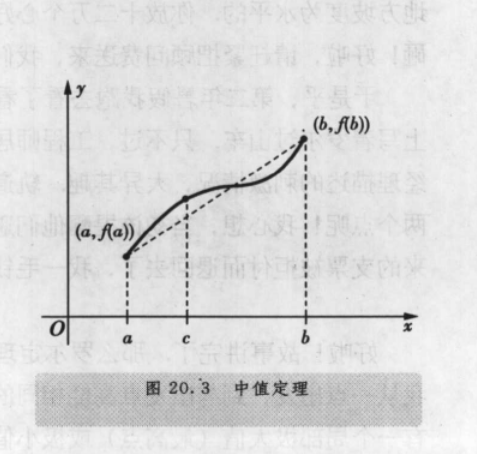
21 积分: 倒过来就成了
不定积分:
- 记得加个常数
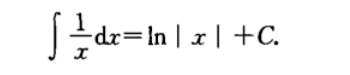
代换法:微分中的链式法则;反过来用
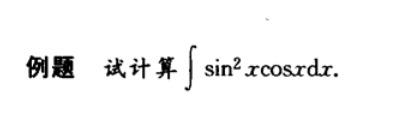
这个好奇怪, 让u 为sin 和cos 的值分别算出来不一样;大概有以下三种解法:
wuli 自己选的三种方法都错了:
第一个是心算的写出来了步骤漏了一项
第二个 是直接做着做着连题目都不管了
第三个 是对代换的概念理解的不够深入: 代换的时候用的是一个函数 而不是一个变量
tips : sin 和cos 乘的时候选高维的代换
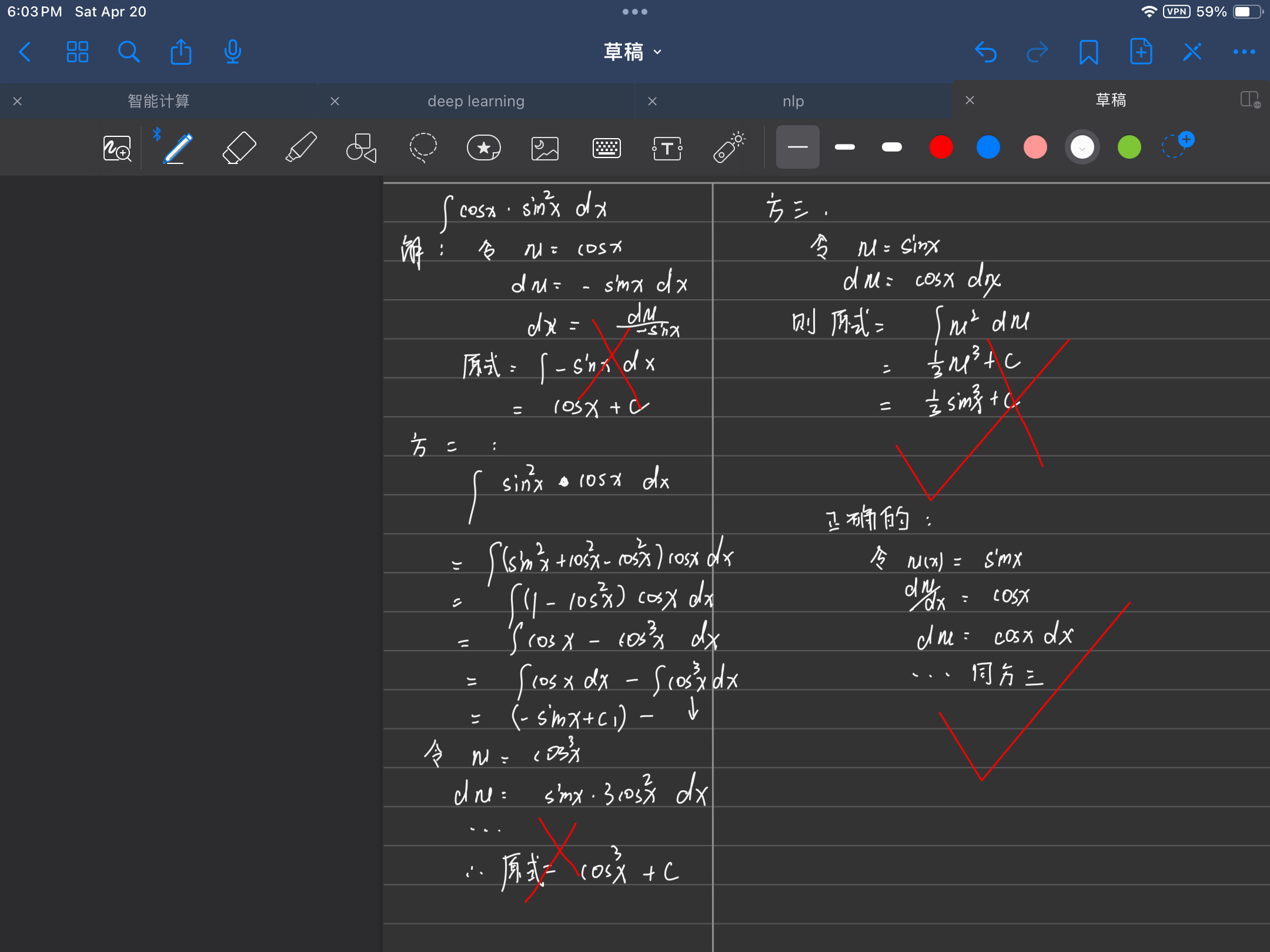
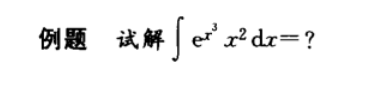
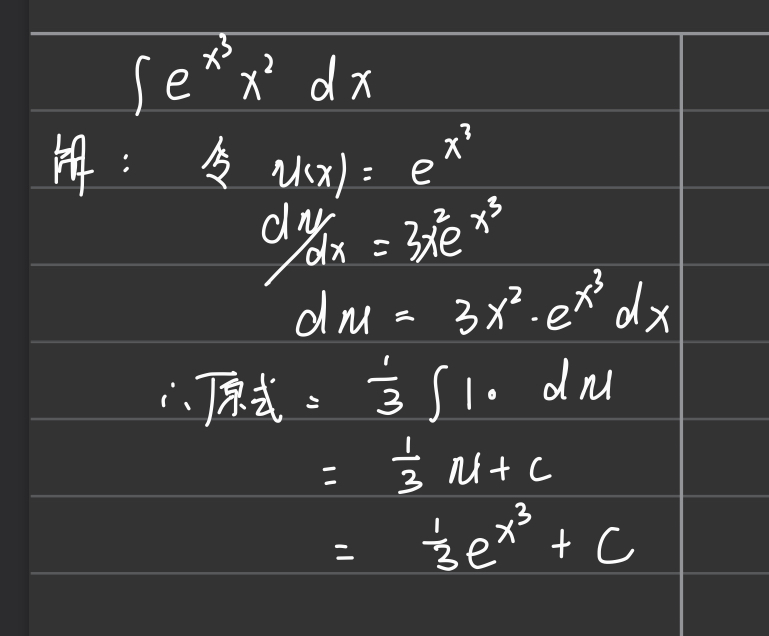
瞪眼法:
就是心算+ 经验 + 猜

积分表:
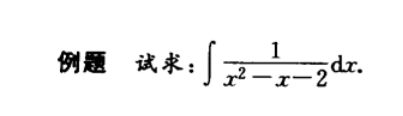
//todo
积分计算器
积分计算器2
22 定积分
我今天体测了,得吃顿好的,兄弟们,别走开,吃饭过后更加精彩~
回来啦 吃了清蒸鲈鱼~ 肉有一丢丢柴,不值88
如何求定积分?
和不定积分一样,把上下限的常数项带进去就行
面积
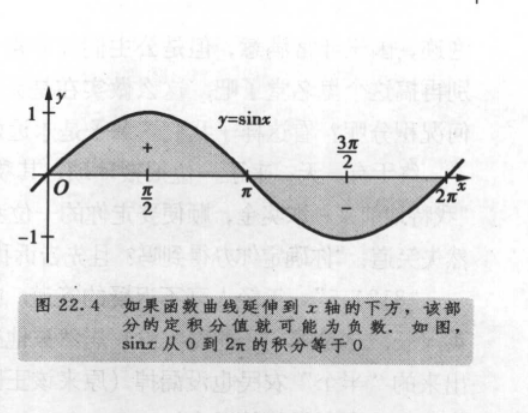
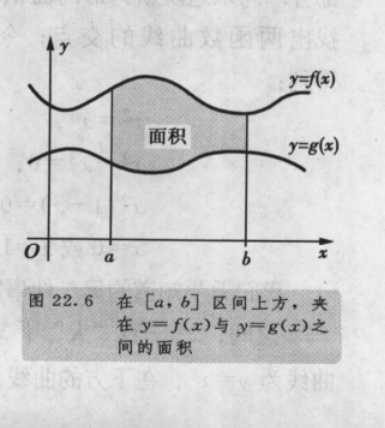
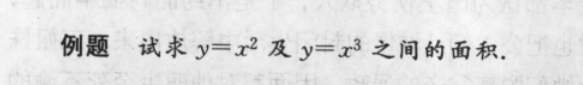
这里x 的绝对值作图时候有点不好画,直接用 绝对值代替
//todo
微积分基本定理1 和 2
为什么可以这样求面积?我靠这个问题我高中的时候其实有想过,下面这个式子为什么成立


可以用来证明微积分基本定理
黎曼和: 曲线下方的面积(若该曲线为正)
定积分的基本法则:
理解成离散的数字求和就比较简单了

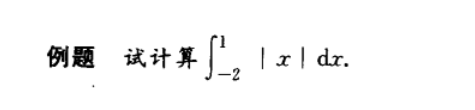
//todo
数值逼近法
怎么说呢, 很抽象的那一层有一点像梯度下降法
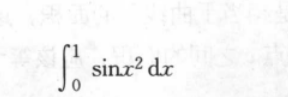

哈哈用计算器解了一下还真好用;ps: 学久了这种传统数学,再看看gpt4.5 感慨科技日新月异的同时也真的赞美数学的美妙啊,历久弥新
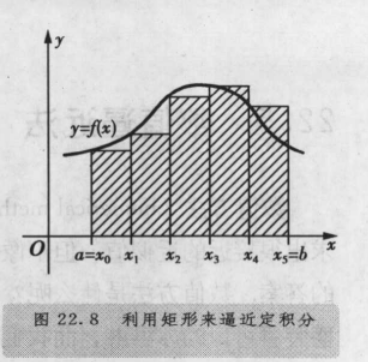


矩形法的左端点法 (最后一项应该停在x n-1 ) 因为是用左边的代替高

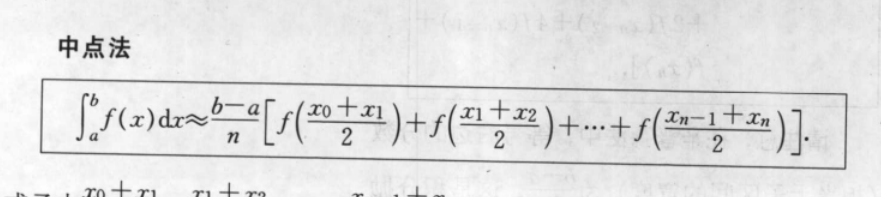
这些矩形就是黎曼和
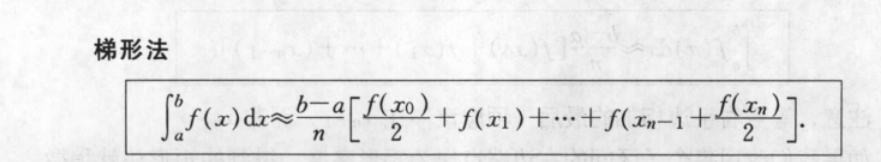
(印刷错误:最后一个括号) 上底+下底的和×高除以2

这里说一下下面两个比较有意思的方法:
梯形法看起来挺奇怪,其实是把前后的上底+下底合并了
//todo
辛普森法: 1 42 42 ……42 41 暂时不知道为啥是这样的模式,有时间推一下
黎曼和 - 附带一些关键细节
定积分的技术定义:
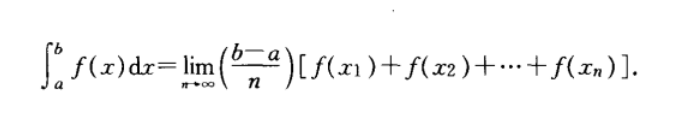
为了挡住门外汉: 引入了求和符$\Sigma $ 和 Δ \Delta Δ x
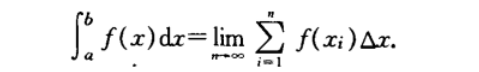
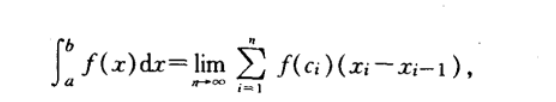
注意区分黎曼和 和上面定积分的技术定义的区别
体现微积分基本定理的好处!
have a break

23 模型:从玩具飞机到跑道
数学模型:
- 大刀阔斧(整理信息,去掉无关信息 )
- 小试牛刀(改造成为一个数学信息)
- 庖丁解牛(求解)
//todo
24 指数于对数: “e”把戏总复习
woc 感觉有点烦躁学不进去了,有点,腿也疼腰也算;java项目的话……emm 也不是不行,试着去学学深度学习或者听听MIT的那个线代课
Engilish
60 个单词背诵
some tips:
it stricks me that to make those words in together,which start with " con" can be devided two parts --“consistent , constant” and others which all means “组成” so that they won’t frustrate my exam annual