1 回溯

1.1 思路及模板

抽象地说，解决一个回溯问题，实际上就是遍历一棵决策树的过程，树的每个叶子节点存放着一个合法答案。你把整棵树遍历一遍，把叶子节点上的答案都收集起来，就能得到所有的合法答案。‘

站在回溯树的一个节点上，你只需要思考 3 个问题：
1、路径：也就是已经做出的选择。
2、选择列表：也就是你当前可以做的选择。
3、结束条件：也就是到达决策树底层，无法再做选择的条件。

回溯算法的框架如下：

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    
    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

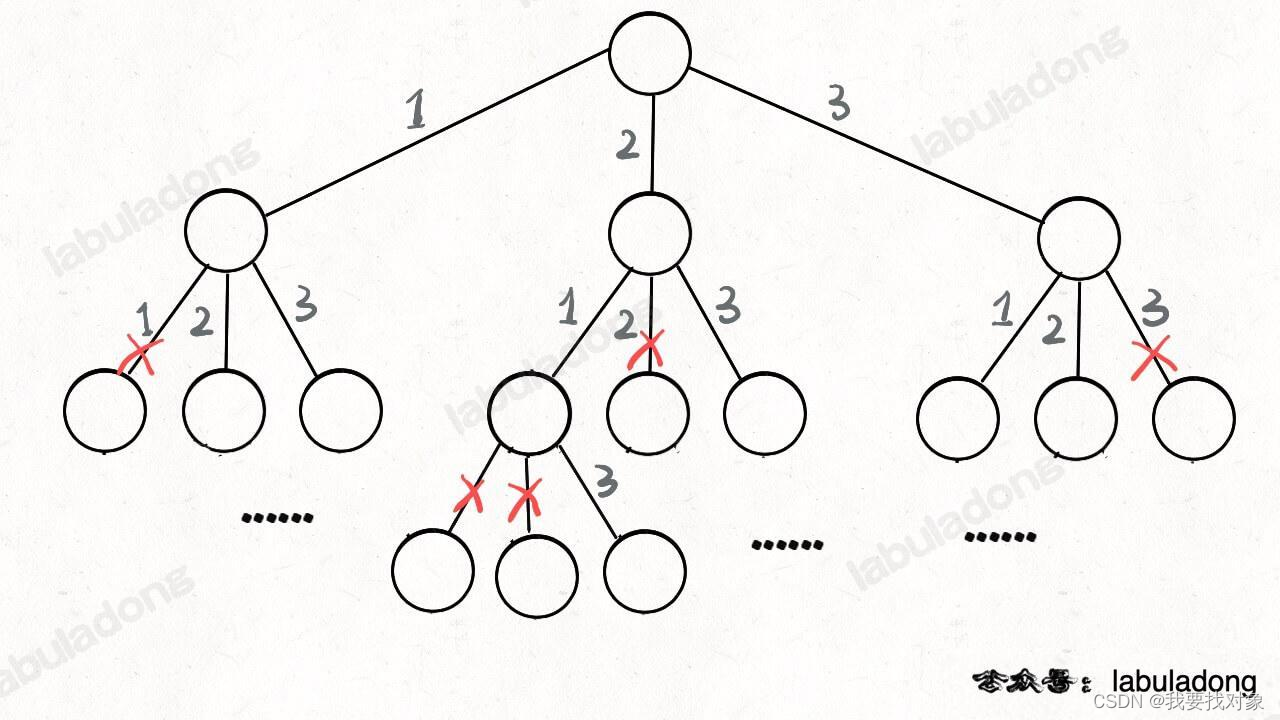
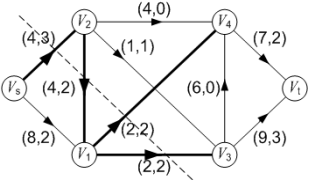
更具体的，在下面的例子中，对于遍历到红色节点来说，现在可以解答开头的几个名词：[2] 就是「路径」，记录你已经做过的选择；[1,3] 就是「选择列表」，表示你当前可以做出的选择；「结束条件」就是遍历到树的底层叶子节点，这里也就是选择列表为空的时候。

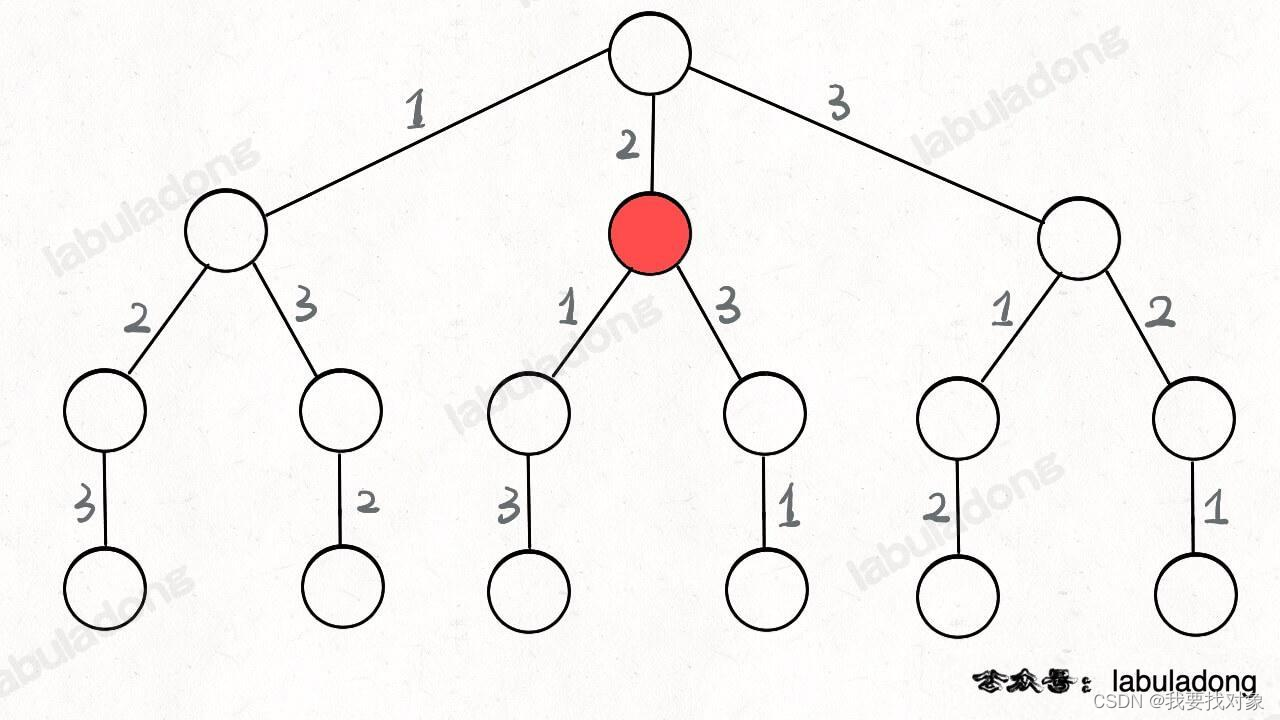
如果明白了这几个名词，可以把「路径」和「选择」列表作为决策树上每个节点的属性，比如下图列出了几个蓝色节点的属性：

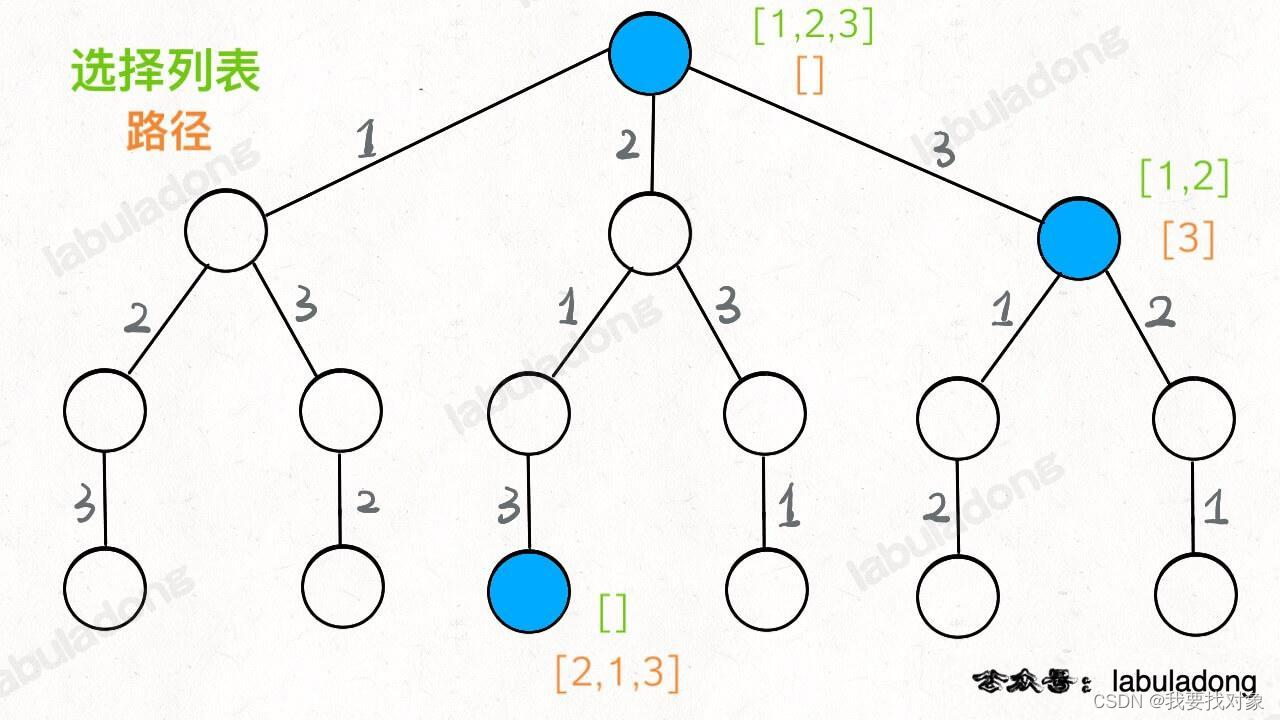
函数在树上游走要正确处理节点的属性，那么就要在这两个特殊时间点搞点动作：

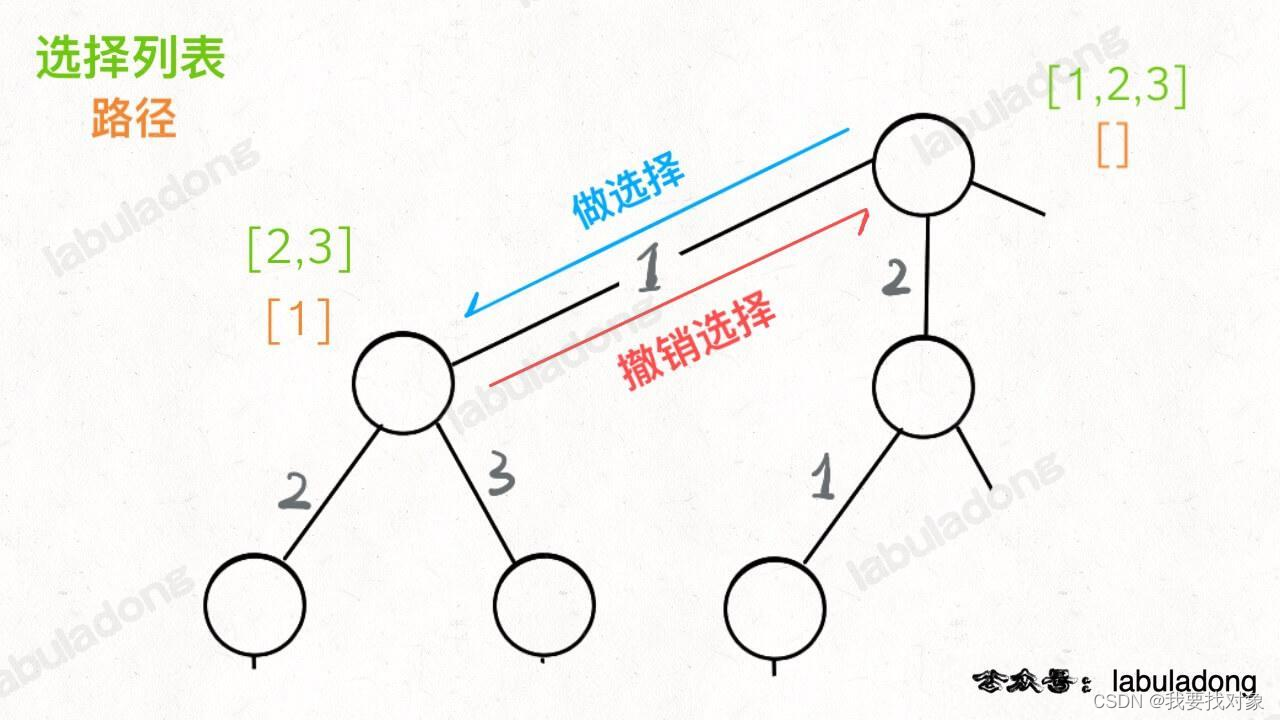
再来理解下回溯框架：

for 选择 in 选择列表:
    # 做选择
    将该选择从选择列表移除
    路径.add(选择)
    backtrack(路径, 选择列表)
    # 撤销选择
    路径.remove(选择)
    将该选择再加入选择列表

1.2 例题

1.2.1 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2：
输入：nums = [0,1]
输出：[[0,1],[1,0]]
示例 3：
输入：nums = [1]
输出：[[1]]

思路以及代码

1、路径：走过的记录在track中。
2、选择列表：used[] 为false表示没走过，可以选择。
3、结束条件：track.size == nums.length 表示到达了叶子节点，可以退出。

class Solution {
    //存放结果
    List<List<Integer>> res = new LinkedList();
    public List<List<Integer>> permute(int[] nums) {
        List<Integer> track = new LinkedList();
        boolean[] used = new boolean[nums.length];
        backtrack(nums,track,used);
        return res;
    }

    // 路径：记录在 track 中
    // 选择列表：nums 中不存在于 track 的那些元素（used[i] 为 false）
    // 结束条件：nums 中的元素全都在 track 中出现
    public void backtrack(int[] nums,List<Integer> track,boolean[] used){
        //当该条路径的track和nums元素相同，也就是已经走到了叶子节点，退出
        if(track.size() == nums.length){
            res.add(new LinkedList(track));
            return ;
        }

        for(int i = 0;i<nums.length;i++){
            //排除不合法
            if(used[i]){
                continue;
            }
            //做选择
            track.add(nums[i]);
            used[i] = true;
            //进入下一层决策树
            backtrack(nums,track,used);
            //退出
            track.removeLast();
            used[i] = false;
        }
    }
}

1.2.2 N 皇后

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例：

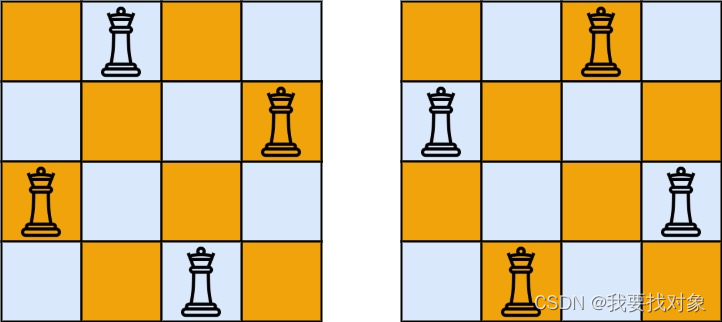
输入：n = 4
输出：[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

思路以及代码：
这个问题本质上跟全排列问题差不多，决策树的每一层表示棋盘上的每一行；每个节点可以做出的选择是，在该行的任意一列放置一个皇后。
路径：board中小于row的行都已经放置了Q
选择列表：board中第row行的所有列都可以选择
结束条件：当超过了最后一行，也就是row = board.size()

class Solution {
public:
    //存放结果
    vector<vector<string>> res;
    vector<vector<string>> solveNQueens(int n) {
        // vector<string> 代表一个棋盘
        // '.' 表示空，'Q' 表示皇后，初始化空棋盘
        vector<string> board(n, string(n, '.'));
        backtrack(board, 0);
        return res;
    }
    //路径：board中小于row的行都已经放置了Q
    //选择列表：board中第row行的所有列都可以选择
    //结束条件：当超过了最后一行，也就是row = board.size()
    void backtrack(vector<string>& board,int row){
        if(board.size() == row){
            res.push_back(board);
            return;
        }
        int n = board[row].size();
        for(int col = 0;col<n;col++){
            // 排除不合法选择
            if (!isValid(board, row, col)) {
                continue;
            }
            // 做选择
            board[row][col] = 'Q';
            // 进入下一行决策
            backtrack(board, row + 1);
            // 撤销选择
            board[row][col] = '.';
        }

    }
    
    //输入棋盘board，判断第row行的第col列是否可以放Q？
    bool isValid(vector<string> board,int row,int col){
        int n = board.size();
        //检查同一列是否有冲突
        for(int i = 0;i<=row;i++){
            if(board[i][col] == 'Q'){
                return false;
            }
        }

        //检查右上
        for(int i = row - 1,j = col + 1;i >= 0 && j < n;i--,j++){
            if(board[i][j] == 'Q'){
                return false;
            }
        }

        //检查左上
        for(int i = row - 1,j = col - 1;i>=0 && j>=0;i--,j--){
            if(board[i][j] == 'Q'){
                return false;
            }
        }
        return true;
    }
};

1.2.3 N皇后问题 II

n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上，并且使皇后彼此之间不能相互攻击。
给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

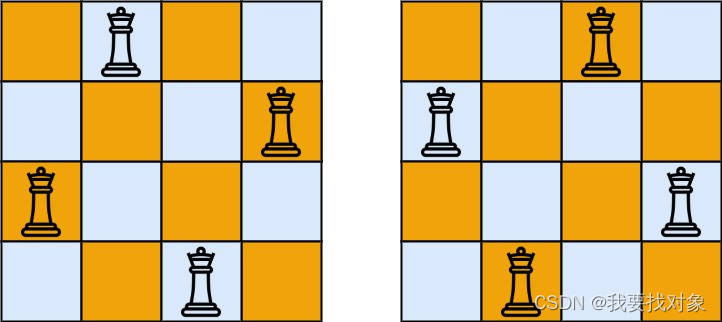
输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

思路以及代码：
这道题和N皇后几乎一样，只需要将N皇后的退出返回数组改为退出res++即可，如下所示：

        if(board.size() == row){
            res++;
            return;
        }