1. 网络最大流
1.1 容量网络和网络最大流
1.1.1 容量网络
设 G(V, E)是一个有向网络,在 V 中指定了一个顶点,称为源点(记为 Vs),以及另一个顶点,称为汇点(记为 Vt);对于每一条弧<u, v>∈ E,对应有一个权值c(u, v)>0,称为弧的容量(capacity)。通常把这样的有向网络 G 称为容量网络。
1.1.2 弧的流量
通过容量网络 G 中每条弧<u, v>上的实际流量(简称流量), 记为 f(u, v)。
1.1.3 网络流
所有弧上流量的集合 f = { f(u, v) },称为该容量网络 G 的一个网络流。
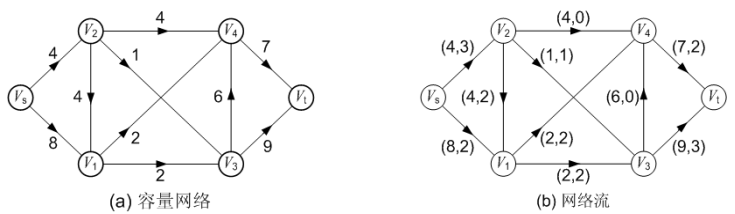
每条弧旁边括号内的两个数值( c(u, v), f(u, v) ),第 1 个数值表示弧容量,第二个数值表示通过该弧的流量。例如,弧<Vs, V1>上的两个数字(8, 2),前者是弧容量,表示通过该弧最大流量为 8,后者表示目前通过该弧的实际流量为 2。
从上图中可见:
-
通过每弧的流量均不超过弧容量;
-
源点 Vs 流出的总量为 3 + 2 = 5,等于流入汇点 Vt 的总量 2 + 3 = 5;
-
其他中间顶点的流出流量等于其流入流量。例如,中间顶 V2 的流入流量为 3,流出流量为: 2 + 1 = 3。
1.1.4 可行流
在容量网络 G(V, E)中,满足以下条件的网络流 f,称为可行流。
-
弧流量限制条件: 0 ≤ f(u, v) ≤ c(u, v), <u, v>∈ E
-
平衡条件:

1.1.5 零流
对于任何一个容量网络,可行流总是在存在的,如 f = { 0 },即每条弧上的流量为 0,该网络流称为零流。
1.1.6 伪流
如果一个网络流只满足弧流量限制条件,不满足平衡条件,则这种网络流称为伪流,或称为容量可行流。
1.1.7 可行流
在容量网络 G(V, E)中,满足弧流量限制条件和平衡条件、且具有最大流量的可行流,称为网络最大流,简称最大流。
1.2 链与增广路
在容量网络 G(V, E)中,设有一可行流 f = { f(u, v) },根据每条弧上流量的多少、以及流量和容量的关系,可将弧分四种类型:
-
饱和弧, 即 f(u, v) = c(u, v);
-
非饱和弧,即 f(u, v) < c(u, v);
-
零流弧, 即 f(u, v) =0;
-
非零流弧,即 f(u, v) > 0。

在上图中,弧<V1, V4>、 <V1, V3>是饱和弧;弧<Vs, V2>、 <V2, V1>等是非饱和弧;弧<V2, V4>、 <V3, V4>是零流弧;弧<V1, V4>、 <V3, Vt>等是非零流弧。
1.2.1 链
在容量网络中,称顶点序列(u, u1, u2, …, un, v)为一条链,要求相邻两个顶点之间有一条弧,如< u, u1 >或< u1, u >为容量网络中一条弧。
设 P 是 G 中从 Vs 到 Vt 的一条链,约定从 Vs 指向 Vt 的方向为该链的正方向。注意,链的概念不等同于有向路径的概念,在链中,并不要求所有的弧都与链的正方向同向。
沿着 Vs 到 Vt 的一条链,各弧可分为两类:
-
前向弧(方向与链的正方向一致的弧),其集合记为 P+;
-
后向弧(方向与链的正方向相反的弧),其集合记为 P–。
注意,前向弧和后向弧是相对的,即相对于指定链的正方向。同一条弧可能在某条链中是前向弧,而在另外一条链中是后向弧。
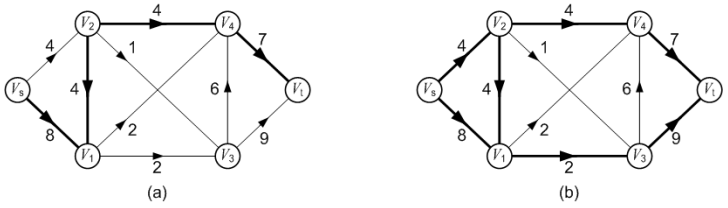
例如在图下中,指定的链为: P = { Vs , V1 , V2 , V4 , Vt },这条链在图(a)中用粗线标明。则P+和 P–分别为:
-
P+ = { <Vs , V1>, <V2 , V4>, <V4, Vt> }。
-
P– = { <V2, V1> }。
1.2.1 增广路
设 f 是一个容量网络 G 中的一个可行流, P 是从 Vs 到 Vt 的一条链,若 P 满足下列条件:
-
在 P 的所有前向弧<u, v>上, 0 ≤ f(u, v) < c(u, v),即 P+中每一条弧都是非饱和弧;
-
在 P 的所有后向弧<u, v>上, 0 < f(u, v) ≤ c(u, v),即 P–中每一条弧是非零流弧。
则称 P 为关于可行流 f 的一条增广路,简称为增广路(或称为增广链、 可改进路)。
那么,为什么将具有上述特征的链 P 称为增广路呢?原因是可以通过修正 P 上所有弧的流量f(u, v)来把现有的可行流 f 改进成一个值更大的流 f1。 沿着增广路改进可行流的操作称为增广。
下面具体地给出一种方法,利用这种方法就可以把 f 改进成一个值更大的流 f1。这种方法是:
不属于增广路 P 的弧<u, v>上的流量一概不变,即 f1(u, v) = f(u, v);
增广路 P 上的所有弧<u, v>上的流量按下述规则变化: (始终满足可行流的 2 个条件)
-
在前向弧<u, v>上, f1(u, v) = f(u, v) +α ;
-
在后向弧<u, v>上, f1(u, v) = f(u, v) -α 。
称 α 为可改进量,它应该按照下述原则确定: α 既要取得尽量大, 又要使变化后 f1 仍满足可行流的两个条件 - 容量限制条件和平衡条件。
不难看出,按照这个原则, α 既不能超过每条前向弧的 c(u, v)– f(u, v),也不能超过每条后向弧的 f(u, v)。 因此 α 应该等于每条前向弧上的 c(u, v)– f(u, v)与每条后向弧上的 f(u, v)的最小值。 即:
![]()
1.3 残留容量与残留网络
1.3.1 残留容量
给定容量网络 G(V, E)及可行流 f,弧<u, v>上的残留容量记为c'(u, v)= c(u, v)– f(u, v)。每条弧的残留容量表示该弧上可以增加的流量。
1.3.2 残留网络
设有容量网络 G(V, E)及其上的网络流 f, G 关于 f 的残留网络(简称残留网络)记为 G'(V', E'), 其中 G'的顶点集 V'和 G 的顶点集 V 相同,即 V'=V,对于 G 中的任何一条弧<u, v>,如果 f(u, v) < c(u, v),那么在 G'中有一条弧<u, v>∈ E',其容量为 c'(u, v) = c(u, v)– f(u, v),如果 f(u, v) > 0,则在 G'中有一条弧<v, u>∈ E',其容量为 c'(v, u) = f(u, v)。 从残留网络的定义可以看出,原容量网络中的每条弧在残留网络中都化为一条或两条弧(如果G中弧<u, v>有残留容量,则在G'中将化为两条弧,一条<u, v>,容量为c(u, v) - f(u, v),一条<v, u>,容量为f(u, v))。

设 f 是容量网络 G(V, E)的可行流, f'是残留网络 G'的可行流,则 f + f'仍是容量网络 G 的一个可行流。 (f + f'表示对应弧上的流量相加)。
1.4 割与最小割
1.4.1 割
在容量网络 G(V, E)中,设 E'⊆ E,如果在 G 的基图中删去 E'后不再连通,则称 E'是 G 的割。割将 G 的顶点集 V 划分成两个子集 S 和 T( V - S)。将割记为(S, T)。
1.4.2 s - t 割
更进一步,如果割所划分的两个顶点子集满足源点 Vs∈ S,汇点 Vt∈ T,则称该割为s-t 割。 s-t 割(S, T)中的弧<u, v>(u∈ S, v∈ T)称为割的前向弧, 弧<u, v>( u∈ T, v∈ S)称为割的反向弧。
1.4.3 割的容量
设(S, T)为容量网络 G(V, E)的一个割, 其容量定义为所有前向弧的容量总和, 用 c(S, T)表示。即:
- c(S, T)=∑ c(u, v) u∈ S, v∈ T, <u, v>∈ E
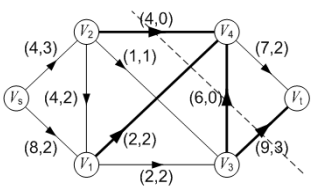
例如在下图中,如果选定 S = { Vs, V1, V2, V3 },则 T = { V4, Vt }, (S, T)就是一个 s-t 割。其容量 c(S, T)为图中粗线边<V2, V4>, <V1, V4>, <V3, V4>, <V3, Vt>的容量总和,即:
- c(S, T) = C24 + C14 + C34 + C3t = 4 + 2 + 6 + 9 = 21
1.4.4 最小割
容量网络 G(V, E)的最小割是指容量最小的割。
1.4.5 割的净流量
设 f 是容量网络 G(V, E)的一个可行流, (S, T)是 G 的一个割, 定义割的净流量 f(S, T)为:
- f(S, T)=∑f(u, v) u∈ S, v∈ T, <u, v>∈ E 或<v, u>∈ E。
注意:
-
在统计割的净流量时:反向弧的流量为负值,即如果<v, u>∈ E,那么在统计割的净流量时 f(u, v)是一个负值。
-
在统计割的容量时:不统计反向弧的容量。
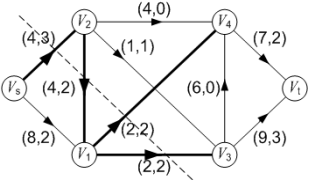
例如,在下图中, S = { Vs, V1 },则 T = { V2, V3, V4, Vt }。
-
割(S, T)的容量 c(S, T)为: c(S, T) = Cs2 + C14 + C13 = 4 + 2 + 2 = 8
-
割(S, T)的净流量为: f(S, T) = fs2 + f21 + f14 + f13 = 3 + (-2) + 2 + 2 = 5
2. 最大流最小割定理
如何判定一个网络流是否是最大流?有以下两个定理。
2.1 增广路定理
设容量网络 G(V, E)的一个可行流为 f, f 为最大流的充要条件是在容量网络中不存在增广路。
2.2 最大流最小割定理
对容量网络 G(V, E),其最大流的流量等于最小割的容量。
![[svelte]属性和逻辑块](https://img-blog.csdnimg.cn/direct/a3e97acb936a4b5c8f1e05dcb610cc87.png)