【每日刷题】Day19

🥕个人主义：开敲🍉

🔥所属专栏：每日刷题🍍

目录

1. 55. 跳跃游戏 - 力扣（LeetCode）

2. 62. 不同路径 - 力扣（LeetCode）

3. 63. 不同路径 II - 力扣（LeetCode）

1. 55. 跳跃游戏 - 力扣（LeetCode）

//思路：从倒数第二个元素开始向前遍历。如果倒数第二个元素为0，则倒数第三个元素至少要为2才能走到终点；如果倒数第三个元素也为0，则倒数第四个元素至少为3才能走到终点，以此类推。当遇到的元素≥count时，说明可以走到终点了，将count重置为0

bool canJump(int* nums, int numsSize)

{

    if(numsSize==1)//如果数组的元素为1，则起点即为终点，直接返回

    {

        return true;

    }

    int count = 0;

    int i = 0;

    for(i = numsSize-2;i>=0;i--)

    {

        if(nums[i]==0&&count==0)//如果倒数第二个元素为0，则+=2，由于后面遇到为0的元素只+=1，因此这里需要加上count来保证只有一次+=2

        {

            count+=2;

        }

        else if(nums[i]<count)//如果遇到的元素不足以抵消count，则count再++

        {

            count++;

        }

        else if(nums[i]>=count)//当足够抵消后，count重置为0

        {

            count = 0;

        }

    }

    if(count!=0)

    {

        return false;

    }

    return true;

}

2. 62. 不同路径 - 力扣（LeetCode）

//0ms 100％思路：画图理解。

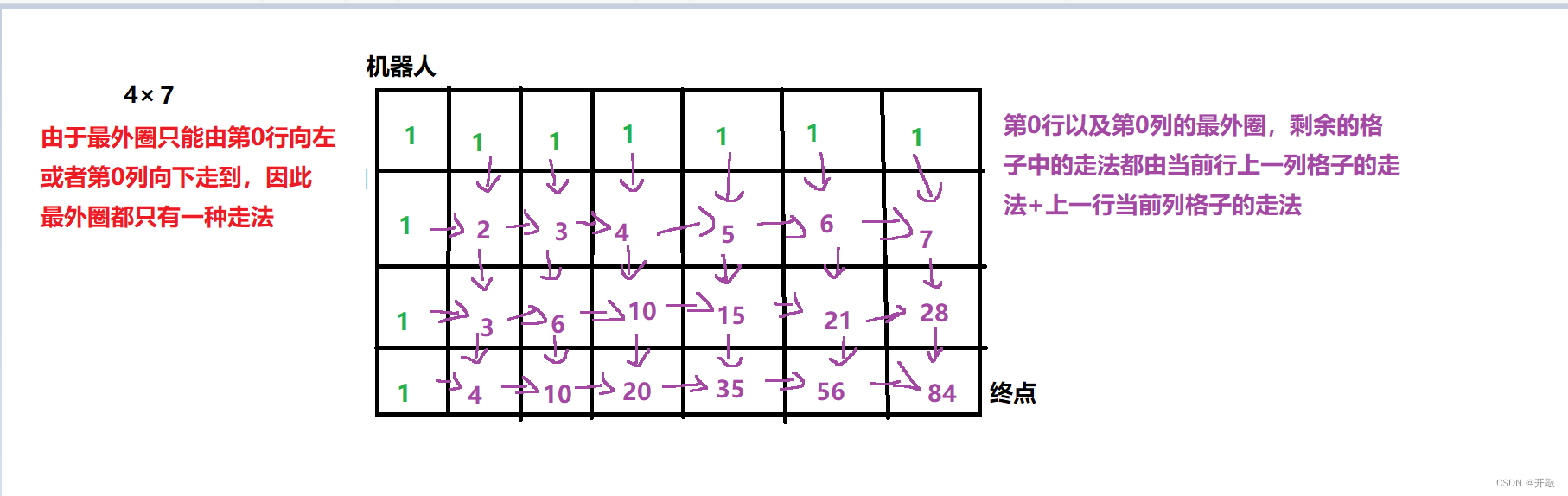
int uniquePaths(int m, int n)

{

    int** arr = (int**)malloc(sizeof(int*)*m);//动态开辟二维数组

    for(int i = 0;i<m;i++)

    {

        arr[i] = (int*)malloc(sizeof(int)*n);//为数组的每一行开辟空间

    }

    for(int i = 0;i<m;i++)

    {

        for(int j = 0;j<n;j++)//将最外圈置为1

        {

            if(i==0||j==0)

            {

                arr[i][j] = 1;

            }

            else

            {

                arr[i][j] = arr[i-1][j]+arr[i][j-1];//最外圈以外的每个格子的走法

            }

        }

    }

    return arr[m-1][n-1];//返回数组最后一个元素的大小即全部走法

}

3. 63. 不同路径 II - 力扣（LeetCode）

//思路：本题和62.不同路径 非常相似，只不过多了障碍物的判断。

int uniquePathsWithObstacles(int** obstacleGrid, int obstacleGridSize, int* obstacleGridColSize)

{

//如果第一个就是障碍物，则没法走，直接返回0

    if(obstacleGrid[0][0]==1)

    {

        return 0;

    }

//动态开辟二维数组

    int** arr = (int**)malloc(sizeof(int*)*obstacleGridSize);

    for(int i = 0;i<obstacleGridSize;i++)

    {

        arr[i] = (int*)malloc(sizeof(int)*(*obstacleGridColSize));

    }

    for(int i = 0;i<obstacleGridSize;i++)

    {

        for(int j = 0;j<(*obstacleGridColSize);j++)

        {

            if(i==0&&j==0&&obstacleGrid[i][j]!=1)//在最外圈放入1，遇到障碍物则不放入

            {

                arr[i][j] = 1;

                continue;

            }

            int tmp1 = 0;

            int tmp2 = 0;

            if((i-1)>=0&&obstacleGrid[i][j]!=1)//最外圈以外当前格子当前行上一列格子的走法，需要判断是否为障碍物

            {

                tmp1 = arr[i-1][j];

            }

            if((j-1)>=0&&obstacleGrid[i][j]!=1)//最外圈以外当前格子上一行当前列格子的走法，同样需要判断是否为障碍物

            {

                tmp2 = arr[i][j-1];

            }

            arr[i][j] = tmp1+tmp2;//当前格子的走法

        }

    }

    return arr[obstacleGridSize-1][(*obstacleGridColSize)-1];//返回终点格子走法

}