完全二叉树

完全二叉树为一类特殊的二叉树，高度为h的完全二叉树满足如下条件：
（1）所有叶结点都出现在第h或h-1层；
（2）第h-1层的所有叶结点都在非叶结点的右边；
（3）除h-1层的最右非叶结点可能有一个左分支外，其余非叶结点都有两个分支

特点：
（1）叶结点只能出现在最底两层，且最底层的叶结点都集中在二叉树的左部；
（2）完全二叉树中至多有1个度为1的结点，如果有，则该结点只有左孩子；
（3）深度为h的完全二叉树的前h-1层一定是满二叉树。

性质：
具有n个结点的完全二叉树的深度为。区中，运算符[x]为对x向下取整。

堆 

现实应用中，经常会遇到频繁地在一组动态数据中获取最大值或最小值的问题。这类问题可以在每次操作时对数据进行排序后获得，但这种方法的时间开销比较大。下面介绍一种可以高效解决这类问题的数据结构--堆。堆有多种形式，包括二叉堆、d-堆、左右堆、斜堆、斐波那契堆、 配对堆等。下面主要介绍二叉堆，为表述简洁，将二叉堆简称为堆。

（动态数据是指需要经常对数据进行更新操作的数据，更新操作包括插入、删除和修改数据）

堆的定义

堆(Heap) 是一类特殊类型的完全二叉树，其每个结点的键值都比其孩子结点的值大（小)，因此，堆的根结点的键值为所有结点键值的最大（小）值。有两种类型的堆：如果根结点的键值为所有结点键值的最大值，则称为最大堆或大顶堆；如果根结点的键值为所有结点键值的最小值，则称为最小堆或小顶堆。

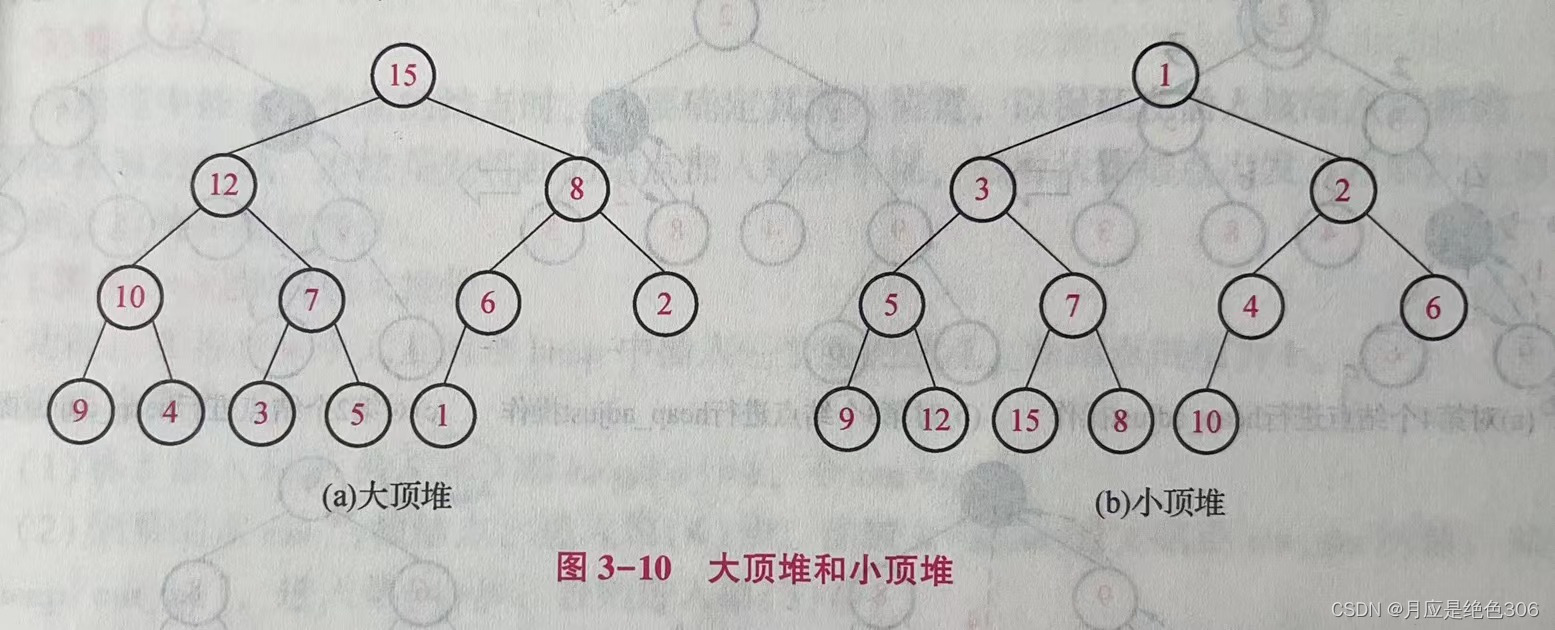
下面介绍大顶堆的性质和操作方法，小顶堆只要稍作修改即可。

#include<iostream>
using namespace std;
typedef int datatype;

//一步操作：在数组heap的前n个元素所构成的完全二叉树中，将以cur为根结点的子树变为大顶堆
/*
	从最后一个非叶结点开始（这样才能进行与孩子结点的比较），从后往前考虑每个结点
	将这每个结点为根结点部分的子树转化为大顶堆（从部分先开始转化为大顶堆）

	需要进行以下的操作：
	1.孩子结点的比较，从大的入手 
	2.父与子结点的比较
	3.若还能向下比较，则注意一开始根结点的数值保存，应在while循环之外

	注意：
	因为每一次转化之前，部分都进行过大顶堆的转换，所以只需要保存每次的最顶上的值，
	依次向下轮换就行，另外注意while循环中cur和i的更新变化
	（i的变化是由于完全二叉树的性质，cur的变化是为了将子节点的较大值赋给父节点，tmp一直保留原先的根结点）
*/
void heap_adjust(datatype heap[], int n, int cur) {
	int i = 0, tmp = heap[cur]; //tmp保留的是根结点数值
	while (i = 2 * cur + 1, i < n) { //i为cur的做孩子
		if (i + 1 < n && heap[i + 1] > heap[i])i++; //孩子结点的比较，heap[i]为较大的孩子结点
		if (heap[i] <= tmp)break;
		heap[cur] = heap[i]; //结点i的值上浮到其父节点
		cur = i; //更新cur
	}
	heap[cur] = tmp;
}
 
//将数组heap的前n个元素所构成的完全二叉树转化为大顶堆
void heap_make(datatype heap[], int n) {
	for (int i = n / 2 - 1; i >= 0; i--)  //由于结点编号从0开始，第一个非叶结点为n/2
		heap_adjust(heap, n, i);
}
 
/*
	插入结点：
	向堆插入一个新的结点时，需要确定其插入的位置，以保证在插入该结点后新的二叉树仍保持堆得特性。
	方法是先将新的结点加入堆的末尾，然后从新的结点出发，自底向上调整二叉树
	思想同转化二叉树
*/
//向堆heap中插入一个值为k的结点，n为堆中元素的个数
void heap_push(datatype heap[],  int k) {
	int cur = 0, pa = 0;
	int n = sizeof(heap) / sizeof(datatype);
	cur = n, n++; //新加入的结点加到heap的末尾，并将其设置为当前结点
	while (cur > 0) {
		pa = (cur - 1) / 2; //结点为cur的父节点
		if (heap[pa] >= k)break;
		heap[cur] = heap[pa]; //当父节点不大于当前结点时，将父节点的值下沉
		cur = pa; //当前结点指向父节点
	}
	heap[cur] = k;
}

/*
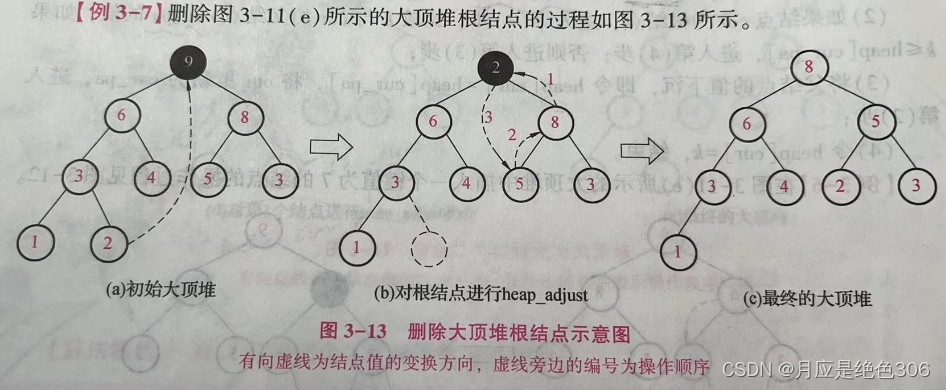
	删除结点
	采用对结构的应用通常是为了快速获取一组动态数据中的最大值或最小值，即获取堆的根结点的值，
	因此，删除堆中的结点也只考虑删除对的根结点。

	方法：
	删除大顶堆根结点的方法是将堆的最后一个结点的值取代根结点的值，并删除最后一个结点，
	然后从根节点出发采用heap_adjust算法将完全二叉树转化为大顶堆
*/
//删除大顶堆heap的根结点，n为堆中元素的数量
void heap_pop(int heap[],int &n) { //n为引用类型，删除堆顶后，堆的元素会减1
	
	heap[0] = heap[n - 1];
	n--;
	heap_adjust(heap, n, 0);
}

int main() {
	datatype a[] = { 2,3,5,1,4,8,3,9,6 };

	//转化为堆
	heap_make(a, 9);
	/*for (int i = 0; i <= 8; i++)
		cout << a[i] << endl;*/
	
	//插入值
	/*heap_push(a, 7);
	for (int i = 0; i <= 8; i++)
		cout << a[i] << endl ;
	cout << endl;*/

	//删除值
	int n = sizeof(a) / sizeof(datatype);
	heap_pop(a,n);
	for (int i = 0; i <= 8; i++)
		cout << a[i] << endl;
}

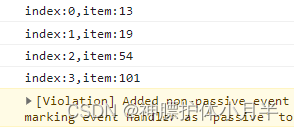
实例展示：（配合上面的代码）

数组转化为大顶堆： 

 大顶堆插入值：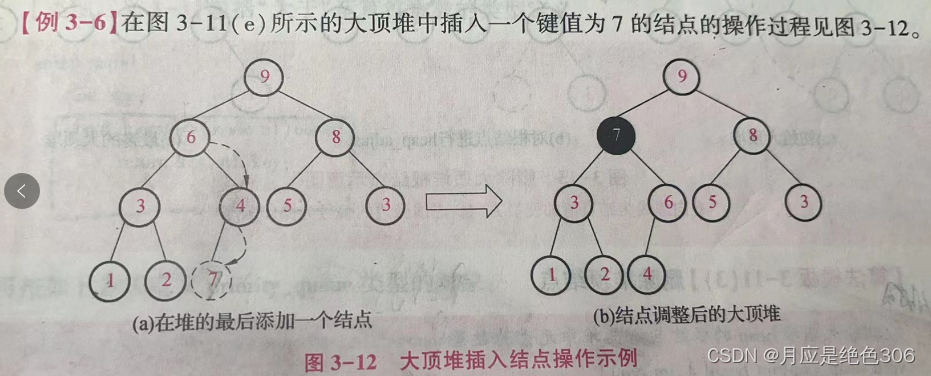

 大顶堆删除值

  STL中的堆——priority_queue

        普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。优先队列是指元素被赋予优先级，在访问元素时，只能访问具有最高优先级的元素，删除元素时也只能删除具有最高优先级的元素。由于每次都获取最高优先级的元素，因此优先队列在底层一般采用堆存储结构，而元素的排序规则是根据优先级从高到低排序。
        STL中集成了优先队列适配器容器prority-queue，支持从一个集合中快速地查找以及删除具有最大值或最小值的元素。priority_queue 可以基于容器deque或vector实现，其默认容器为deque，在使用过程中也可以将容器设置为vector。可分为两种：最小优先队列，适合查找和删除最小元素，类似于小顶堆；最大优先队列，适合查找和删除最大元素，类似于大项堆。在创建priority_queue时默认大顶堆。

使用priority_queue时必须添加头文件

#include<queue>

priority_queue类型的对象定义方法

        一般情况下，priority_queue 有3个类模板参数：第一个模板参数为数据类型，第二个模板参数为基础容器，默认为 deque<类型>类型；第三个模板参数为元素比较的方式，有两种方式：greater<类型＞和 less<类型>，默认为 less<类型>。

        如果元素比较方式使用 less<类型＞，则在用户自定义类型中必须定义“小于“运算符重
载；如果使用greater<类型＞，则在用户自定义类型中必须定义“大于”运算符重载。

priority_queue的操作

和队列基本操作相同:

• top 访问队头元素
• empty 队列是否为空
• size 返回队列内元素个数
• push 插入元素到队尾 (并排序)
• emplace 原地构造一个元素并插入队列
• pop 弹出队头元素
• swap 交换内容

在使用top和pop函数前，一般都需要采用empty函数判断当前优先队列是否为空。

priority_queue实例

1.基本类型例子

#include<iostream>
#include <queue>
using namespace std;
int main()
{
    //对于基础类型 默认是大顶堆
    priority_queue<int> a;
    //等同于 priority_queue<int, vector<int>, less<int> > a;

    priority_queue<int, vector<int>, greater<int> > c;  //这样就是小顶堆，并指定基础类型为vector

    priority_queue<string> b;

    for (int i = 0; i < 5; i++)
    {
        a.push(i);
        c.push(i);
    }

    while (!a.empty())
    {
        cout << a.top() << ' ';
        a.pop();
    }
    cout << endl;

    while (!c.empty())
    {
        cout << c.top() << ' ';
        c.pop();
    }
    cout << endl;

    b.push("abc");
    b.push("abcd");
    b.push("cbd");
    while (!b.empty())
    {
        cout << b.top() << ' ';
        b.pop();
    }
    cout << endl;
    return 0;
}

 2.pari的比较，先比较第一个元素，第一个相等比较第二个

#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int main() 
{
    priority_queue<pair<int, int> > a;
    pair<int, int> b(1, 2);
    pair<int, int> c(1, 3);
    pair<int, int> d(2, 5);
    a.push(d);
    a.push(c);
    a.push(b);
    while (!a.empty()) 
    {
        cout << a.top().first << ' ' << a.top().second << '\n';
        a.pop();
    }
}

3. 对于自定义类型

#include <iostream>
#include <queue>
using namespace std;

//方法1
struct tmp1 //运算符重载<
{
    int x;
    tmp1(int a) {x = a;}
    bool operator<(const tmp1& a) const
    {
        return x < a.x; //大顶堆
    }
};

//方法2
struct tmp2 //重写仿函数
{
    bool operator() (tmp1 a, tmp1 b) 
    {
        return a.x < b.x; //大顶堆
    }
};

int main() 
{
    tmp1 a(1);
    tmp1 b(2);
    tmp1 c(3);
    priority_queue<tmp1> d;
    d.push(b);
    d.push(c);
    d.push(a);
    while (!d.empty()) 
    {
        cout << d.top().x << '\n';
        d.pop();
    }
    cout << endl;

    priority_queue<tmp1, vector<tmp1>, tmp2> f;
    f.push(c);
    f.push(b);
    f.push(a);
    while (!f.empty()) 
    {
        cout << f.top().x << '\n';
        f.pop();
    }
}

总结： 

        优先队列是一种非常有用的数据结构，哈夫曼算法、Dijkstra最短路径算法、Prim最小生成树算法等都采用优先队列实现，另外A*搜索算法和操作系统的线程调度也都使用优先队列。

参考：

1.c++优先队列(priority_queue)用法详解_吕白_的博客-CSDN博客_priority_queue 

2.C++中STL用法超详细总结_list_HUST_Miao-DevPress官方社区 (csdn.net)