一、LeetCode 70. 爬楼梯 (进阶)
题目链接/文章讲解/视频讲解:https://programmercarl.com/0070.%E7%88%AC%E6%A5%BC%E6%A2%AF%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85%E7%89%88%E6%9C%AC.html
状态:已解决
1.思路
这道题跟70.爬楼梯 - 力扣(LeetCode)很像,区别在于此题一次性能爬的台阶数不是固定的,而是题目给定的,因此就不能根据之前的递推式做了。
那我们再来仔细看看这道题,题目给出了需要爬到的楼顶的阶数以及每次可爬的范围。那么这道题实质就是一道完全背包的题:背包容量为n,物品一共m个,且每个物品可以取无限次,问背包装入物品的排列一共有多少种。
那么这道题就被转换成完全背包问题中的排序题了,跟前一天练的组合总和 Ⅳ-CSDN博客中的377题没有区别。
(1)确定dp数组以及下标含义:
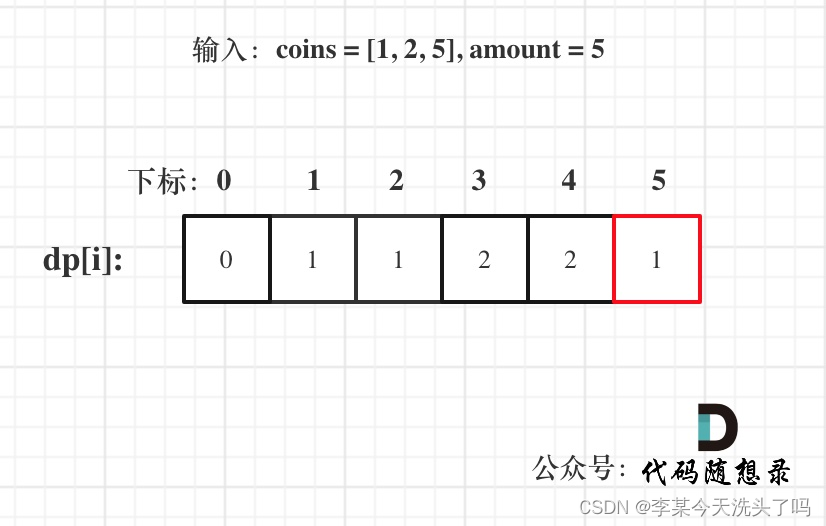
dp[j]: 爬到第 j 层楼梯,有dp[j]种方法。
(2)确定递推式:
dp[i]有几种来源,dp[i - 1],dp[i - 2],dp[i - 3] 等等,即:dp[i - j]。那么递推公式为:dp[i] += dp[i - j]。
(3)dp数组的初始化:
既然递归公式是 dp[i] += dp[i - j],那么dp[0] 一定为1,dp[0]是递归中一切数值的基础所在,如果dp[0]是0的话,其他数值都是0了。
下标非0的dp[i]初始化为0,因为dp[i]是靠dp[i-j]累计上来的,dp[i]本身为0这样才不会影响结果。
(4)确定遍历顺序:
刚刚说了,这是一个求排列的方式,因此外层循环是容量,内层循环是物品。并且完全背包的两层循环都是从前往后遍历。
(5)举例推导dp数组:
和刚刚的377题一致。
2.代码实现
#include<bits/stdc++.h>
using namespace std;
int main(void){
int n,m;
cin>>n>>m;
vector<int> dp(n+1,0);
dp[0] = 1;
for(int j=0;j<=n;j++){
for(int i=1;i<=m;i++){
if(j >= i) dp[j] += dp[j-i];
}
}
cout<<dp[n];
return 0;
}时间复杂度: O(n * m)
空间复杂度: O(n)
二、322. 零钱兑换
题目链接/文章讲解/视频讲解:https://programmercarl.com/0322.%E9%9B%B6%E9%92%B1%E5%85%91%E6%8D%A2.html
状态:已解决
1.思路
做过518. 零钱兑换 II - 力扣(LeetCode)的同学会觉得这两道题很像。确实很像,题目背景是相同的,区别在于518求的是凑钱的所有凑法,而322是求能够凑齐目标金额的最小硬币数。
(1)确定dp数组以及下标含义:
dp[j]:凑足金额为 j 所需钱币的最少个数为dp[j]。
(2)确定递推公式:
凑足总额为 j - coins[i] 的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i] 即dp[j - coins[i]] + 1就是dp[j](考虑coins[i]),因为dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的,因此递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
(3)dp数组的初始化:
首先凑齐金额为0所需的硬币数一定为0,那么其他非0下标呢?由递推公式dp[j] = min(dp[j - coins[i]] + 1, dp[j]);我们知道dp[j]是要与计算值求最小的,故为使计算值不被覆盖,初始值就应该为最大值,即:
vector<int> dp(amount+1,INT_MAX); dp[0] = 0;
(4)确定遍历顺序:
因为本题要求硬币的最少数量,而不是有多少种凑法,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。所以本题并不强调集合是组合还是排列。所以本题的两个for循环的关系是:外层for循环遍历物品,内层for遍历背包或者外层for遍历背包,内层for循环遍历物品都是可以的!
按惯例做法,这里采用coins放在外循环,target在内循环的方式。本题钱币数量可以无限使用,那么是完全背包。故内循环是正序遍历。
(5)举例推导dp数组:
dp[amount]为最终结果。
2.代码实现
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount+1,INT_MAX);
dp[0] = 0;
for(int i=0;i<coins.size();i++){
for(int j=coins[i];j<=amount;j++){
if(dp[j-coins[i]] != INT_MAX)//不为初始值时才做这步
dp[j] = min(dp[j],dp[j-coins[i]]+1);
}
}
//for(int i=0;i<=amount;i++) cout<<dp[i]<<" ";
if(dp[amount] == INT_MAX) return -1;
return dp[amount];
}
};时间复杂度:O(n * amount),n为coins长度
空间复杂度:O(amount)
三、279.完全平方数
题目链接/文章讲解/视频讲解:https://programmercarl.com/0279.%E5%AE%8C%E5%85%A8%E5%B9%B3%E6%96%B9%E6%95%B0.html
状态:已解决
1.思路
换汤不换药,这道题跟上道题如出一辙:给一个容量为n的背包,求装满这个背包最少需要多少物品。物品是什么?就是一个平方数(同个数可以无限使用)。那物品的种类有多少个呢?肯定不超过sqrt(n)个!(sqrt(n)向上取整就是能够凑齐n的平方数的极限值 ),也就是说,上道题的nums[i]在这道题就是 i*i ,除此之外两道题就没有区别了。想清楚了这些,就可以开始写代码了。
(1)确定dp数组以及下标含义:
dp[j]:和为j的完全平方数的最少数量为dp[j]。
(2)确定递推公式:
凑足和为 j - i*i 的最少个数为dp[j - i*i],那么只需要加上一个平方数 i*i 即dp[ j - i*i ] + 1就是dp[j](考虑 i * i),因为dp[j] 要取所有 dp[j -i*i ] + 1 中最小的,因此递推公式:dp[j] = min(dp[j - i * i ] + 1, dp[j]);
(3)dp数组的初始化:
根据题目描述,找到若干个完全平方数(比如 1, 4, 9, 16, ...),并没有从0开始,故给dp[0]=0。
对于非0下标的dp[j],从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]) 中可以看出每次dp[j]都要选最小的,所以非0下标的dp[j]一定要初始为最大值,这样dp[j]在递推的时候才不会被初始值覆盖。
(4)确定遍历顺序:
和上题的分析是一致的
(5)举例推导dp数组:

dp[n]为最终结果。
2.代码实现
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n+1,INT_MAX);
dp[0] = 0;
for(int i=1;i * i<=n;i++){
for(int j=i*i;j<=n;j++){
if(dp[j-i*i] != INT_MAX)
dp[j] = min(dp[j],dp[j-i*i]+1);
}
}
return dp[n];
}
};时间复杂度: O(n * √n)
空间复杂度: O(n)