1、介绍

CAME：一种以置信度为导向的策略，以减少现有内存高效优化器的不稳定性。基于此策略，我们提出CAME同时实现两个目标:传统自适应方法的快速收敛和内存高效方法的低内存使用。大量的实验证明了CAME在各种NLP任务(如BERT和GPT-2训练)中的训练稳定性和优异的性能。

2、Pytorch中调用该优化算法

（1）定义CAME

import math

import torch
import torch.optim

class CAME(torch.optim.Optimizer):
    """Implements CAME algorithm.
    This implementation is based on:
    `CAME: Confidence-guided Adaptive Memory Efficient Optimization`
    Args:
        params (iterable): iterable of parameters to optimize or dicts defining
            parameter groups
        lr (float, optional): external learning rate (default: None)
        eps (tuple[float, float]): regularization constants for square gradient
            and instability respectively (default: (1e-30, 1e-16))
        clip_threshold (float): threshold of root-mean-square of
            final gradient update (default: 1.0)
        betas (tuple[float, float, float]): coefficient used for computing running averages of
        update, square gradient and instability (default: (0.9, 0.999, 0.9999)))
        weight_decay (float, optional): weight decay (L2 penalty) (default: 0)
    """

    def __init__(
        self,
        params,
        lr=None,
        eps=(1e-30, 1e-16),
        clip_threshold=1.0,
        betas=(0.9, 0.999, 0.9999),
        weight_decay=0.0,
    ):
        assert lr > 0.
        assert all([0. <= beta <= 1. for beta in betas])

        defaults = dict(
            lr=lr,
            eps=eps,
            clip_threshold=clip_threshold,
            betas=betas,
            weight_decay=weight_decay,
        )
        super(CAME, self).__init__(params, defaults)

    @property
    def supports_memory_efficient_fp16(self):
        return True

    @property
    def supports_flat_params(self):
        return False


    def _get_options(self, param_shape):
        factored = len(param_shape) >= 2
        return factored

    def _rms(self, tensor):
        return tensor.norm(2) / (tensor.numel() ** 0.5)

    def _approx_sq_grad(self, exp_avg_sq_row, exp_avg_sq_col):
        r_factor = (
            (exp_avg_sq_row / exp_avg_sq_row.mean(dim=-1, keepdim=True))
            .rsqrt_()
            .unsqueeze(-1)
        )
        c_factor = exp_avg_sq_col.unsqueeze(-2).rsqrt()
        return torch.mul(r_factor, c_factor)

    def step(self, closure=None):
        """Performs a single optimization step.
        Args:
            closure (callable, optional): A closure that reevaluates the model
                and returns the loss.
        """
        loss = None
        if closure is not None:
            loss = closure()

        for group in self.param_groups:
            for p in group["params"]:
                if p.grad is None:
                    continue
                grad = p.grad.data
                if grad.dtype in {torch.float16, torch.bfloat16}:
                    grad = grad.float()
                if grad.is_sparse:
                    raise RuntimeError("CAME does not support sparse gradients.")

                state = self.state[p]
                grad_shape = grad.shape

                factored = self._get_options(grad_shape)
                # State Initialization
                if len(state) == 0:
                    state["step"] = 0

                    state["exp_avg"] = torch.zeros_like(grad)
                    if factored:
                        state["exp_avg_sq_row"] = torch.zeros(grad_shape[:-1]).type_as(grad)
                        state["exp_avg_sq_col"] = torch.zeros(
                            grad_shape[:-2] + grad_shape[-1:]
                        ).type_as(grad)

                        state["exp_avg_res_row"] = torch.zeros(grad_shape[:-1]).type_as(grad)
                        state["exp_avg_res_col"] = torch.zeros(
                            grad_shape[:-2] + grad_shape[-1:]
                        ).type_as(grad)
                    else:
                        state["exp_avg_sq"] = torch.zeros_like(grad)

                    state["RMS"] = 0

                state["step"] += 1
                state["RMS"] = self._rms(p.data)

                update = (grad**2) + group["eps"][0]
                if factored:
                    exp_avg_sq_row = state["exp_avg_sq_row"]
                    exp_avg_sq_col = state["exp_avg_sq_col"]

                    exp_avg_sq_row.mul_(group["betas"][1]).add_(
                        update.mean(dim=-1), alpha=1.0 - group["betas"][1]
                    )
                    exp_avg_sq_col.mul_(group["betas"][1]).add_(
                        update.mean(dim=-2), alpha=1.0 - group["betas"][1]
                    )

                    # Approximation of exponential moving average of square of gradient
                    update = self._approx_sq_grad(exp_avg_sq_row, exp_avg_sq_col)
                    update.mul_(grad)
                else:
                    exp_avg_sq = state["exp_avg_sq"]

                    exp_avg_sq.mul_(group["betas"][1]).add_(update, alpha=1.0 - group["betas"][1])
                    update = exp_avg_sq.rsqrt().mul_(grad)

                update.div_(
                    (self._rms(update) / group["clip_threshold"]).clamp_(min=1.0)
                )

                exp_avg = state["exp_avg"]
                exp_avg.mul_(group["betas"][0]).add_(update, alpha=1 - group["betas"][0])

                # Confidence-guided strategy
                # Calculation of instability
                res = (update - exp_avg)**2 + group["eps"][1]

                if factored:
                    exp_avg_res_row = state["exp_avg_res_row"]
                    exp_avg_res_col = state["exp_avg_res_col"]

                    exp_avg_res_row.mul_(group["betas"][2]).add_(
                        res.mean(dim=-1), alpha=1.0 - group["betas"][2]
                    )
                    exp_avg_res_col.mul_(group["betas"][2]).add_(
                        res.mean(dim=-2), alpha=1.0 - group["betas"][2]
                    )

                    # Approximation of exponential moving average of instability
                    res_approx = self._approx_sq_grad(exp_avg_res_row, exp_avg_res_col)
                    update = res_approx.mul_(exp_avg)
                else:
                    update = exp_avg

                if group["weight_decay"] != 0:
                    p.data.add_(
                            p.data, alpha=-group["weight_decay"] * group["lr"]
                        )

                update.mul_(group["lr"])
                p.data.add_(-update)

        return loss

（2）在深度学习中调用CAME优化器

本文以使用LSTM算法对鸢尾花数据集进行分类为例，并且在代码中加入早停和十折交叉验证技术。

import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import load_iris
from sklearn.model_selection import StratifiedKFold
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score

# 定义 LSTM 模型
class LSTMClassifier(nn.Module):
    def __init__(self, input_size, hidden_size, num_classes):
        super(LSTMClassifier, self).__init__()
        self.lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_size, batch_first=True)
        self.fc = nn.Linear(hidden_size, num_classes)
    
    def forward(self, x):
        _, (hn, _) = self.lstm(x)
        out = self.fc(hn[-1])  # 选择最后一个 LSTM 隐层输出
        return out

# 早停
class EarlyStopping:
    def __init__(self, patience=5, min_delta=0):
        self.patience = patience
        self.min_delta = min_delta
        self.best_loss = float('inf')
        self.counter = 0
        self.early_stop = False

    def step(self, val_loss):
        if val_loss < self.best_loss - self.min_delta:
            self.best_loss = val_loss
            self.counter = 0
        else:
            self.counter += 1
            if self.counter >= self.patience:
                self.early_stop = True

# 读取数据
iris = load_iris()
X = iris.data
y = iris.target

# 标准化数据
scaler = StandardScaler()
X = scaler.fit_transform(X)

# 将数据转换为 PyTorch 张量
X = torch.tensor(X, dtype=torch.float32)
y = torch.tensor(y, dtype=torch.long)

# 配置模型参数
input_size = X.shape[1]  # 特征数量
hidden_size = 32
num_classes = 3
batch_size = 16
num_epochs = 100
learning_rate = 0.001
patience = 5

# 进行十折交叉验证
kf = StratifiedKFold(n_splits=10, shuffle=True, random_state=42)
fold_idx = 0

for train_index, val_index in kf.split(X, y):
    fold_idx += 1
    print(f"Fold {fold_idx}")

    # 划分训练集和验证集
    X_train, X_val = X[train_index], X[val_index]
    y_train, y_val = y[train_index], y[val_index]

    # 定义模型和优化器
    model = LSTMClassifier(input_size, hidden_size, num_classes)
    optimizer = CAME(model.parameters(), lr=2e-4, weight_decay=1e-2, betas=(0.9, 0.999, 0.9999), eps=(1e-30, 1e-16))
    # optimizer = optim.Adam(model.parameters(), lr=learning_rate)
    criterion = nn.CrossEntropyLoss()

    # 早停设置
    early_stopping = EarlyStopping(patience=patience)

    # 训练模型
    for epoch in range(num_epochs):
        # 训练阶段
        model.train()
        optimizer.zero_grad()
        outputs = model(X_train.unsqueeze(1))
        loss = criterion(outputs, y_train)
        loss.backward()
        optimizer.step()
        
        # 验证阶段
        model.eval()
        with torch.no_grad():
            val_outputs = model(X_val.unsqueeze(1))
            val_loss = criterion(val_outputs, y_val)
        
        # 打印每轮迭代的损失值
        print(f"Epoch {epoch + 1}: Train Loss = {loss.item():.4f}, Val Loss = {val_loss.item():.4f}")

        # 早停检查
        early_stopping.step(val_loss.item())
        if early_stopping.early_stop:
            print(f"Early stopping at epoch {epoch + 1}")
            break
    
    # 评估模型
    model.eval()
    with torch.no_grad():
        val_outputs = model(X_val.unsqueeze(1))
        _, predicted = torch.max(val_outputs, 1)
        accuracy = accuracy_score(y_val, predicted)
        print(f"Fold {fold_idx} Validation Accuracy: {accuracy:.4f}\n")

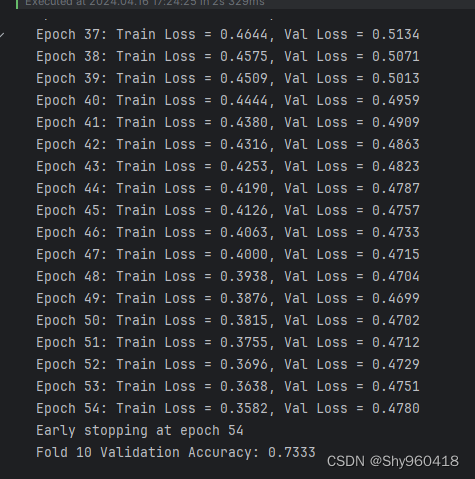
由于CAME主要面向NLP数据集，因此对于鸢尾花效果不算好，本文仅展示CAME的使用方法，并非提升acc和epoch。

参考文献：Luo, Yang, et al. “CAME: Confidence-guided Adaptive Memory Efficient Optimization.” arXiv preprint arXiv:2307.02047 (2023).