目录

一、PCA主成分分析

二、PCA人脸识别

三、结果

---

一、PCA主成分分析

PCA（主成分分析）是一种非常常用的数据降维技术。它通过线性变换将原始数据变换到一个新的坐标系统中，使得在这个新坐标系统的第一个坐标轴上的数据方差最大，第二个坐标轴上的数据方差次之，依此类推，以达到降维的目的。下面是更详细的步骤和解释：

1. 中心化数据：首先将数据的每一维度都减去其均值，这样每一维的均值变为0。

2. 计算协方差矩阵：在中心化后的数据基础上，计算协方差矩阵。协方差矩阵反映了数据中各维度间的相关性。

3. 求解特征值和特征向量：计算协方差矩阵的特征值和对应的特征向量。这些特征向量代表了数据中的主要变化方向，而特征值的大小表示了各个方向上变化的程度。

4. 选择主成分：一般会根据特征值的大小，从大到小选择前几个特征向量，这些特征向量称为“主成分”。通常选择的主成分数量取决于所需保留的原始数据信息量的百分比。

5. 投影到新的空间：将原始数据投影到这些主成分构成的空间中，即可实现数据的降维。

二、PCA人脸识别

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as scio
import matplotlib.image as mpimg  # 读入图片
import mpl_toolkits.mplot3d as Axes3D  # 用来画三维图

'''============================part1 数据导入及可视化========================='''

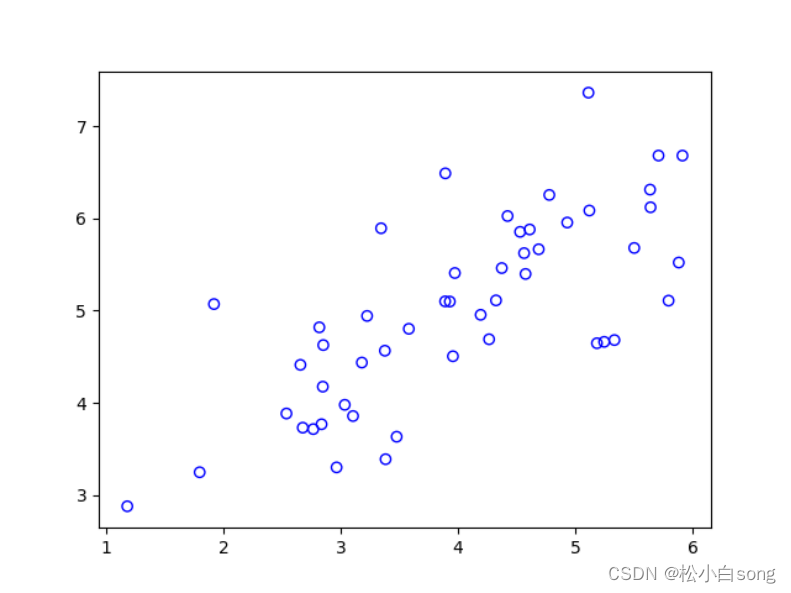
data = scio.loadmat('data_sets/ex7data1.mat')
x = data['X']
plt.scatter(x[:, 0], x[:, 1], marker='o', facecolors='none', edgecolors='b')

'''============================part2 PCA===================================='''
'''数据标准化'''


def featureNormalize(x):
    mu = x.mean(axis=0)  # 求每列的
    sigma = x.std(axis=0, ddof=1)  # 无偏的标准差，自由度为n-1
    x_norm = (x - mu) / sigma
    return x_norm, mu, sigma


x_norm, mu, sigma = featureNormalize(x)

'''得到特征向量和特征值'''


def pca(x):
    m, n = x.shape
    Sigma = (x.T @ x) / m  # 协方差矩阵
    U, S, V = np.linalg.svd(Sigma)  # SVD奇异值分解
    return U, S


U, S = pca(x_norm)

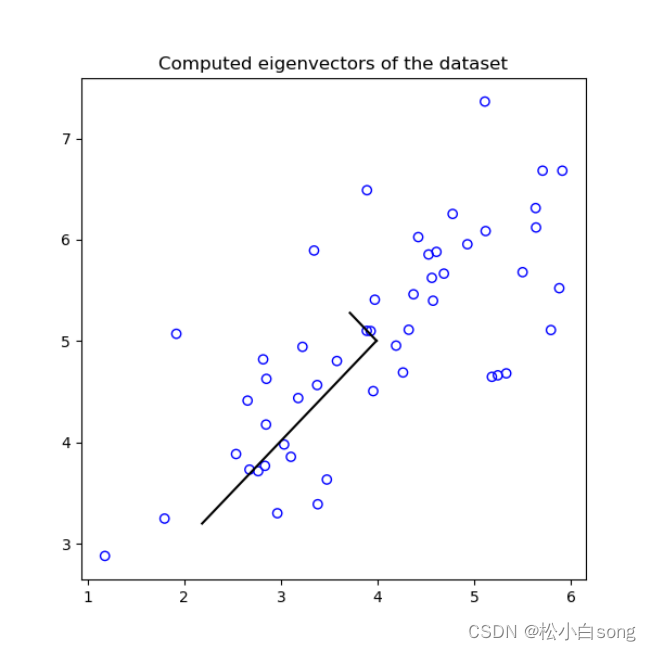
# 画出特征向量
plt.figure(figsize=(6, 6))
plt.scatter(x[:, 0], x[:, 1], marker='o', facecolors='none', edgecolors='b')
plt.plot([mu[0], mu[0] + 1.5 * S[0] * U[0, 0]], [mu[1], mu[1] + 1.5 * S[0] * U[1, 0]], 'k')  # 两个点的连线
plt.plot([mu[0], mu[0] + 1.5 * S[1] * U[0, 1]], [mu[1], mu[1] + 1.5 * S[1] * U[1, 1]], 'k')  # 这里的1.5和S表示特征向量的长度
plt.title('Computed eigenvectors of the dataset')

'''============================part3 降维========================='''
'''降维，数据投影到特征向量上'''


def projectData(x, U, K):
    U_reduce = U[:, 0:K]
    return x @ U_reduce


# 降维后的数据，(50, 1)
z = projectData(x_norm, U, 1)
z[0]  # 1.48127391

'''重建数据'''


def recoverData(z, U, K):
    U_reduce = U[:, 0:K]
    return z @ U_reduce.T  # 因为U是特征向量矩阵，由标准正交基组成，U.T@U为单位矩阵


# 重建后的数据
x_rec = recoverData(z, U, 1)
x_rec[0, :]  # [-1.04741883, -1.04741883]

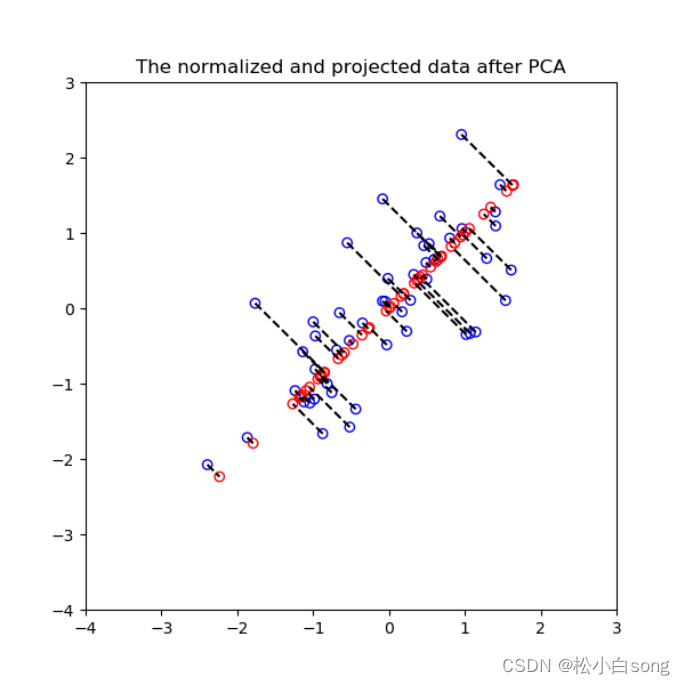
# 可视化投影
plt.figure(figsize=(6, 6))
plt.xlim((-4, 3))
plt.ylim((-4, 3))
plt.scatter(x_norm[:, 0], x_norm[:, 1], marker='o', facecolors='none', edgecolors='b')
plt.scatter(x_rec[:, 0], x_rec[:, 1], marker='o', facecolors='none', edgecolors='r')
for i in range(len(x_norm)):
    plt.plot([x_norm[i, 0], x_rec[i, 0]], [x_norm[i, 1], x_rec[i, 1]], 'k--')
plt.title('The normalized and projected data after PCA')

'''保留了多少差异性'''


def retained_variance(S, K):
    rv = np.sum(S[:K]) / np.sum(S)
    return print('{:.2f}%'.format(rv * 100))


# 看看降维后保留了多少差异性
retained_variance(S, 1)  # 86.78%

'''============================part4 人脸数据导入及可视化========================='''
data = scio.loadmat('data_sets/ex7faces.mat')
x = data['X']

'''人脸可视化'''


def displayData(x):
    plt.figure()
    n = np.round(np.sqrt(x.shape[0])).astype(int)
    # 定义n*n的子画布
    fig, a = plt.subplots(nrows=n, ncols=n, sharex=True, sharey=True, figsize=(6, 6))
    # 在每个子画布中画出一个图像
    for row in range(n):
        for column in range(n):
            a[row, column].imshow(x[n * row + column].reshape(32, 32).T, cmap='gray')
    plt.xticks([])  # 去掉坐标轴
    plt.yticks([])


# 可视化前100个人脸
displayData(x[0:100, :])

'''============================part5 在人脸数据上实施PCA========================='''
# 数据标准化
x_norm, mu, sigma = featureNormalize(x)
# 特征向量
U, S = pca(x_norm)
# 可视化前36个特征向量
displayData(U[:, 0:36].T)

'''============================part6 人脸数据降维以及可视化========================='''
# 将原始数据降至100维
K = 100
z = projectData(x_norm, U, K)
z.shape  # (5000, 100)
# 重建后的数据
x_rec = recoverData(z, U, K)  # (5000, 1024)

# 画图对比
displayData(x[0:100, :])
displayData(x_rec[0:100, :])

# 看看降维后保留了多少差异性
retained_variance(S, K)  # 93.19%

'''============================part7 PCA用在数据可视化========================='''
# 读取图片
A = mpimg.imread('data_sets/bird_small.png')  # 读取图片

'''k-means的代码'''


def findClosestCentroids(x, centroids):
    idx = np.zeros(len(x))
    for i in range(len(x)):
        c = np.sqrt(np.sum(np.square((x[i, :] - centroids)), axis=1))  # 行求和
        idx[i] = np.argmin(c) + 1
    return idx


def computeCentroids(x, idx, K):
    mu = np.zeros((K, x.shape[1]))
    for i in range(1, K + 1):
        mu[i - 1] = x[idx == i].mean(axis=0)  # 列求均值
    return mu


def kMeansInitCentroids(x, K):
    randidx = np.random.permutation(x)  # 随机排列
    centroids = randidx[:K, :]  # 选前K个
    return centroids


# 运行k-means
def runKmeans(x, centroids, max_iters):
    for i in range(max_iters):
        idx = findClosestCentroids(x, centroids)  # 簇分配
        centroids = computeCentroids(x, idx, len(centroids))  # 移动聚类中心
    return centroids, idx


# k-means部分
X = A.reshape(A.shape[0] * A.shape[1], 3)
K = 16  # 聚类数量
max_iters = 10  # 最大迭代次数
initial_centroids = kMeansInitCentroids(X, K)  # 初始化聚类中心
centroids, idx = runKmeans(X, initial_centroids, max_iters)  # 得到聚类中心和索引
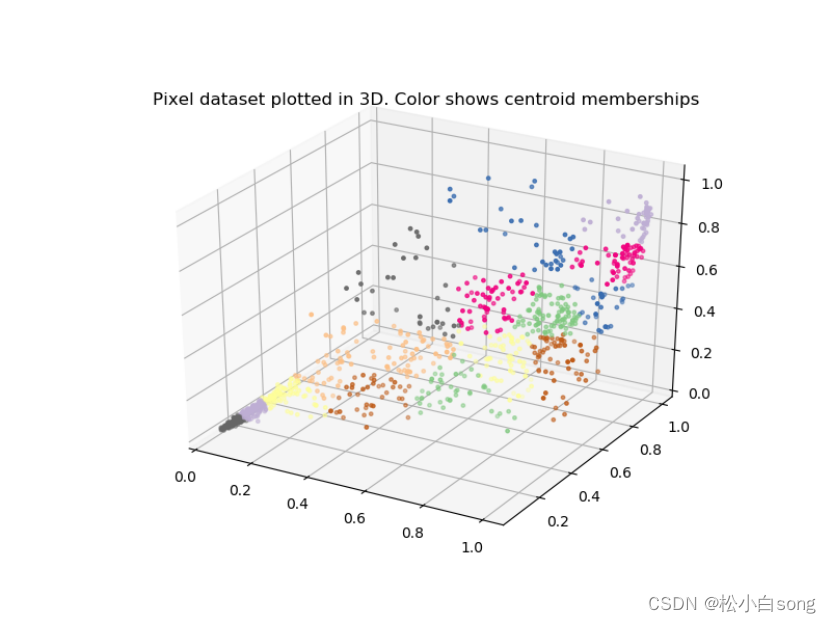
sel = np.random.randint(X.shape[0], size=1000)  # 随机选择1000个样本
cm = plt.cm.get_cmap('Accent')  # 设置颜色

# 画三维图
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')  # “111”表示“1×1网格，第一子图”
ax.scatter(X[sel, 0], X[sel, 1], X[sel, 2], c=idx[sel], cmap=cm, s=6)
plt.title('Pixel dataset plotted in 3D. Color shows centroid memberships')

# PCA部分
X_norm, mu, sigma = featureNormalize(X)  # 标准化
U, S = pca(X_norm)  # 特征向量
Z = projectData(X_norm, U, 2)  # 投影降维

# 画二维图
plt.figure(figsize=(8, 6))
plt.scatter(Z[sel, 0], Z[sel, 1], c=idx[sel], cmap=cm, s=7)
plt.title('Pixel dataset plotted in 2D, using PCA for dimensionality reduction')

# 看看降维后保留了多少差异性
retained_variance(S, 2)  # 99.34%
plt.show()  #可视化

三、结果