1.简单介绍
2.思想的实际运用
我们利用蒙特卡罗法的思想求解圆周率π的值,这里求得的肯定是近似值,我们是通过大量的模拟实验,利用概率求解的,但是这个值和我们的精确值之间还是有一定的误差的;
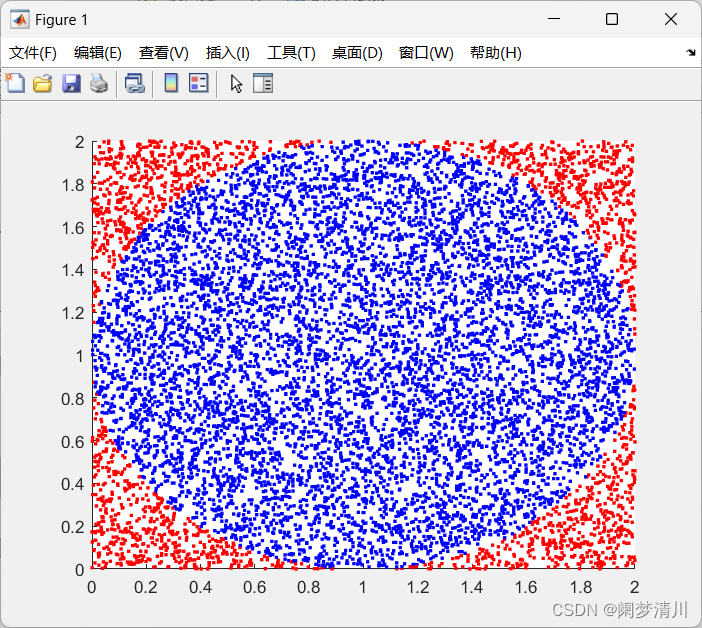
我们的思想就是在半径为1的圆的外面做一个外切正方形,这个外切正方形的边长就是2,那么我们想要求的圆的面积π乘上半径的平方实际上就是乘以1的平方,也就是说圆的面积就是π,我们在这个正方形上面撒豆子,这个豆子可能会落在圆形里面,我们根据落在圆形里面的豆子数量占全部正方形里面的豆子的数量的比例,来计算这个圆形的面积,也就是我们的π,假设我们撒了10000颗豆子,有8000颗落在圆形里面,我们直接拿4*80%就是圆形的面积,也就是我们的π的近似值,这样的求解方法实际上就是蒙特卡罗法。前提是我们的实验的次数足够多,也就是说我们的豆子的数量应该足够多,这样进行实验得到的结论才具有普遍性,更有说服力。
3.MATLAB代码逐句分析
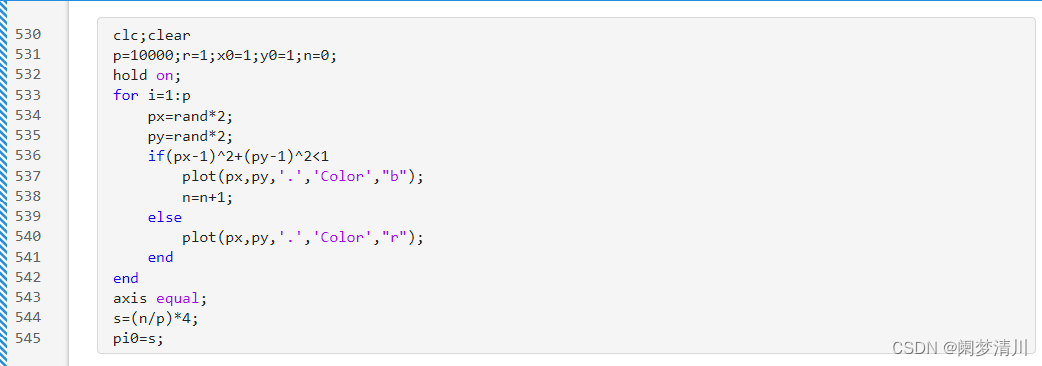
这个就是求解圆周率π需要用到的代码,我们分析一下:
(1)clc;clear是清除工作区的命令,这个命令我们已经很常见了,我们建议写上这句命令,这样就可以避免不必要的报错,因为在工作区里面可能我们前面定义的某一个变量和我们这个代码的变量会冲突,我们尽量使用这句话清除工作区的数据;
(2)p就是我们的实验进行的次数,通俗的讲就是我们的要撒的豆子的总量10000,这个数据比较大,结论具有普遍性;
(3)我们接下来使用for循环进行计数,这个里面的rand是一个函数,这个函数的作用就是生成随机数,随机数就可以具有普遍性,减少我们人为因素的影响,在其他的编程语言里面也会用到这个随机数的生成函数,例如我们熟知的扫雷游戏,这个游戏需要随机的布置地雷,这个时候就要设置地雷的坐标,这个地方也用到了rand函数,我们的MATLAB里面的rand函数默认的生成随机数字的范围是0~1,前面我们已经提及过,这个正方形的边长是2,我们让圆心的坐标是(1,1),所以我们让rand*2,这样的话生成的随机数的范围就是0~2之间(横坐标和纵坐标都在0~2之间),正好是落在我们的正方形区域里面;
(4)n表示这个时候落在圆形里面的豆子的数量,因为我们在进行参数的设置,这个时候还没有开始进行,相当于我们定义了一个变量n用来存储落在圆形里面的豆子数量,将来进行循环的时候,符合条件的在0的基础上面进行累加就可以了,这个n就相当于是一个计数器的角色;
(5)这个if语句是计算正方形里面的点到圆心的距离,如果距离小于半径的平方,说明这个循环产生的随机数在圆形里面,我们就是用n累加这个数;plot就是绘图指令,符合条件的和不符合条件的我们需要使用不同的标志进行绘图以方便区分;
(6)这个里面我们一共是进行了10000次循环,每次循环都会产生随机数,每次都会使用if语句进行判断,符合条件的话(豆子落在圆形区域里面),就让n加上1,然后绘制圆形里面的图,否则的话就绘制图圆形和正方形之间的图;plot里面的高亮部分就是一些plot函数的固定参数,我们了解即可,参数的最后一项就是图形颜色的设置,像我们这个里面用到的r表示的是红色,b表示的是蓝色;
(7)axis equal就是让我们的绘制出来的图形的横纵坐标轴的标度是一样的,这样的图像就会更加的美观,我在下面分别放了加上这句代码和不加这句代码的效果图,显然加上这个代码会更好;
(8)n/q就是我们的对应的概率,我们使用这个概率乘上正方形的面积4就是对应的圆形的面积,也就是我们想要计算的圆周率π,这个方法的本质就是概率;最后我们把s的值赋值给pi0,这样pio里面就是我们计算出来的圆周率的近似值;
(9)里面还有一行代码我们没有提到,就是这句hold on,这个代码到底是什么作用,我相信很多初学者都不是很清楚(我也是今天才知道);现在请你记住,这个代码的作用就是让我们每次循环的图像都在一个图像里面进行绘制,换言之,如果没这句代码,我们要进行10000次循环,每次循环都会产生新的窗口,这样的话我们无法进行观察,加上这句代码我们就可以让每次循环绘制的点在一个图里面,方便我们进行观察。
加上axis equal效果:

不加axis equal的效果: