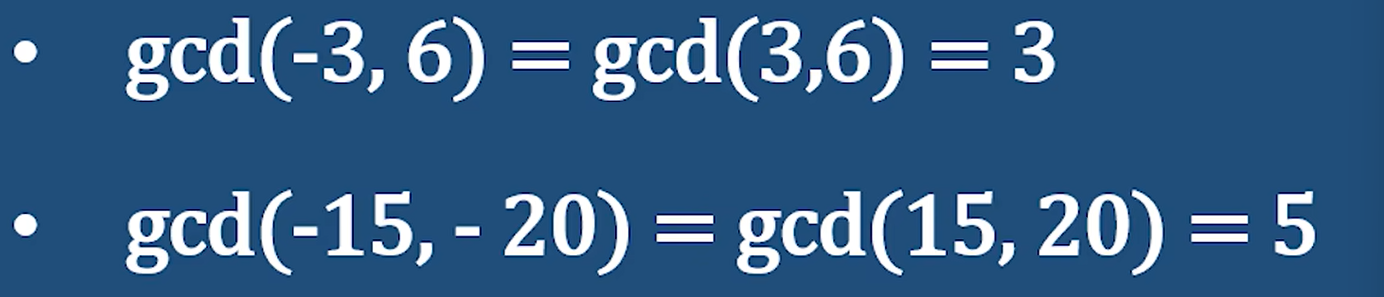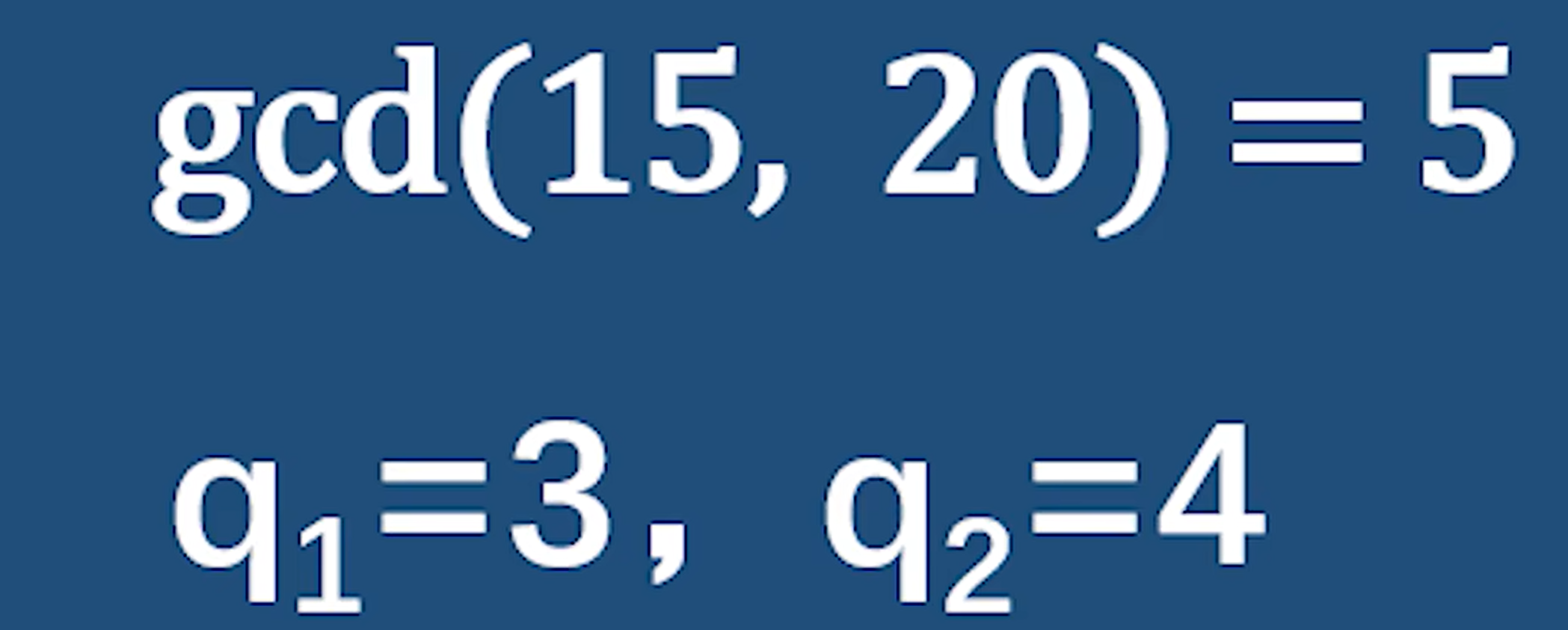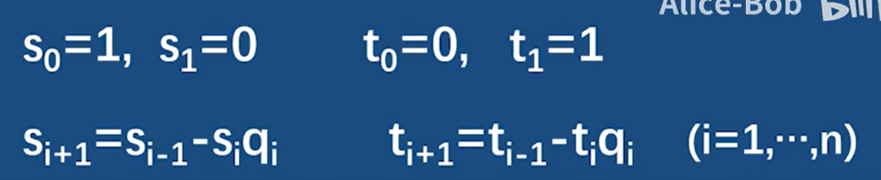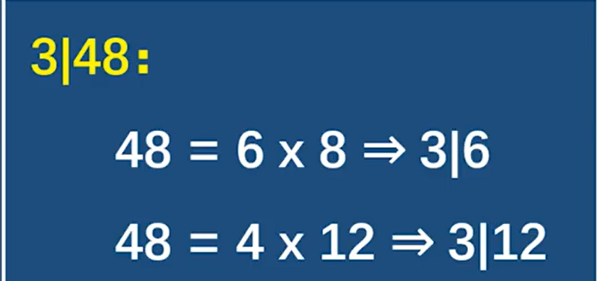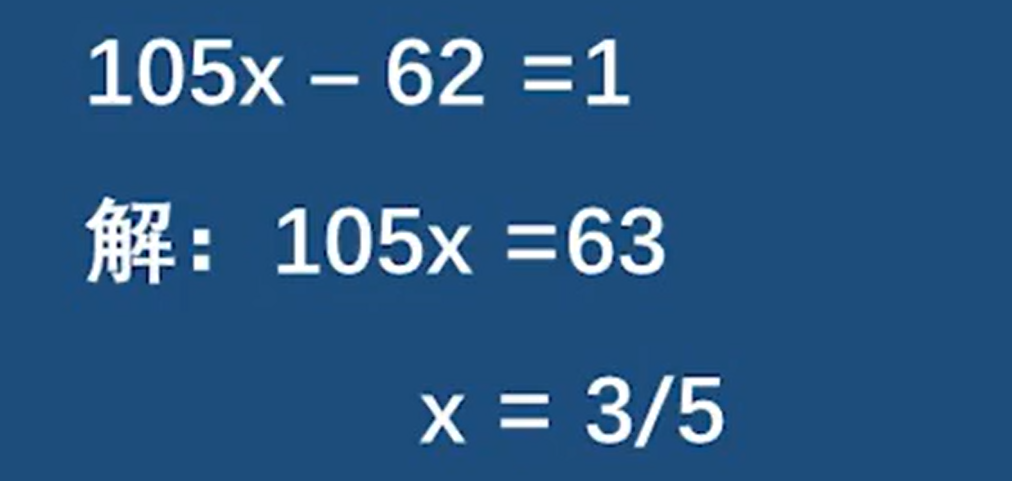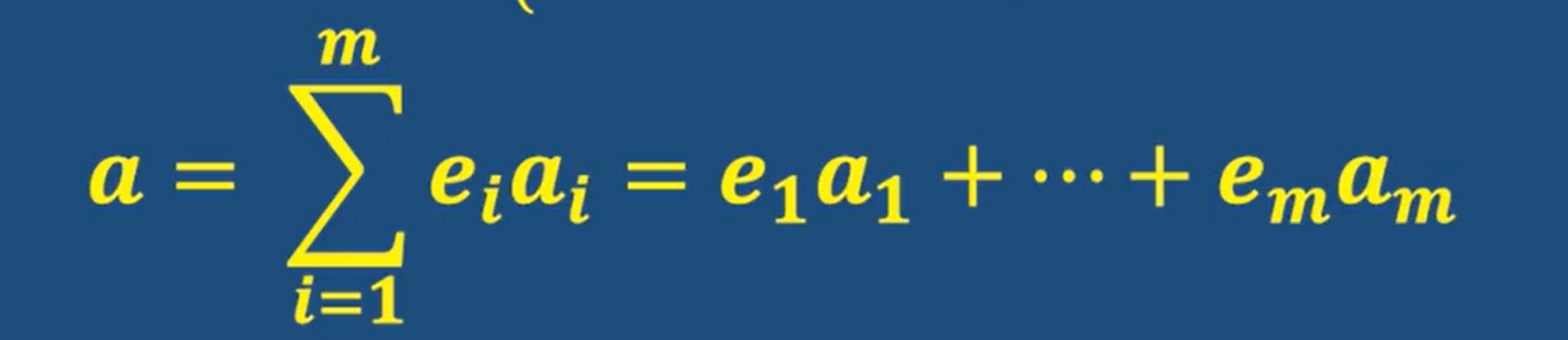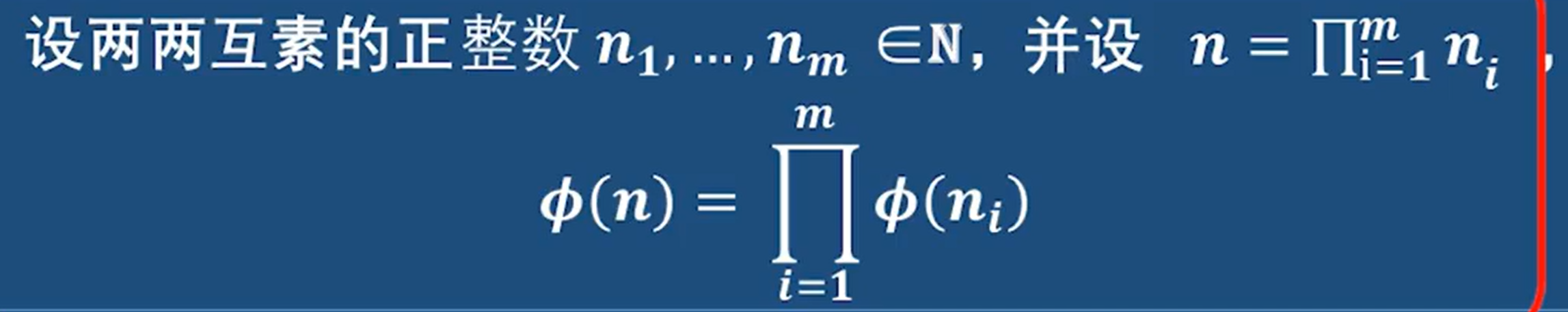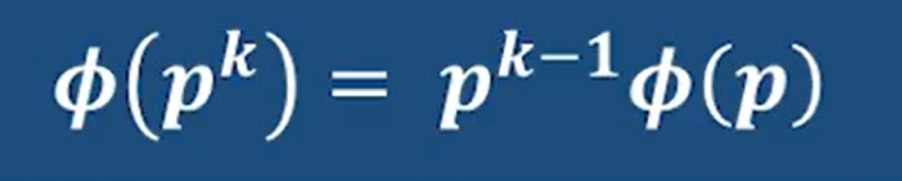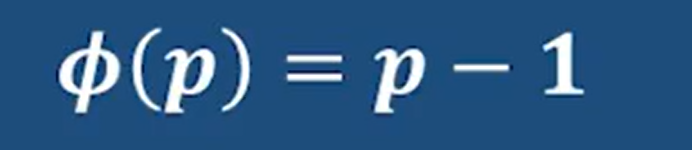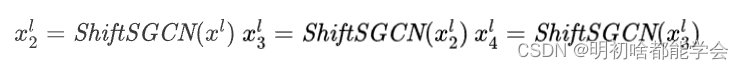数论基础
【专题说明】本系列文章主要根据B站Up主Alice-Bob学习数论基础知识,通过该系列文章,你可以对一些网安信安考试内容有一定了解,同时对于CTF中密码学方向的赛题在数论部分有更深的理解,如有不当之处,师傅们及时批评指正!
【专题展望】该系列文章会持续更新,同时后面后选择一些相关考点的CTF赛题进行补充讲解记录,毕竟学到的知识用起来才是自己的嘛!
文章目录
- 数论基础
- 0导读
- 1-1 整除*
- 1-2 素数*
- 1-3 模运算*
- 1-4 最大公约数*
- 1-5 扩展欧几里得算法*
- 1-6 最小公倍数*
- 1-7 证明算术基本定理*
- 1-8 等价关系
- 1-9 同余*
- 1-10 乘法逆元
- 1-11 一次同余方程*
- 1-12 剩余类*
- 1-13 中国剩余定理
- 1-14 欧拉函数*
- 1-15 欧拉定理、费马小定理*
0导读
0不是自然数
抽象代数 => 主要研究代数结构 就是离散数学中的群、环、域、格
标题带星号* 表示专业课程内容涉及
1-1 整除*
整除性(Divisibility)

性质:

解释:
:happy: 任何整数都是0的因子
:happy: 1是任何整数的因子
:happy: 这个地方存在一个争议 就是b不能为0的问题 注意一下就好
:happy: 如果b是a的因子,那么b也是-a的因子 -b也是a的因子 人话就是因子关系与正负无关
性质:

注意:
消去律中c不能为0
比较重要的时线性性:
如果b是a和c的因子,对于所有整数 都存在b是a和c线性组合后的因子
讲解一下如何证明:
对于整除的一些证明,一般都转化为等式 如b | a <=> a = qb
定理:

将b设为1 直接得到第二部分结论
特别符号

课后练习:

证明:

b就是所有ai的和
1-2 素数*
Prime
定义:正整数n >=2 除了1和n以外,没有其他正整数整除n 此时n称为“素数”;否则n称为“合数"
ps: 1既不是素数,也不是合数
ps:若n为合数,则n = ab 1< a <n 1< b <n
引理2-1:任何大于1的整数必有素因子
理解:大于1的整数不是素数就是合数,对于素数,其本身就是自己的素因子,所以必然存在;难点在于合数,即说明合数(必然大于1)一定存在素因子
证明:存在必有,一般考虑反证法
既然上面可知任何合数都一定存在素因子,那么素因子的范围是多少
定理2-1:任何合数n都至少有一个不超过 n \sqrt n n 的素因子
证明:存在至少,浓浓的反证味
应用:
判断n是否是素数:如果所有素数 p < = n p <= \sqrt n p<=n 都不能整除n,则n是素数(缩短穷举的范围 仅对小整数适用 在密码学中 大素数效率非常低
举例:
定理2-2:算术基本定理

ps:
用法:下一个定理
定理2-3:欧几里得定理(Euclid’s Theorem):素数有无穷多个
证明:反证法
1-3 模运算*
密码学中非常重要的一个运算,一定要理解其性质和运算方法
形式:

负数求模:
举个🌰:-13 mod 7 = 1
计算小窍门:-13 不断加7 直到为正数, 正数是几,答案就是几
-13 + 7 = -6 + 7 = 1
归纳一下 2 * 7 -13 = 1
利用数轴法进行巧算:
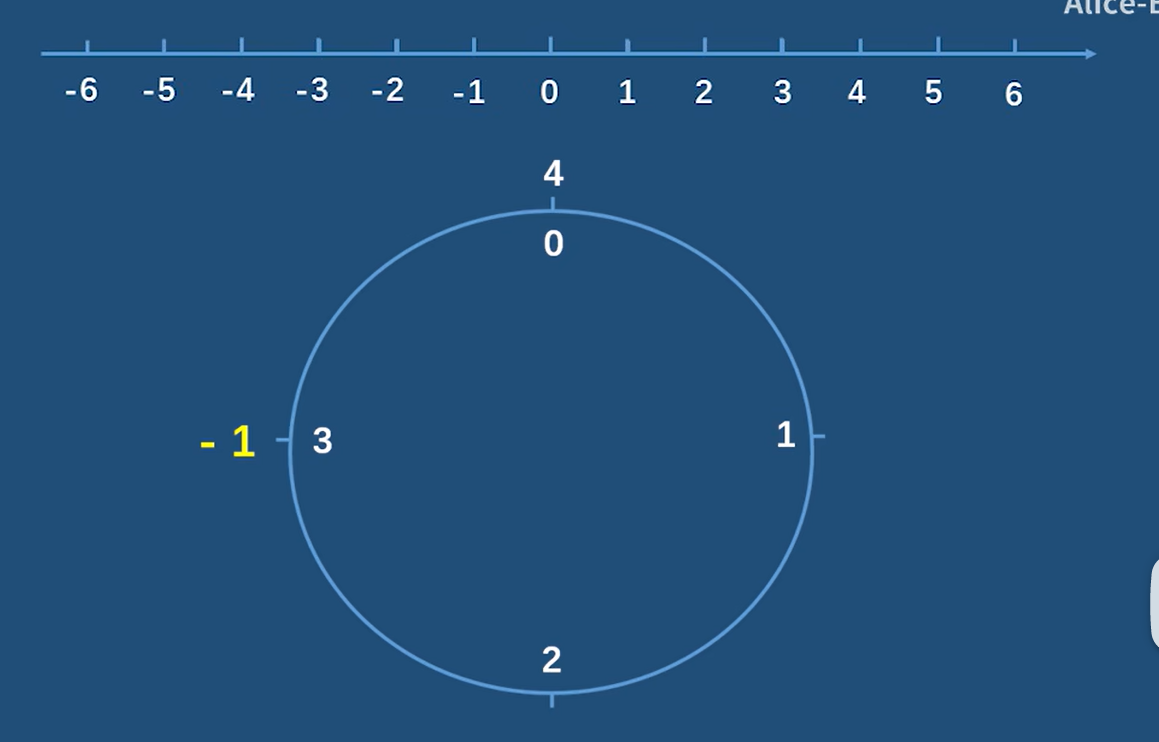
当模数是4 则将0-3卷成一个钟表
-1 mod 4 = 3
-5 mod 4 = 3
性质:
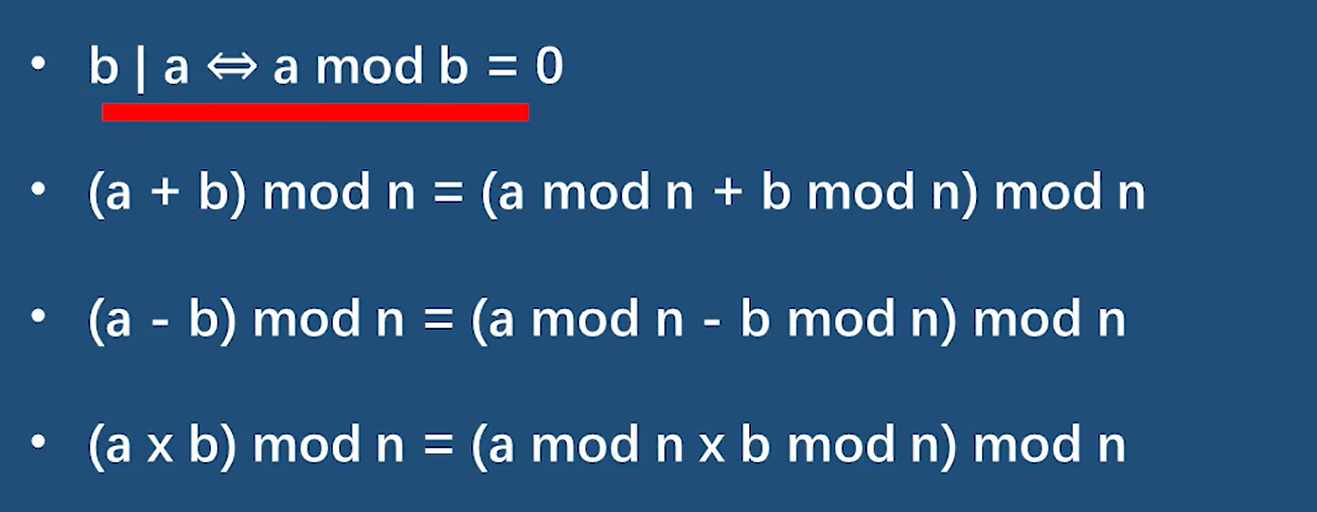
举例:
应用:
每一步计算都可以模模数以化简中间结果
注意!最后一步一定要模5!
除法没有这样的性质
1-4 最大公约数*
定义:

解释:所有公因子整除d
即为d = q*公因子
ps:
此外gcd(0,0) = 0
举例:直接转化为正数
互素:


证明:
举例:
上面这个q1和q2就是互素的 gcd(q1, q2) = 1
那么已知两个数 如何求最大公约数呢, 欧几里得算法!也称为辗转相除法
欧几里得算法(Euclid’s algorithm)
不失一般性,设a >= b >= 0, 求gcd(a, b)
数学原理:
b = 0时,gcd(a, 0) = a (因为任何整数都是0的公因子)
b > 0时,gcd(a, b) = gcd(b, r) 其中关系为:a = qb + r (因为如果d是b和r的公因子 则一定是a的公因子 可提取)
举例
1-5 扩展欧几里得算法*
定理5-1 最大公约数表示定理:设a, b属于Z, d = gcd(a, b), 则存在s,t 属于Z 使得as + bt = d
翻译成人话就是 整数a和b的因子 和a和b一定存在线性关系
特别的,当a和b互素即gcd(a, b) = 1 则as + bt = 1
人话就是没什么区别 只不过这里d = 1
推论:d | v <=> as + bt = v
解释:去回忆整除 这里d是v的一个因子 右边a和b的最大公因子是v 则d也是其因子
基于上述定理 得到扩展的欧几里得算法 也叫广义欧几里得算法
用途:计算as + bt = gcd(a, b) 中的s和t
既然是扩展欧几里得算法,那么一定跟欧几里得算法有关系啦
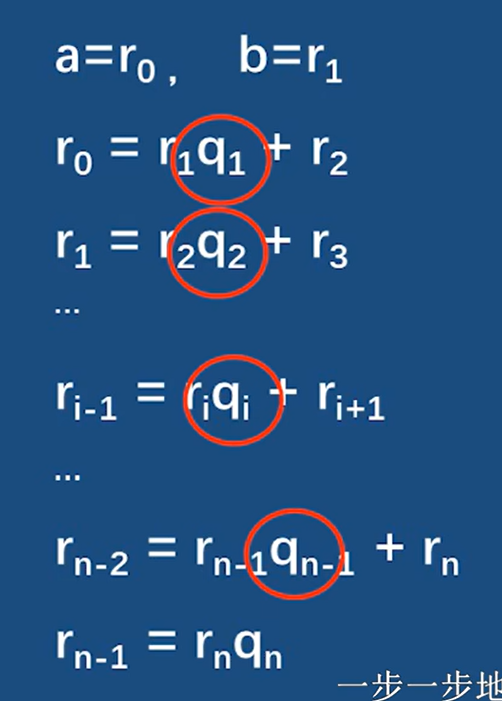
这里是求gcd(a, b) = rn
在应用欧几里得算法的过程中 其实q是没有用的 但是在扩展欧几里得中 我们需要理由q
求法:先假设
然后利用归纳法进行证明推导
进一步
则s和t 就是sn和tn
应用:
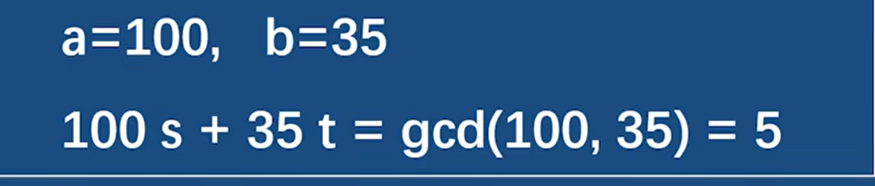
计算:
第一步拆:100 / 35 = 2 … 30
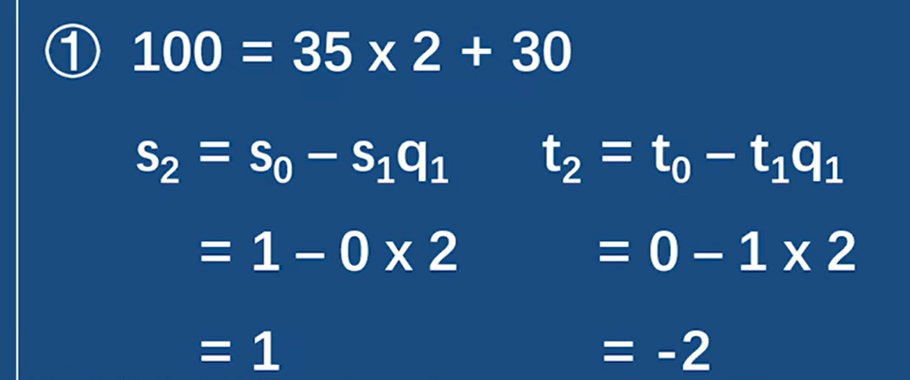
第二步 辗转相除 35 / 30 = 1 … 5
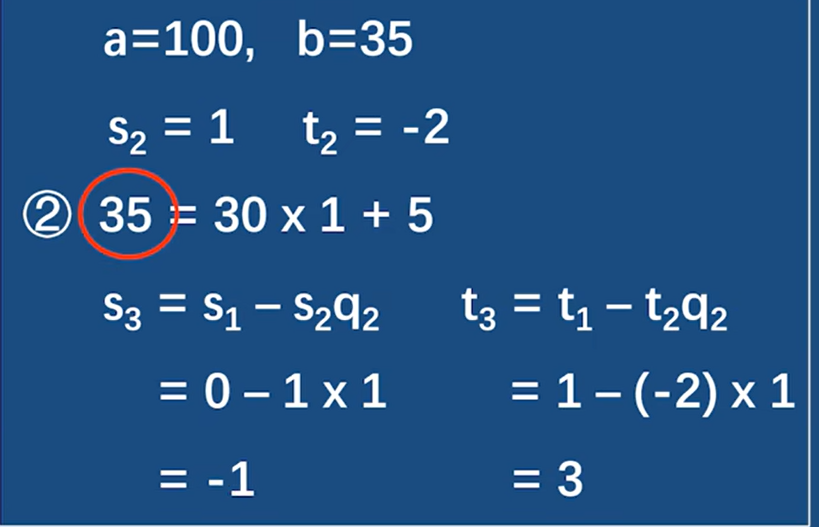
第三步 30 / 5 = 6 … 0 余数为0 停止 被除数为结果

最终直接结束
在python中存在该函数库直接调用
g,s,t = gmpy2.gcdext(e1,e2)
1-6 最小公倍数*
先解释一下什么是公倍数:
a和b都是整数,如果m(整数)分别是a和b的倍数,则m是a和b的公倍数 可以为负哦~
然后是最小公倍数:

推论:
- 设m = lcm(a, b) 如果a | c, b | c, 则 m | c
- 若gcd(a, b) = 1 => lcm(a, b) = ab 举例 3和5 最小公倍数就是15
计算公式:lcm(a, b) = ab / gcd(a, b)
上面这个用到了一些乘乘除除 但是我们知道在计算机中乘法效率较慢,所以尝试使用加法求解lcm
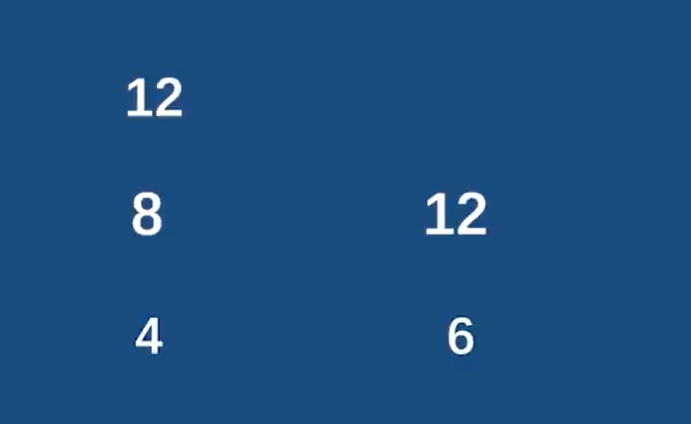
原理:两数中小的加自己,然后进行比较,直到两边相等
举例:
1-7 证明算术基本定理*
算数基本定理:任何非零整数n,可以表示成下面的乘积形式
证明存在性:

证明唯一性:
首先引入一个小定理:
设p是素数,a和b是整数,则p | ab => p | a 或 p | b
翻译成人话,因为p是素数,所以如果p是a乘b的因子 则p是a或b的因子
推论:设p是素数,
举例:
唯一性证明:

1-8 等价关系
两个关联点:集合、二元关系
主要涉及三种关系:自反性、对称性、传递性
举例1:

人话:
- 3=3
- 3=3 => 3=3
- 3=3 3=3 => 3=3
举例2:

人话:
- 三角形与自身全等
- 三角形A与三角形B全等 则 三角形B也与三角形A全等
- 三角形A和B全等 B和C全等 则三角形A和C全等
举例3:

反例1:

反例2:

给出正式定义:(集合的表示方法)

抽象表示:(类似二元运算的表示方法)

1-9 同余*
基本概念:

注意一下含义:同余之所以叫同余关系,是因为其表示的是一种关系而不是运算
区分:

正式定义:

解释说明:
因为(a - b)整除n 所以r1-r2必然为0 即r1 = r2 则表示同余
性质: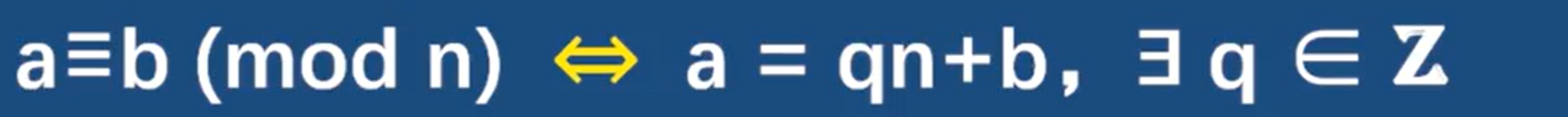
证明:对b的式子进行变形 然后带入到a中

稍微一变形:a - b = qn 你想到了什么, 正是上面的n | (a - b)
一点说明:同余是一种等价关系,如果忘记了等价关系看上一章,那么等价关系具有的一切性质,同余也都具有
运算性质:
因为同余,所以加减乘三种运算和整数中没有任何区别
对自身的操作:

两式之间的操作
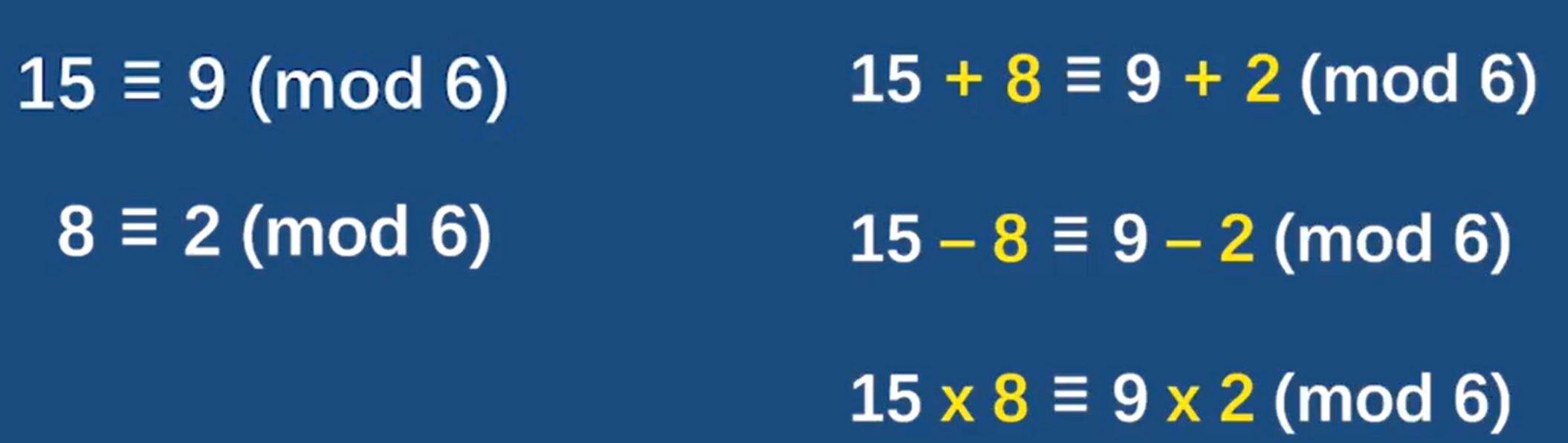
注意嗷!必须是同余!! 上面这两个式子就是对mod 6同余
1-10 乘法逆元
乘法逆元 说的就是我们上面同余式中的除法运算,相比于普通整数中的除法还是有一点点区别滴
引入,先来一个普通乘法:
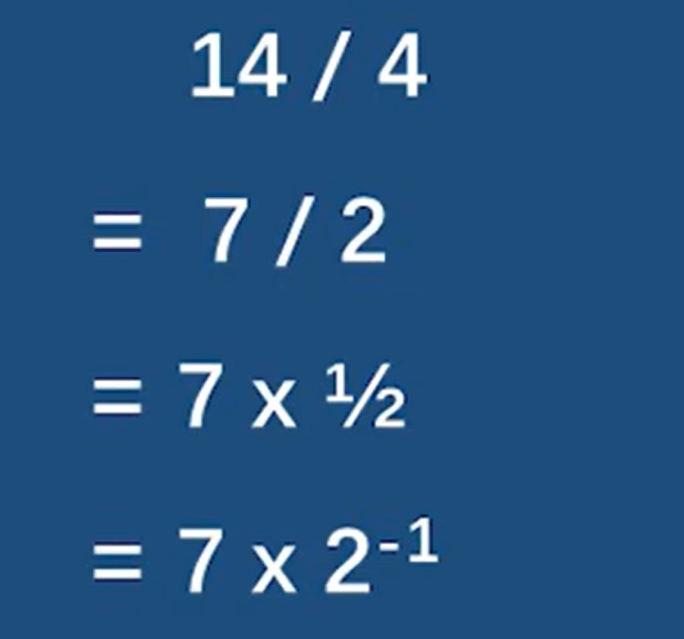
加入同余:

打起精神:这里的操作都是可以的!by the way 这不是最终答案!
因为在模运算下最终的结果一定是一个整数,也就意味着 2 − 1 2^{-1} 2−1 是一个整数 显然是有点问题的 所以需要转化为一个整数 下面继续看乘法逆元 看一下在mod 5的情况下 2 − 1 2^{-1} 2−1能转化为哪个整数
在乘法逆元中:
先回顾一下倒数的概念:两个数的乘积为1,就称这两个数互为倒数
那么在同余中 就是两数相乘取余的结果为1 就乘为倒数
那么上面中
2
−
1
2^{-1}
2−1 表示2在模5下的倒数
2
×
3
m
o
d
5
=
1
2 \times 3~mod~5 = 1
2×3 mod 5=1
故转化为3

举例:相同的数 在不同的模数下 其乘法逆元也不同

在计算过程中,我们通过第一个例子也可以看出 很多其实仍然继承了幂运算中的性质 只有在-1次方表示倒数的时候用到了mod的数值

定义:

注意点:
- 模n下互为乘法逆元,一般只考虑比n小的
- 模n内的乘法逆元是唯一的
- by the way 有的时候整数会以自身为乘法逆元 比如1 模任何下都是1本身 再比如4 mod 5 4就是4本身的乘法逆元
- 乘法逆元的存在条件:!!!!!!
举例 在mod 4下 2没有逆元 所以条件为 整数和模数必须互素
证明:在最后d | 1 则表明d=1 但是我们假设d不等1 而是大于1
乘法逆元的求法!蛮重要的,可以设个考点:

既然得知s就是模n下的逆元,所以调用一下扩展欧几里得算法 一计算 返回的s 就是答案
1-11 一次同余方程*
在上面了解了乘法逆元之后,我们就可以在同余的情况下进行解方程啦
原理引入:
没有模数下的为一次方程非常普通,下面给这个方程加点料,加一个模数
到此引出一次同余方程的样子,加减乘都好办,就是除法比较特殊,下面先给出一点小demo
首先看一个典型错误:
可以发现最后3和1在模6下同余,但这个根本是错的,那我们把后面的式子展开一下,找一找问题出在哪
问题就在我们没有对mod 6同时做除法,即为:
这里需要观察,我们上面的那个之所以需要对模数进行除法,因为3和6不互素 即gcd(3,6)=3
如果需要除的数和模数互素,则不需要对模数进行操作,如下:因为此时乘法逆元存在
再来个例子:

首先105和63有最大公因数21 但是不能直接除21 因为gcd(21,6) = 3 需要对模数操作
分两步走,21->3,7 因为gcd(3,6)=3 所以不能直接除3 而应该对模数也操作
对于7 gcd(7,2)=1 互素, 所以模数没有影响
但两步走有些麻烦啊,怎么化简一下嘞:
因为gcd(105,63)=21
所以直接除21 对于模数的操作为除21和6的最大公因数 gcd(21,6)=3
到此引出消去律

到此开头的一次同余方程可解

解释一下最后几步,3/5 相当于3乘5在模2下的逆元 即考虑谁乘5mod2 =1 即答案一定小于模数 故为1
即x与3mod2同余 进一步处理 将答案放到模数下 即x与1mod2同余
最终答案只有1吗 绝对不是!而是一个剩余类 1 + 2k都可以!通式如下:
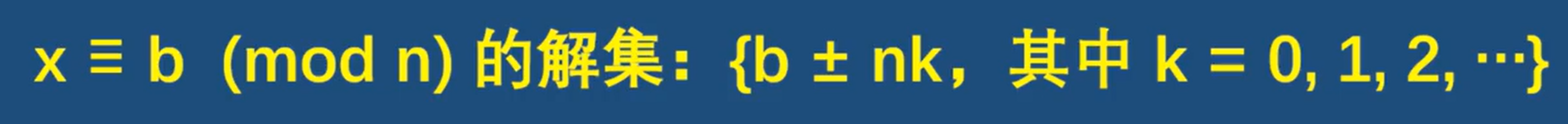
解后拓展:观察方程

模数缩小了三倍 在解集中0-5 6个数之间 解的个数也为3,这也是规律嗷!

看一个无解的式子

下一步2要除过去了 但是gcd(2,6)= 2 两数不互素 需要对模数处理
即为 x = 3/2 (mod 6/2) 即为 x = 3/2(mod 3)
这个时候处理分数 就是乘2在模3下的逆元 谁乘2 模3 = 1嘞 2本身! ????????我这个存疑 不理解哪错了
解释:不符合消去律 因为3里面没有2的因子
官方推理:因为gcd(2,6)=2 但是不存在2 | 3 故无解
在上面这个中 gcd(5,2)=1 互素 所以1 | 3始终成立 所以有解
有解的条件

1-12 剩余类*
前面的等价关系中 有=> 等价类
现在的同余关系中 有=> 剩余类
来个小栗子:

推广:

对比:

其实对比上面两个定义我们可以发现剩余类就是一种等价类
等价类的性质同样适用于剩余类的定义:

剩余类的记法:
如果该剩余类的余数为0 则即为[0]
代表元:剩余类中的每一个元素都是这个剩余类的代表元
剩余类集合:
注意上面这个剩余类集合,可以定义两种运算加法和乘法:

举例:


既然有乘法,那必然要考虑一下乘法逆元的问题

本质不变,只是形式略微有点变化

把这些存在逆元的剩余类放到一个新集合中

注意啊 若a=0 gcd(0,n)=n 因为0是任何整数的因子 所以最大公因子就是n本身
两者关系:

合数时表示真子集
最后来一个符号简化表示

给个demo
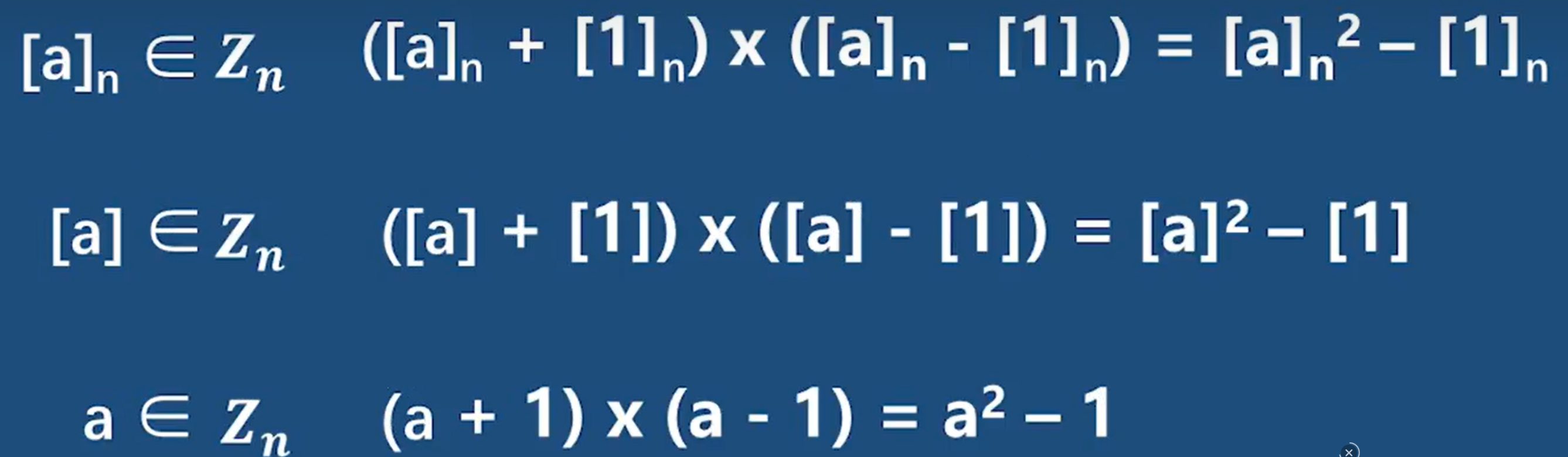
一定注意最后的a和1都是剩余类而不是整数
1-13 中国剩余定理
上一节学会了求解一次同余方程
但是我们小学学完方程学的是什么,正是方程组
所以下面我们通过中国剩余定理CRT(Chinese remainder theorem) 去求解一次同余方程组
先看看一次同余方程组的样子吧:

注意前提条件:模数必须两类互素
在CRT中告诉我们上面这个式子必有解

下面重点介绍如何使用CRT进行计算:
首先对每个n进行操作:
这个很好理解啊,因为n1*中去掉了n1本身 然后其他的都两两互素 所以n1*和n1一定也互素嘞
既然都互素,则存在一定存在乘法逆元,都记为t
把这个式子汇总一下为:
之所以第二个为0 是因为ni*中没有ni 但是有nj 所以模为0
此时就可以得到方程组的一个解了 注意这个解就是x 只不过我们先用a表示 不过那些ai 却是式子中的a1 - am
此时 去思考一个点哈:
那就是a模ni 得到的余数就是ai,原因在于因为e的原因 当模ni的时候,存在ni的都会为0 所以此时只剩下eiai 然后又因为ei与1模ni同余 所以最终只有ai
OK 最后收尾总结:里面的ni*-1 是ni*在模ni下的乘法逆元 也就是上面的ti 一回事 别慌
在模1以内有唯一的解,即a mod n
下面给出应用实例:

解题:a1 = 2 a2 = 3 a3 = 2 n1 = 3 n2 = 5 n3 = 7
n = 3 × 5 × 7 = 105 n 1 ∗ = n / n 1 = 35 逆元: 35 在模 3 的逆元为 2 n 2 ∗ = n / n 2 = 21 逆元: 21 在模 5 的逆元为 1 n 3 ∗ = n / n 3 = 15 逆元: 15 在模 7 的逆元为 1 a = 35 × 2 × 2 + 21 × 3 × 1 + 15 × 2 × 1 = 233 最终答案 a m o d n = 233 m o d 105 = 23 n = 3\times5\times7=105 \\ n_1^* = n / n1 = 35~~~~逆元:35在模3的逆元为2 \\ n_2^* = n / n2 = 21~~~~逆元:21在模5的逆元为1 \\ n_3^* = n / n3 = 15~~~~逆元:15在模7的逆元为1 \\ a=35\times2\times2+21\times3\times1+15\times2\times1 =233 \\最终答案a~mod~n = 233~mod~105=23 n=3×5×7=105n1∗=n/n1=35 逆元:35在模3的逆元为2n2∗=n/n2=21 逆元:21在模5的逆元为1n3∗=n/n3=15 逆元:15在模7的逆元为1a=35×2×2+21×3×1+15×2×1=233最终答案a mod n=233 mod 105=23
占个坑吧:双射关系 不理解
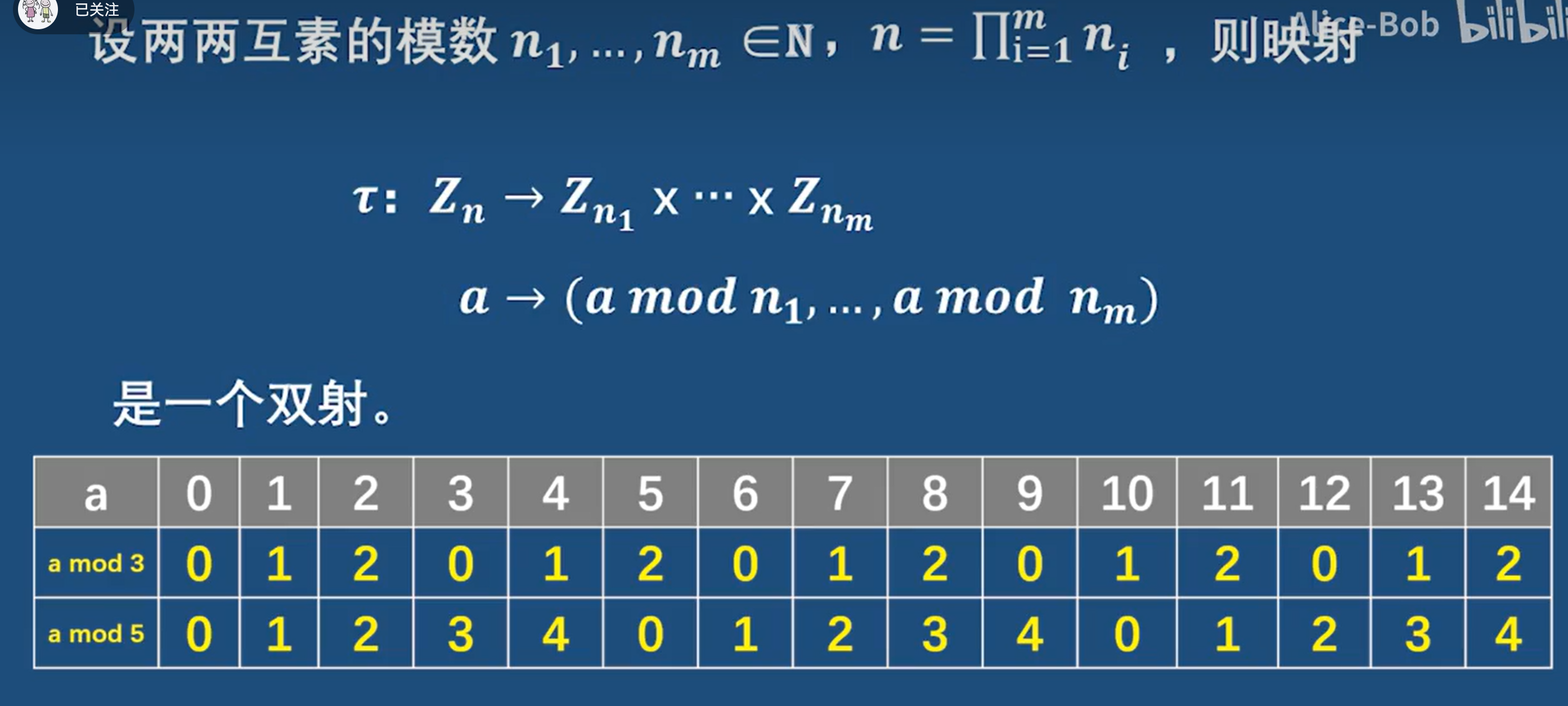
1-14 欧拉函数*
首先先回顾一个符号

Zn* 中整数是谁不是我们这节关注的,而是要关注Zn* 中整数的个数,这个个数也就是欧拉函数记作
ϕ
(
n
)
\phi(n)
ϕ(n)
给出定义:

即0到n-1之间与n互素的整数的个数
举个例子:

还是要记得gcd(0,n)=n 这也就是为什么phi(1) = 1 因为gcd(0,1)= 1
小点的数我们还可以这样列出来数一数
但是n一旦比较大,我们就需要借助欧拉函数的运算性质啦
注意啊 这里的p表示素数 只有素数才适用 非素数有其他计算法
这里推导一下2和3
举个例子吧
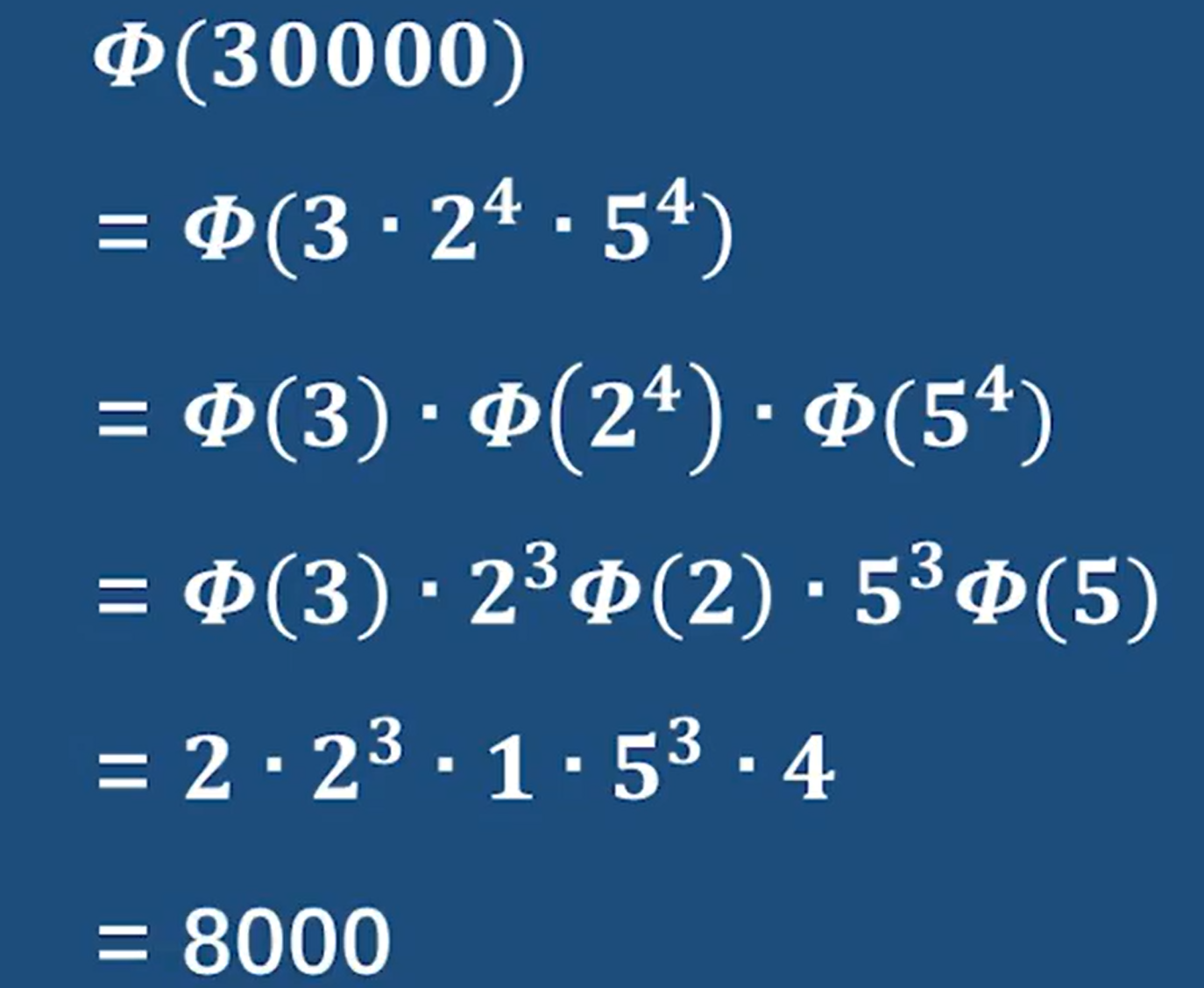
1-15 欧拉定理、费马小定理*
首先还是先引入一个新的概念
- 乘法阶:

- 性质:

证明:

因为a属于Zn* 所以与n互素 所以两边同除不需要改变模数n
所以推导出最终的结果t < k与k是n的阶相矛盾
由此得出性质:

举例:一定要先知道阶为多少 但是这有些麻烦啊

那么像不需要知道阶进行化简,下面引出重点:
- 欧拉定理:应用前提a和n之间必须互素

化简:
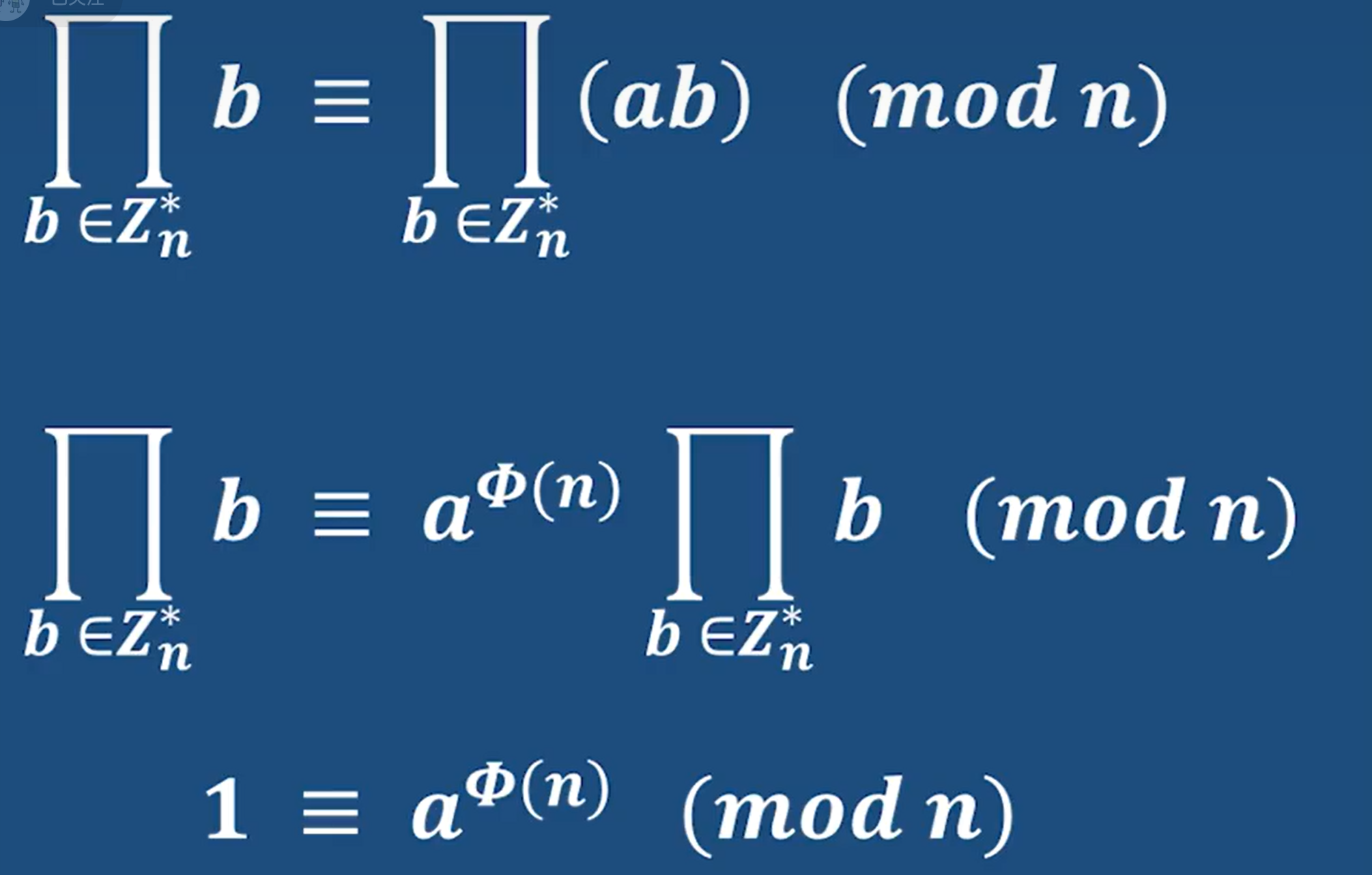
一道非常好的例题,融合前面知识:

下面开始推导费马小定理
首先要说的,费马小定理其实就是欧拉函数的一种特殊情况
把模数n限定到素数p表示

然后两边同时乘a
得到

最后是一个关于乘法阶的计算问题


补充定理: