第二章 关系数据库

2.1 关系数据结构

2.1.1关系

关系模型的数据结构十分简单，只包含单一的数据结构——关系。在用户看来，关系模型中数据的逻辑结构是一张扁平的二维表。关系模型的数据结构虽然简单却能表达丰富的语义。在关系模型中，现实世界的实体以及实体之间的联机都是用单一的关系结构类型来表示。

1.域（domain）
定义：域是一组具有相同数据类型的值的集合。例如学生数据库中所有的学生名字，或者性别的取值只有男或女，这就是性别的域

2.笛卡尔积
在一组域D₁,D₂,D₃…D_n中的笛卡尔积是：D₁xD₂xD₃…D_n 。其中每一个元素(d₁,d₂,d₃,…d_n)称为一个n元组，元素中每一个d_i称之为一个分量一个域允许的不同取址的个数称为这个域的基数。笛卡尔积可以表示为一个二位表，表中的每一列来自一个域。比如给出三个域：

则D1、D2、D3的笛卡尔积为

这些笛卡尔积可以制作成一张二维表，如图

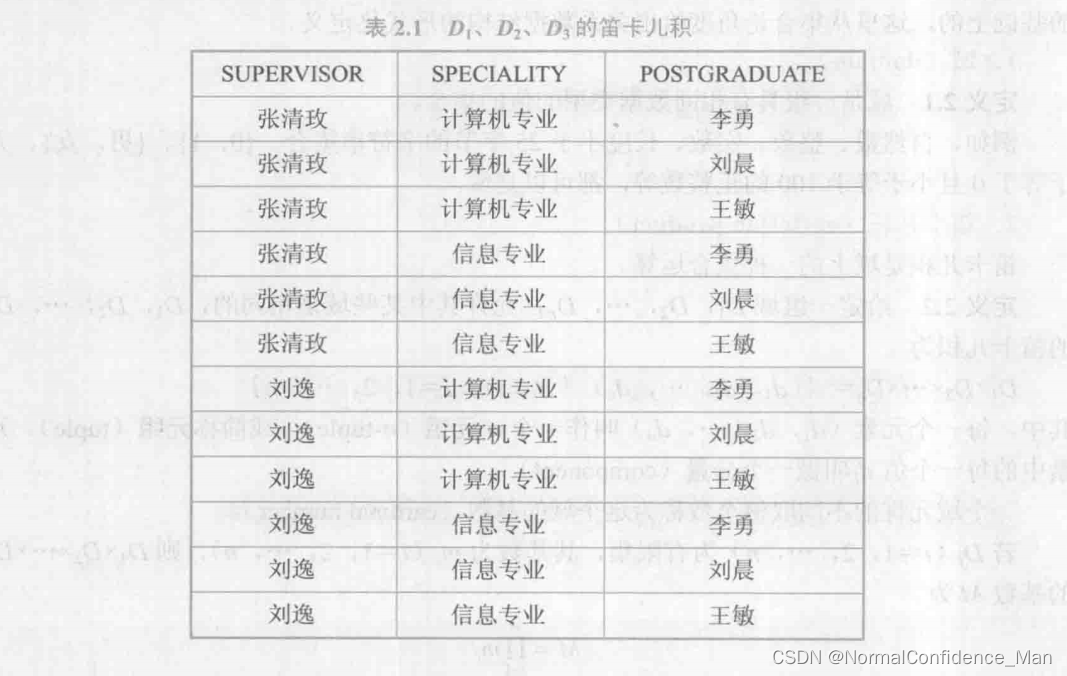
3.关系

D₁xD₂xD₃x…xD_n的子集叫做在域D₁,D₂,D₃…D_n上的关系，表示为R(D₁,D₂,D₃…D_n)，R表示关系的名字，n是关系的目和度。比如一个实体：学生（学号，姓名，班级，院系），其中R为学生，n为4

关系中每个元素是关系中的元组，使用t来表示。关系是笛卡尔积的有限子集，表的每一行对应一个元组，表的每一列对应一个域。由于域可以相同，为了区分，必须给每一列起一个名字，称之为属性。n目关系有n个属性。

如果关系中某一属性的值能够唯一的标识一个元组，而其子集不能，则称该属性组为候选码（比如学生表中的学号，通过学号可以确定是哪个学生，但是靠班级或者性别是不行的）。如果一个关系中有多个候选码，则可以选择其中一个作为主码(primary key)。候选码的各个属性称为主属性。不包含在任何候选码中的属性称为非主属性。在最简单的情况下，关系模式所有的属性都是这个关系模式的候选码，称为全码

关系可以有三种类型：基本关系、查询表和视图表。基本关系就是实际存在的表；查询表是查询结果对应的表；视图表是由基本表或其它视图表导出的表，是虚表，不对应实际存储的数据。

因此，基本关系具有一下六条性质：
（1）列是同质的，也就是每一列中的数据都是同一类型的来自同一个域的
（2）不同的列可能来自同一个域，称每个列为一个属性。比如学生的出生年份和入学年份两个不同的属性是来自同一个域的
（3）列的顺序无所谓，次序可以交换
（4）任意两个元组的候选慢不能取相同的值
（5）行的顺序也无所谓
（6）分量必须取原子值，每一个分量必须是不可分的数据项

关系模型中要求关系必须是规范化的，满足上述条件的。规范化的关系简称为范式（Normal Form,NF)

2.1.2关系模式

关系是元组的集合，因此关系模式必须指出这个元组集合的结构。关系的描述称为关系模式，可表示为：

R(U,D,DOM,F)
R为关系名，U为组成该关系的属性名集合，D为U中属性来自的域，DOM为属性向域的映像集合，F为属性间数据的依赖关系集合。

2.1.3关系数据库

在一个给定的应用领域中，所有关系的集合构成一个关系数据库。

关系数据库的型又称为关系数据路模式，是对关系数据库的描述。关系数据库模式包含若干域的定义。

2.2 关系操作

2.2.1 基本的关系操作

常用的关系操作包括查询(query)、插入(insert)、删除(delete)和修改(update)。关系的查询表达能力强，查询的基本操作是选择(select)、投影(project)、连接(join)、除(divide)、并(union)、差(except)、交和笛卡尔积，这些在后面都会介绍。关系操作的特点是集合操作方式，就是操作的对象和结果都是集合。这部分会在后面详细介绍

2.2.2关系数据语言的分类

早期的关系操作能力通常用代数方式活着逻辑方式来表示，分别称为关系代数和关系演算。关系代数用对关系的运算来表达查询需求，关系元算则使用谓语来表达查询要求。另外还有一种介于关系代数和关系演算之间的结构化查询语言（SQL），具有丰富的查询功能，是集查询、数据定义和数据控制语言于一体的关系数据语言。我们的重点是在于学习SQL语言。

2.3 关系的完整性

关系模型中有三类完整性约束：实体完整性、参照完整性和用户定义的完整性

2.3.1 实体完整性

实体完整性规则：如果属性A是基本关系R的主属性（主键），则A不能取空值。比如学生（学号、姓名、专业号、班级号）这个表中学号为主码，则学号不可为空。

规则说明如下：

• 实体完整性规则是针对基本关系而言的，一个基本表通常对应现实世界的一个实体集合（比如学生表集合对应现实中的所有学生）
• 现实世界中的实体是可以区分的，也就是他们是具有某种唯一的标识的，录入每个学生都是独立的个体。相应的，关系模型中以主码为唯一性标识。
• 因此主码中的属性不能取空值，主码为空意味着该实体无法被唯一的标识，也就是该实体是无法被区分的。

也就是在学生表中，为了区分学生，必须要求作为主键的学号不能为空，如果学号为空，那么一旦出现重名的学生，就会无法区分两个学生，从而使得关系数据库出现逻辑错误。总之，实体完整性要求主键不能取空值。

2.3.2 参照完整性

现实世界之中实体之间往往存在某种联系，在关系模型中实体和实体之间的联系也是用关系来描述的。比如学生的班级号和班级表中的班级号是有联系的。因此定义了一种参考关系来说明实体和实体之间的联系，先看如下例子

比如有如下两个表：

学生（学号、姓名、班级号、专业号）
专业（专业号、专业名）

那么学生表的专业号信息均来自于专业表，那么学生表中就不可以出现专业表中不存在的专业。

定义：设F是基本关系R的一个或一组属性，但是不是R的主码，K是基本关系S的主码。如果F和K相对应，则称F是R的外码（Foreign Key），并且称R为参照关系，S为被参照关系或目标关系。

参照完整性规则是定义外码和主码之间的引用关系：
若属性或者属性组F是基本关系R的外码，他和基本关系S的主码K相对应，则对于R中每个元组在F上的只必须：

• 或者取空值（F中的每个属性值都是空值）
• 或者等于S中某个元组的主码值

回到刚才的两个表，其中学生表中的专业号和专业表中的专业号之间有外键关系：

学生（学号、姓名、班级号、专业号）
专业（专业号、专业名）

学生表中的“专业号”属性是参照专业表中的“专业号”的，那么可以有两种情况：

• 空值，表示还没有给学生分配专业
• 非空，但是值必须是专业表中存在的值
  也就是不可以出现不存在的专业号

2.3.3 用户定义的完整性

用户定义的完整性是针对某一具体关系数据库的约束条件，反应某一具体应用所涉及的数据必须满足语义要求。比如说规定学生成绩不可以有负数等等。在很早之前的关系数据库管理系统是没有提供定义和检验这些完整性的功能，所有都需要应用程序编写者负责，麻烦而且安全性不够高。

2.4 关系代数

关系代数是一种抽象的查询语言，他用对关系的运算来表达查询。关系代数的运算可以分为传统集合运算和专门的关系运算两种类型。其中传统的集合运算将关系看成元组的集合，其运算是从行角度进行的；而专门电费集合关系运算不仅涉及行，而且涉及列。

2.4.1 传统集合运算

传统集合运算是二目运算，包含并、交、差、笛卡尔积四种。我们设计两个表R和S举例子

1. 并集（Union）
   并集使用$\cup$表示，其中$R\cup S$表示R和S的并集，见图c。并集运算是将两个集合中出现的行组成一张新表，由属于R或属于S的行组成
2. 交集（intersection）
   交集使用$\cap$标识，其中$R\cap S$表示R和S的交集，见图d。交集运算是将两个集合中的公共行组合成一张新表，由既属于R又属于S的行组成
3. 差（expect）
   差集使用$-$表示，其中$R-S$表示R和S的差，见图e。差运算是提取属于R但不属于S的行
4. 笛卡尔积(cartesian product)
   $R\times S$表示R和S的笛卡尔积，如图f所示，R和S的笛卡尔积是一个n+m列的元素的集合。元素的前n列是关系R的一个元组，后m列是关系S的一个元组。

2.4.2 专门的关系运算

专门关系运算包括选择、投影、连接、除运算。

1.选择（Selection）

选择又称为限制，在关系R中选择满足给定条件的元组。比如说查询学生表中年龄大于20的学生

2.投影（Projection）

关系R上的投影上是从R中选择若干属性列组成新关系。比如在学生（学号，姓名，班级，专业）这个关系中，选择学号和姓名两列组成需变更呀必须。

3.连接（Join）

连接是从两个关系的笛卡尔积中选取属性之间满足一定条件的元组。连接分为等值连接、非等值连接和自然连接，其区别可以看下图，下图是对R中的B列和S中的B列进行等值、非等值和自然连接。其中：

1. 等值连接会从关系R和S的广义笛卡尔积中选取A、B属性值相等的元组。
2. 非等值连接则可以使用大于或等于进行连接。
3. 自然连接是一种特殊的等值连接，他要求两个关系中进行比较的分量必须是同名的属性组，并且在结果中将重复的属性列去掉。
   
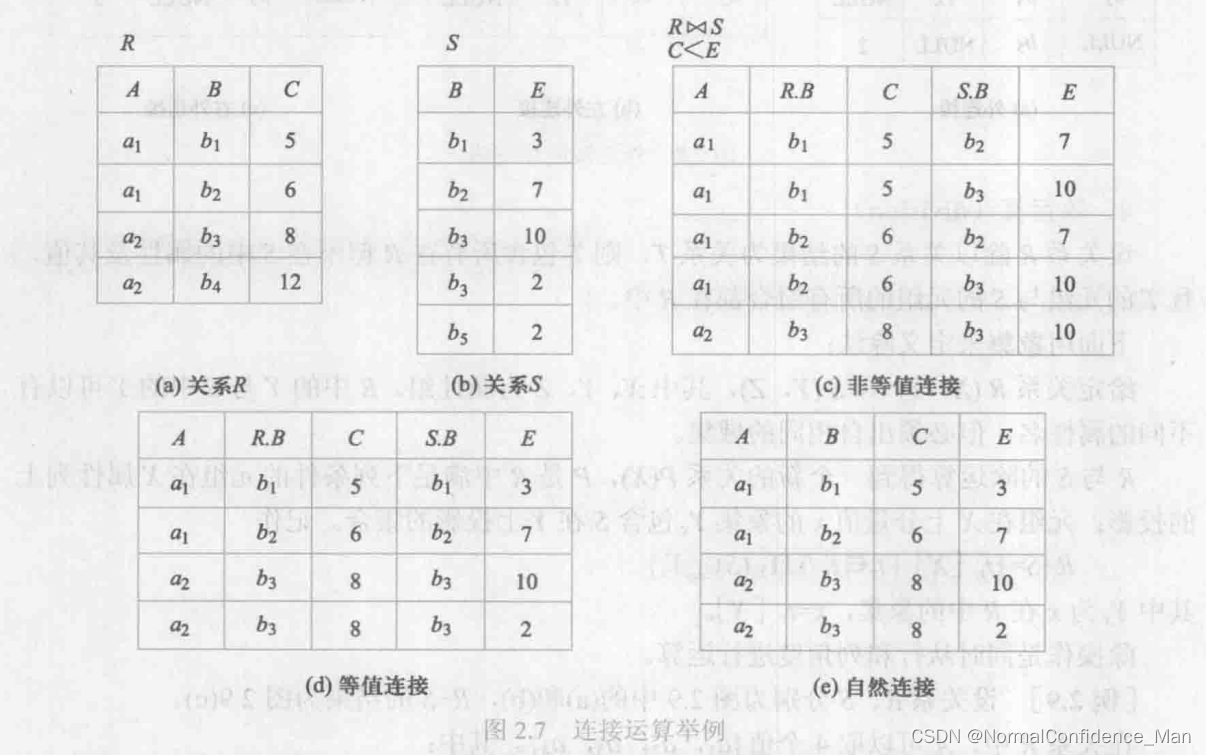
   两个关系R和S进行自然连接的时候，选择两个关系在公共属性上等值的元组构成新的关系。此时关系R中某些元组可能在S中不存在公共属性上相等的元组，从而造成R中这些元组被舍弃了，同样地，S中某些元组也会被舍弃。这些被舍弃的数组称为悬浮数组。

如果把悬浮数组也保存在结果关系中，而在其他属性上填上空值NULL，那么这种连接称之为外连接。在进行R join S的时候，只保留左边关系R中的悬浮数组称为左外连接（left join），只保留右边关系S中的悬浮数组称为右外连接（right join），如下图所示：

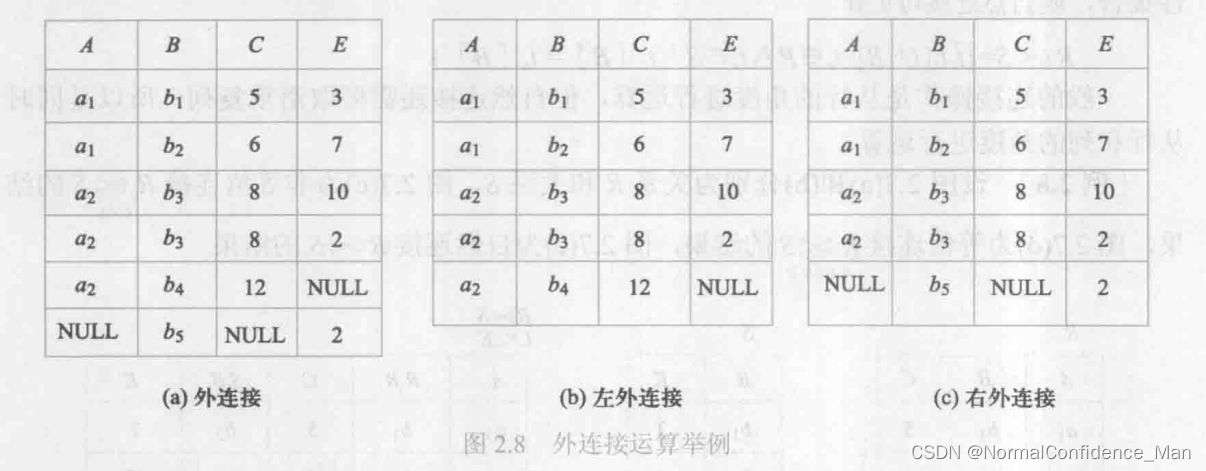
4.除运算（division）

设关系R除以关系S的结果为T，则T包含所有在R但是不在S中的属性以及其值，而且T的元组和S的元组的所有集合都在R中。