在此之前,可以先看看这篇二维数组之二维前缀和-首篇。
和为K的子数组
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。子数组是数组中元素的连续非空序列。
示例 1:
输入:nums = [1,1,1], k = 2
输出:2
示例 2:
输入:nums = [1,2,3], k = 3
输出:2
class Solution {
public int subarraySum(int[] nums, int k) {
Map<Integer, Integer> map = new HashMap<>();
int pre = 0;
map.put(pre, 1);
int ans = 0;
for(int i = 0;i < nums.length;i++){
pre += nums[i];
if(map.get(pre - k) != null){
ans += map.get(pre - k);
}
map.put(pre, map.getOrDefault(pre, 0) + 1);
}
return ans;
}
}
需要用到一维数组的前缀和。先给出一个示例数组和对应的前缀和数组。
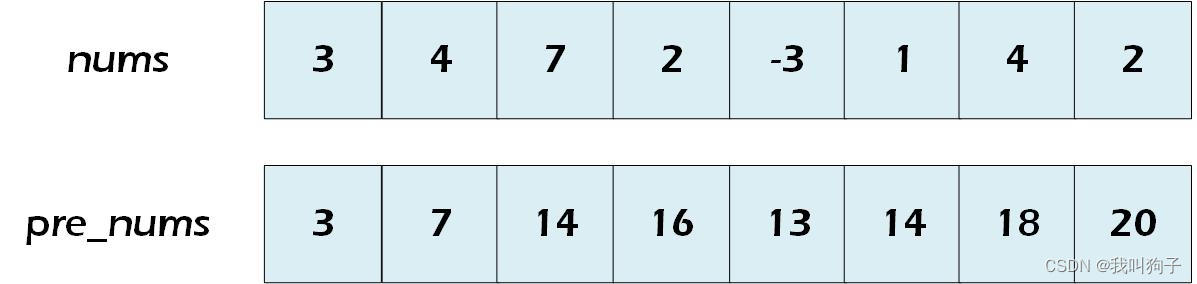
给定数组nums,和前缀数组pre_nums,如果子数组和为target(K),那么前缀和数组就需要满足pre_nums[j] - pre_nums[i] = target(K)。移项之后得,pre_nums[i] = pre_nums[j] - target(K)。也就是说,当得到一个前缀和为pre_nums[j]时,减去target(K),如果之前的前缀和中出现过pre_nums[i],说明从下标i到下标j的子数组满足和为target(K)。例如target为6,以上述图片中数组为例,pre_nums数组有一个前缀和为13,13 - target,也就是13 - 6 = 7,在13这个前缀和之前,有一个前缀和为7,说明从nums数组中从下标2到下标4的这段子数组的和为target,7 + 2 + (-3) = 6。
可以先计算前缀和,之后减去target(K),判断之前是否出现pre_nums[i],pre_nums[i]就是首元素到下标为i的元素的前缀和(i < j),所以需要保存之前元素的前缀和。要想较快的定位到对应pre_nums[i],可以用哈希表,key为前缀和,value为有多少个这样的前缀和,因为在下标j之前可能有多个值相同的前缀和,只是起始下标不同,但是都可以使得起始下标到下标j对应的子数组的和为target。
下面以图片示例为例,走一遍代码,设target(K)为7,首先将初始化前缀和pre等于0,这里不用使用数组来保存前缀和,因为已经使用哈希表对前缀和进行保存,所以只需要定义一个变量pre来保存当前首元素到当前元素的前缀和。map,put(pre, 1),意思就是前缀和为0的元素有1个。
之后进入for循环,首先pre += nums[0],等于3,3 - 7 = -4不在map中不进入if,map放入(3, 1)。此时map中有(0, 1),(3, 1)。
pre += nums[1],等于7,7 - 7等于0,所以说明[3, 4]这段子数组的和为target,由于初始化时将前缀和0放入在map中,进入if,ans += map.get(pre - k),ans += map.get(0),ans的值为1。此时map中有(0, 1),(3, 1),(7, 1)。
pre += nums[2],等于14,14 - 7等于7,说明[7]这个子数组的和为target。进入if,ans += map.get(7),ans等于2。此时map中有(0, 1),(3, 1),(7, 1),(14, 1)。
pre += nums[3],等于16,16 - 7 = 11,不在map中,此时map中有(0, 1),(3, 1),(7, 1),(14, 1),(16, 1)。
pre += nums[4],等于13,13 - 7等于6,不在map中,此时map中有(0, 1),(3, 1),(7, 1),(14, 1),(16, 1),(13,1)。
pre += nums[5],等于14,14 - 7等于7,在map中,且数量为1,ans += map.get(7)等于3。同时需要更新map中前缀和为14的value值为2。此时map中有(0, 1),(3, 1),(7, 1),(14, 2),(16, 1),(13,1)。
pre += nums[6],等于18,18 - 7等于11,不在map中,此时map中有(0, 1),(3, 1),(7, 1),(14, 2),(16, 1),(13,1),(18, 1)。
pre += nums[7],等于20,20 - 7等于13,在map中,ans += map.get(13),ans值为4。此时map中有(0, 1),(3, 1),(7, 1),(14, 2),(16, 1),(13,1),(18, 1),(20,1)。
for循环结束,返回ans等于4。
元素和为目标值的子矩阵数量
给出矩阵 matrix 和目标值 target,返回元素总和等于目标值的非空子矩阵的数量。
子矩阵 x1, y1, x2, y2 是满足 x1 <= x <= x2 且 y1 <= y <= y2 的所有单元 matrix[x][y] 的集合。
如果 (x1, y1, x2, y2) 和 (x1’, y1’, x2’, y2’) 两个子矩阵中部分坐标不同(如:x1 != x1’),那么这两个子矩阵也不同。
示例 1:
输入:matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
输出:4
解释:四个只含 0 的 1x1 子矩阵。
示例 2:
输入:matrix = [[1,-1],[-1,1]], target = 0
输出:5
解释:两个 1x2 子矩阵,加上两个 2x1 子矩阵,再加上一个 2x2 子矩阵。
示例 3:
输入:matrix = [[904]], target = 0
输出:0
class Solution {
public int numSubmatrixSumTarget(int[][] matrix, int target) {
int m = matrix.length;
int n = matrix[0].length;
int ans = 0;
for(int i = 0;i < m;i++){
int[] sum = new int[n];
for(int j = i;j < m;j++){
for(int k = 0;k < n;k++){
sum[k] += matrix[j][k];
}
ans += subarraySum(sum, target);
}
}
return ans;
}
private int subarraySum(int[] nums, int target){
Map<Integer, Integer> map = new HashMap<>();
map.put(0, 1);
int pre = 0;
int ans = 0;
for(int num : nums){
pre += num;
if(map.get(pre - target) != null){
ans += map.get(pre - target);
}
map.put(pre, map.getOrDefault(pre, 0) + 1);
}
return ans;
}
}
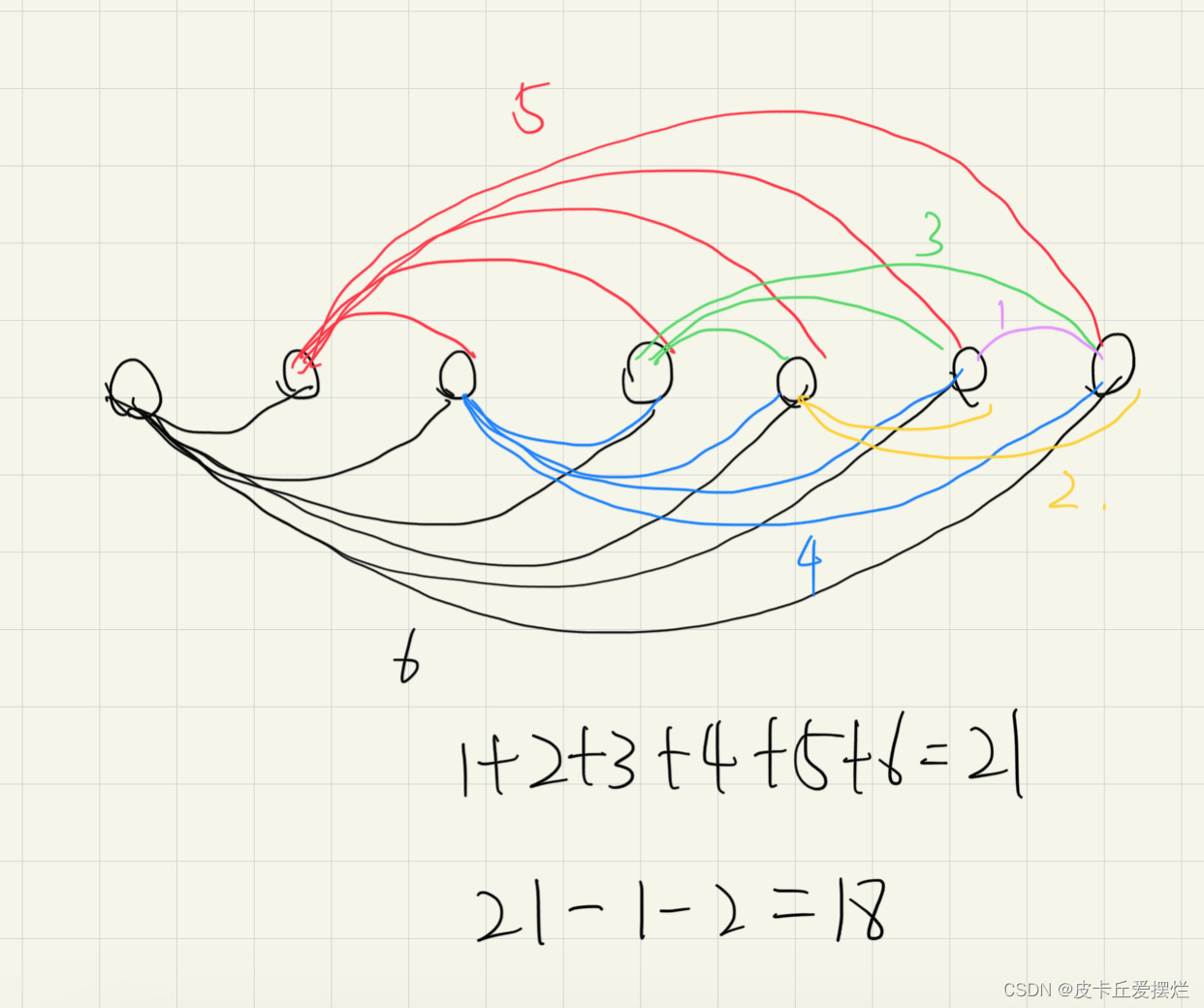
二维数组中元素和为目标值的子矩阵数量,就是将二维矩阵转化为一维矩阵,根据一维矩阵和为K的子数组的求解方法进行求解。那么现在的难点就是如果得到将二维矩阵转化为所有可能的一维矩阵。

如上图所示,按行遍历所有可能的行组合,有6种,之后分别计算这6种组合的列和用sum数组表示,这样就得到了一维数组,每个一维数组和为K的子数组数量之和就是二维数组中元素和为目标值的子矩阵数量。