Nim游戏
题目链接:Nim游戏
先说结论:假设n堆石子,石子数分别为a1,a2,a3.....,则当a1^a2^a3^...^an=0时先手必败,否则先手必胜。
因为所表示的二进制位必定是成对出现的,根据性质 1 ^ 1 = 0 ,0 ^ 0 = 0 得出结论。(具体证明过程不再说明)
因此代码如下:
#include <bits/stdc++.h>
using namespace std;
int n;
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
int ans=0;
for(int i=1;i<=n;i++){
int x;cin>>x;
ans^=x;
}
if(!ans)cout<<"No"<<"\n";
else cout<<"Yes"<<"\n";
return 0;
}台阶-Nim游戏
题目链接:台阶-Nim游戏
首先给出结论:所有奇数阶的石子个数异或,如果异或和为0,那么先手必败,否则先手必胜。
因为从第一阶拿下来石子要取1次,第二阶拿下来要取2次。。。。。以此类推,所以可以看成第二阶有两堆石子,第三阶有三堆石子,因为两堆相同数量的石子异或和必然为0,而奇数阶的石子异或和为本身,所以只需将奇数阶的石子异或计算即可。
#include <bits/stdc++.h>
using namespace std;
int n;
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
int ans=0;
for(int i=1;i<=n;i++){
int x;cin>>x;
if(i&1)ans^=x;
}
if(!ans)cout<<"No"<<"\n";
else cout<<"Yes"<<"\n";
return 0;
}集合-Nim游戏
题目链接:集合-Nim游戏
SG函数
这道题目用到了SG函数,那么首先介绍一下什么是SG函数以及用法:
首先定义MEX集合表示集合中最小的没有出现的自然数,如MEX{1,2}=0,MEX{0,1,2}=3.
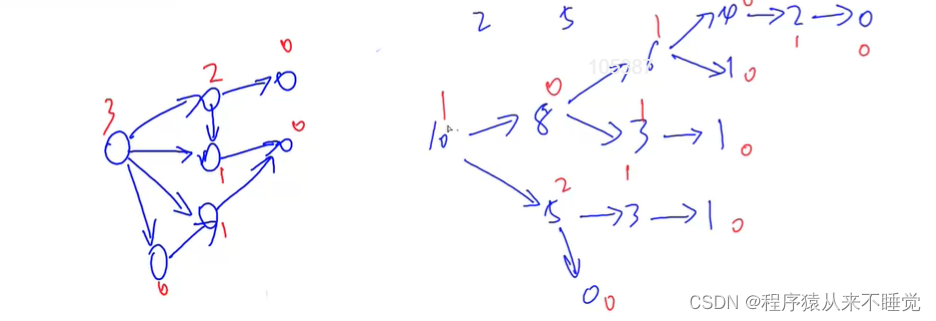
首先看左边这个图,我们把终点定义为sg(终点)=0;因为终点不能到达其他点,然后终点的前面一个点定义为sg(x)=1,因为后面有0,以此类推我们可以画出sg图。
那么SG函数具体的作用是什么呢?
首先终点的sg为0,意味着不能进行任何操作,在博弈论中意味着失败,那么当sg为0时,判负,相反,当sg不为0时,一定有一条路可以从该点走向sg(x)= 0,那么也就意味着如果先手不为0,那么一定可以让后手变为0.
接下来看题目,假设一堆有10个石子,我可以通过拿2个或5个使石子不能再拿,因此可以一个个枚举石子剩余的个数,如右图。接下来算出每个点的sg值,由图可知sg(10)=1,因此可以走到0让对手失败。
那么一堆是这样,n堆便用例题1的知识得:所有堆的sg异或和如果为0,先手必败,否则先手必胜。
#include <bits/stdc++.h>
using namespace std;
const int N =1e5+5;
int f[N],a[N];
int n,m;
int sg(int x){
if(f[x]!=-1)return f[x];//记忆化搜索
unordered_set<int>s;
for(int i=1;i<=m;i++){
if(x>=a[i]){
s.insert(sg(x-a[i]));
}
}
for(int i=0;;i++){
if(!s.count(i))return f[x]=i;
}
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
memset(f,-1,sizeof(f));
cin>>m;
for(int i=1;i<=m;i++){
cin>>a[i];
}
int ans=0;
cin>>n;
for(int i=1;i<=n;i++){
int x;cin>>x;
ans^=sg(x);
}
if(!ans)cout<<"No"<<"\n";
else cout<<"Yes"<<"\n";
return 0;
}拆分-Nim游戏
题目链接:拆分-Nim游戏
这道题目就是对sg函数的加深理解,sg函数有这样一个性质:
sg(b1, b2)=sg(b1)^sg(b2)
相当于一个局面拆分成了两个局面,由SG函数理论,多个独立局面的SG值,等于这些局面SG值的异或和。
可以类比上一道题目,根据sg函数的定义,每一个sg都能走到比自己小的每一个数。这和Nim游戏中的每一堆石子的性质相同,所以可以把每一个sg当成Nim游戏中的一堆石子,异或和就是总体局面的sg。
#include <bits/stdc++.h>
using namespace std;
const int N =105;
int a[N],f[N];
int n;
int sg(int x){
if(f[x]!=-1)return f[x];
unordered_set<int>s;
for(int i=0;i<x;i++){
for(int j=0;j<=i;j++){
s.insert(sg(i)^sg(j));
}
}
for(int i=0;;i++){
if(!s.count(i))return f[x]=i;
}
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
memset(f,-1,sizeof(f));
cin>>n;
int ans=0;
for(int i=1;i<=n;i++){
int x;cin>>x;
ans^=sg(x);
}
if(!ans)cout<<"No"<<"\n";
else cout<<"Yes"<<"\n";
return 0;
}