算法学习——LeetCode力扣补充篇11

64. 最小路径和
64. 最小路径和 - 力扣(LeetCode)
描述
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例
示例 1:
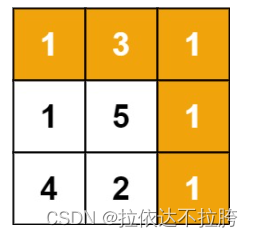
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 200
代码解析
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size() , n = grid[0].size();
vector<vector<int>> dp(m , vector<int>(n , 0) );
dp[0][0] = grid[0][0];
for(int i=1 ; i<m ;i++)
dp[i][0] = dp[i-1][0] + grid[i][0];
for(int j=1 ; j<n ;j++)
dp[0][j] = dp[0][j-1] + grid[0][j];
for(int i=1 ; i<m ;i++)
{
for(int j=1 ; j<n ; j++)
{
dp[i][j] = min( dp[i-1][j], dp[i][j-1] ) + grid[i][j];
}
}
return dp[m-1][n-1];
}
};
48. 旋转图像
48. 旋转图像 - 力扣(LeetCode)
描述
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例
示例 1:
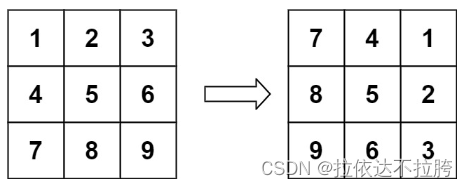
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:
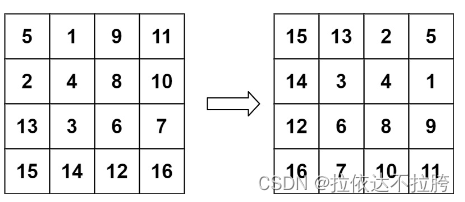
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示
n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000
代码解析
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
for(int i=0 ; i<m ; i++)
{
for(int j=i ; j<n ; j++)
{
swap(matrix[i][j] , matrix[j][i]);
}
}
for(int i=0 ; i<m ; i++)
{
for(int j=0 ; j<n/2 ; j++)
{
swap(matrix[i][j] , matrix[i][n-j-1]);
}
}
}
};
169. 多数元素
169. 多数元素 - 力扣(LeetCode)
描述
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例
示例 1:
输入:nums = [3,2,3]
输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2]
输出:2
提示
n == nums.length
1 <= n <= 5 * 104
-109 <= nums[i] <= 109
进阶:尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。
代码解析
class Solution {
public:
int majorityElement(vector<int>& nums) {
map<int,int> my_map;
pair<int,int> result(0,0);
for(int i=0 ; i<nums.size() ; i++)
{
my_map[nums[i]]++;
if(my_map[nums[i]] >= nums.size()/2)
{
if(my_map[nums[i]] > result.second)
{
result.first = nums[i];
result.second = my_map[nums[i]];
}
}
}
return result.first;
}
};
394. 字符串解码
394. 字符串解码 - 力扣(LeetCode)
描述
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
示例
示例 1:
输入:s = “3[a]2[bc]”
输出:“aaabcbc”
示例 2:
输入:s = “3[a2[c]]”
输出:“accaccacc”
示例 3:
输入:s = “2[abc]3[cd]ef”
输出:“abcabccdcdcdef”
示例 4:
输入:s = “abc3[cd]xyz”
输出:“abccdcdcdxyz”
提示
1 <= s.length <= 30
s 由小写英文字母、数字和方括号 ‘[]’ 组成
s 保证是一个 有效 的输入。
s 中所有整数的取值范围为 [1, 300]
代码解析
class Solution {
public:
string decodeString(string s) {
string res;
stack <int> nums;
stack <string> strs;
int num = 0;
for(int i = 0; i < s.size(); i++)
{
if(s[i] >= '0' && s[i] <= '9')
{
num = num * 10 + s[i] - '0';
}
else if(s[i] >= 'a' && s[i] <= 'z')
{
res += s[i];
}
else if(s[i] == '[') //将‘[’前的数字压入nums栈内, 字母字符串压入strs栈内
{
nums.push(num);
num = 0;
strs.push(res);
res.clear();
}
else //遇到‘]’时,操作与之相配的‘[’之间的字符,使用分配律
{
int times = nums.top();
nums.pop();
for(int j = 0; j < times; ++ j)
strs.top() += res;
res = strs.top(); //之后若还是字母,就会直接加到res之后,因为它们是同一级的运算
//若是左括号,res会被压入strs栈,作为上一层的运算
strs.pop();
}
}
return res;
}
};
240. 搜索二维矩阵 II
240. 搜索二维矩阵 II - 力扣(LeetCode)
描述
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
示例
示例 1:
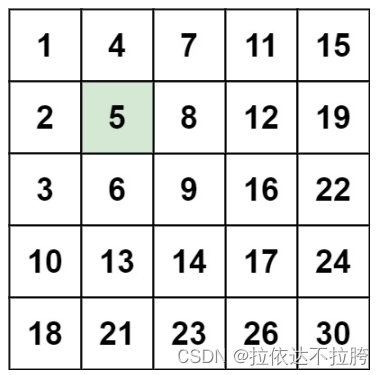
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true
示例 2:
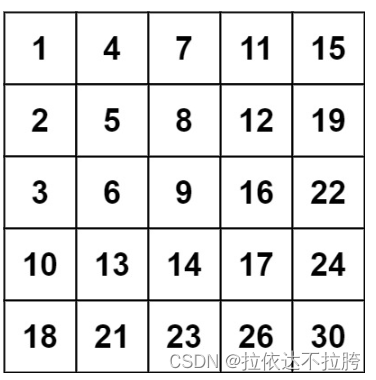
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出:false
提示
m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-109 <= matrix[i][j] <= 109
每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列
-109 <= target <= 109
代码解析
常规
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size() , n = matrix[0].size();
int max_point = 1;
for(int i=0 ; i<min(m,n) ;i++)
{
if(matrix[i][i] > target) break;
max_point = i;
}
for(int i=0 ; i < max_point ; i++)
{
for(int j=max_point ; j<n ; j++)
{
if(matrix[i][j] == target) return true;
}
}
for(int i=max_point ; i<m ; i++)
{
for(int j=0 ; j<n ; j++)
{
if(matrix[i][j] == target) return true;
}
}
return false;
}
};
路径优化
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size() , n = matrix[0].size();
int x = 0 , y = n-1;
while( x < m && y >= 0)
{
// cout<<matrix[x][y]<<endl;
if(matrix[x][y] == target) return true;
else if(matrix[x][y] > target) y--;
else if(matrix[x][y] < target) x++;
}
return false;
}
};