完全二叉树的节点个数
leetcode : https://leetcode.cn/problems/count-complete-tree-nodes/
递归思路
递归的思路很简单, 假设们要统计一棵树的节点数, 那么 只要统计根节点的左子树的节点数, 和右子树的节点数加上根节点即可
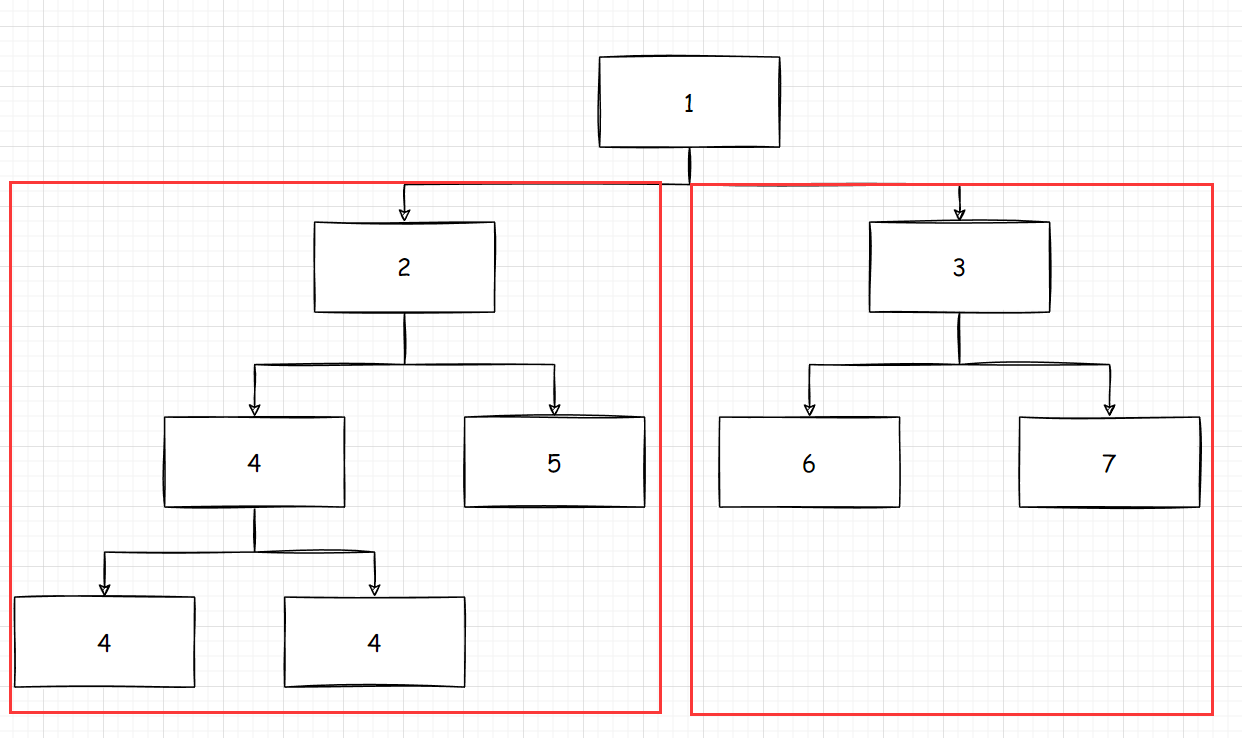
那么, 假设我们要统计左子树的节点数, 其实就变成了统计以2为根节点的树的节点个数
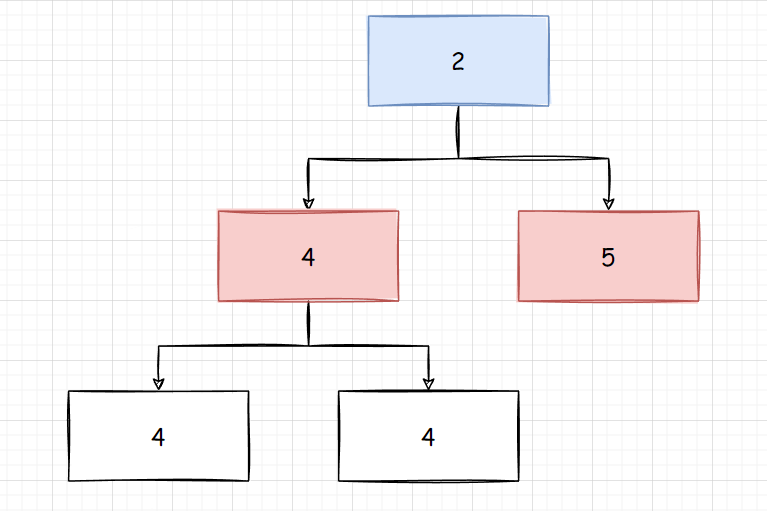
进一步分解, 假设我们要统计上面树的节点数, 就变成了统计左子树 4 和右子树 5 的两棵子树的节点数的子问题, 这个问题逐渐分解, 分解到最小单位

统计上面这样一棵树的节点个数, 这棵树同样是需要统计左子树的节点数 + 右子树的节点数 + 1(root)
思考 : 假设一个大的计算整棵树的大问题, 可以像现在这样一步一步的分解成一个个子问题的情况下, 我们就可以使用递归
递归流程
下面的流程是计算普通二叉树的流程 :
1.确定函数参数以及返回值
- 这个函数的目的是为了计算一棵树的总的节点数, 所以参数为
count(TreeNode root) - 返回值为 int , 也就是树的节点数
private int count(TreeNode root)
2.终止条件
我们在设置终止条件时, 一定要将问题分解到最小时, 去考虑终止条件, 一定不能在大问题上去考虑, 就比如这道题,

- 左右节点都为 NULL , 直接返回 1 , 因为只有root节点存在
3.当前层逻辑
当前层也就是左右节点至少有一个存在, 需要统计左右, 或者某一个
- 左节点存在, 右节点为NULL , 此时就要去统计 左子树的节点数 + 1 (root) :
1 + count(root.left) - 左节点为NULL, 右节点存在 (本题是二叉树, 不存在这样的情况, 但是我们暂时也把这种情况放进去, 适用于所有的树) :
1 + count(root.right) - 左节点都存在, 则需要统计左子树 和 右子树节点数
实际上本题是完全二叉树, 满二叉树的计算公式是假设层数是h, 节点数是 2 h − 1 2^h - 1 2h−1 , 只需要让指针分别从左右两边遍历计算深度, 判断是否一致,
如果是满二叉树, 直接使用公式计算, 如果不是, 按照普通二叉树计算即可
递归代码
1.代码实现
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int countNodes(TreeNode root) {
if(root == null) {
return 0;
}
return count(root);
}
private int count(TreeNode root) {
// 处理全空的情况
if(root.left == null && root.right == null) {
return 1;
}
// 处理只有一个节点为空
if(root.left == null && root.right != null) {
return 1 + count(root.right);
}
if(root.left != null && root.right == null) {
return 1 + count(root.left);
}
// 左右都不为空
int leftCount = count(root.left);
int rightCount = count(root.right);
// 左右子树的节点数量 + 本身的
return leftCount + rightCount + 1;
}
}
上面的代码是为了便于理解, 如果想要简化的话, 很简单 :
class Solution {
public int countNodes(TreeNode root) {
if (root == null) return 0;
return 1 + countNodes(root.left) + countNodes(root.right);
}
}
2.优化版
优化版是考虑了满二叉树, 先判断从左边遍历和从右边遍历的层高是否相同, 如果相同则可以使用 公式直接计算, 不同再使用普通方法计算
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int countNodes(TreeNode root) {
TreeNode le = root, ri = root;
// 判断是否是完全二叉树
int hl = 0, hr = 0;
while(le != null) {
le = le.left;
hl++;
}
while(ri != null) {
ri = ri.right;
hr++;
}
if(hl == hr) {
return (int)Math.pow(2, hl) -1;
}
return 1 + countNodes(root.left) + countNodes(root.right);
}
}
3.时间复杂度分析
计算普通树递归的时间复杂度是
O
(
n
)
O(n)
O(n) , 因为其实是访问了所有的节点, 计算满二叉树的时间复杂度是层高
O
(
l
o
g
N
)
O(log_{N})
O(logN) ,
N
N
N 是节点的个数,
h
h
h 是层高
N
=
2
h
−
1
=
=
>
h
=
l
o
g
N
+
1
N = 2^h - 1 ==> h = log_{N+1} \\
N=2h−1==>h=logN+1
但是实际上的时间复杂度是
O
(
l
o
g
N
∗
l
o
g
N
)
O(log_{N} * log_{N})
O(logN∗logN) , 因为最坏情况一定有一半是满二叉树. 另一半是完全二叉树
-
第一层, root
-
第二层, 有两棵树, 右边是满二叉树 : l o g N logN logN, 左边不确定
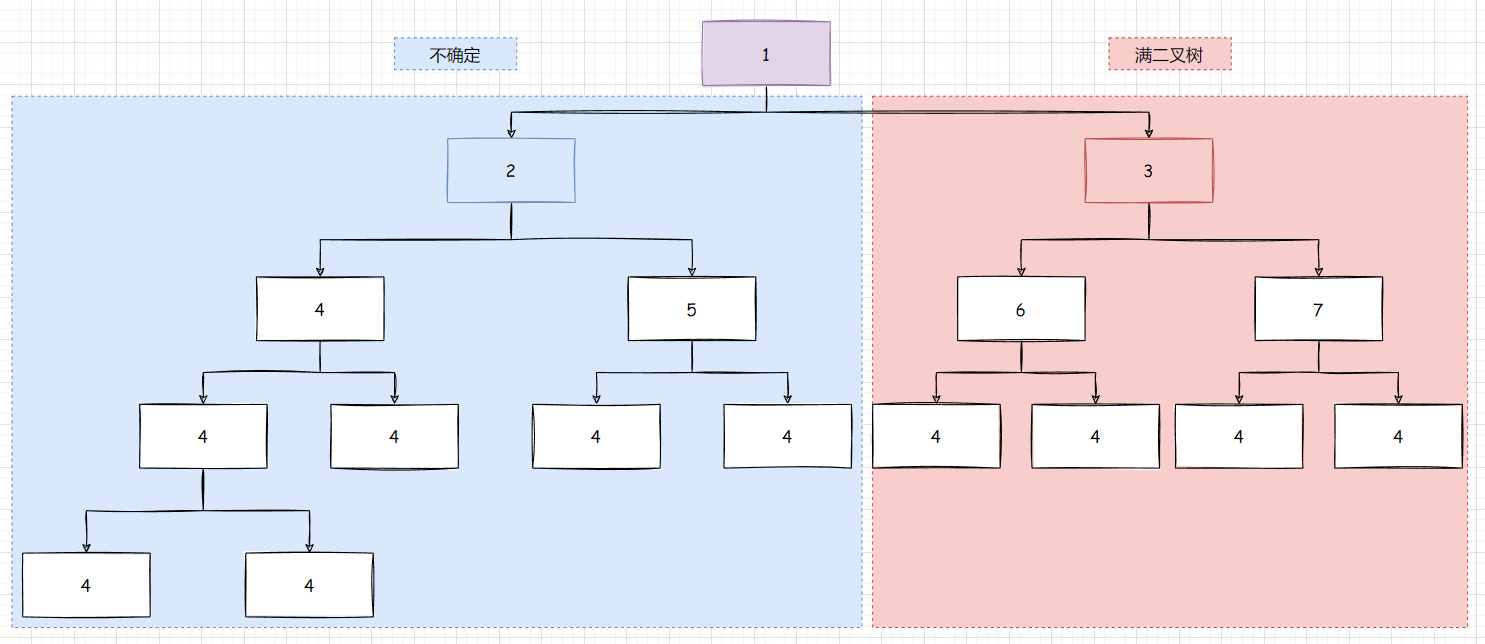
- 第三层, 右边满二叉树 : l o g N logN logN , 左边不确定
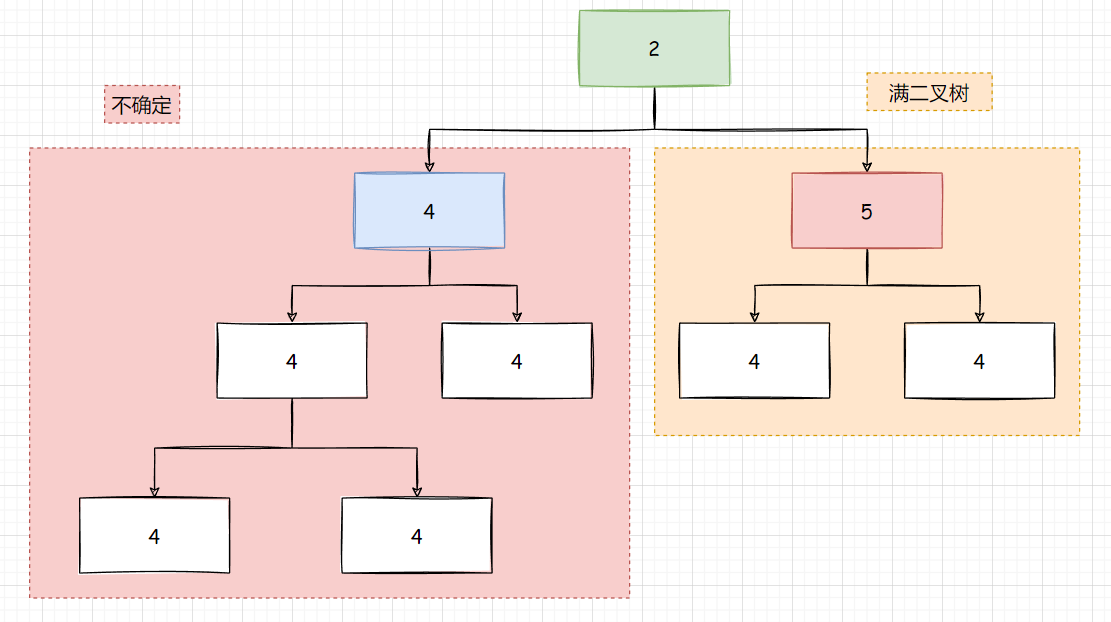
- 第四层, 右边满二叉树 : l o g N logN logN , 左边不确定
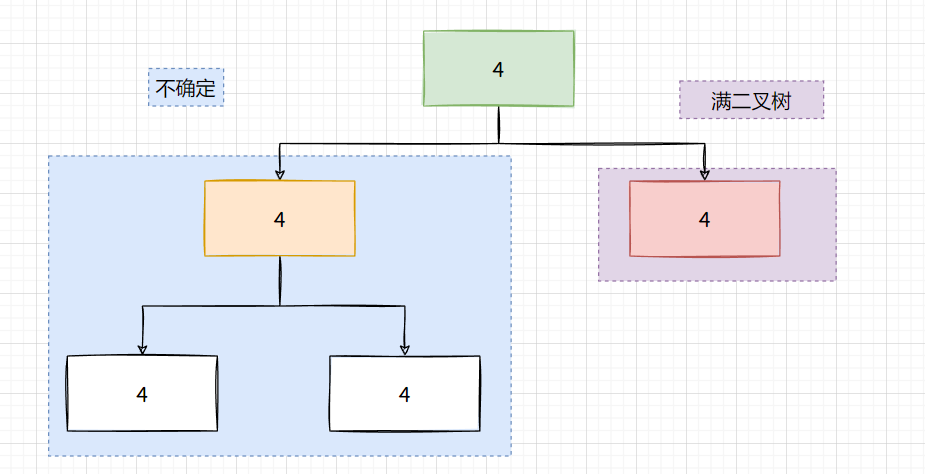
- 第五层, 也就是最后一层, 都是完全二叉树

层高是 O ( l o g N ) O(logN) O(logN) , 每一层需要计算的时间复杂度是 O ( l o g N ) O(logN) O(logN) , 所以实际上的时间复杂度是 O ( l o g N ∗ l o g N ) O(logN * logN) O(logN∗logN)