P1003 [NOIP2011 提高组] 铺地毯
题目描述
原题点这里-->P1003 [NOIP2011 提高组] 铺地毯 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
为了准备一个独特的颁奖典礼,组织者在会场的一片矩形区域(可看做是平面直角坐标系的第一象限)铺上一些矩形地毯。一共有 n 张地毯,编号从 11 到 n。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设,后铺的地毯覆盖在前面已经铺好的地毯之上。
地毯铺设完成后,组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意:在矩形地毯边界和四个顶点上的点也算被地毯覆盖。
输入格式
输入共 n+2 行。
第一行,一个整数 n,表示总共有 n 张地毯。
接下来的 n 行中,第 i+1 行表示编号 i 的地毯的信息,包含四个整数a,b,g,k,每两个整数之间用一个空格隔开,分别表示铺设地毯的左下角的坐标 (a,b) 以及地毯在 x 轴和 y 轴方向的长度。
第 n+2 行包含两个整数 x 和 y,表示所求的地面的点的坐标 (x,y)。
输出格式
输出共 1 行,一个整数,表示所求的地毯的编号;若此处没有被地毯覆盖则输出 -1。
输入输出样例
输入 #1
3 1 0 2 3 0 2 3 3 2 1 3 3 2 2
输出 #1
3
输入 #2
3 1 0 2 3 0 2 3 3 2 1 3 3 4 5
输出 #2
-1
说明/提示
【样例解释 1】
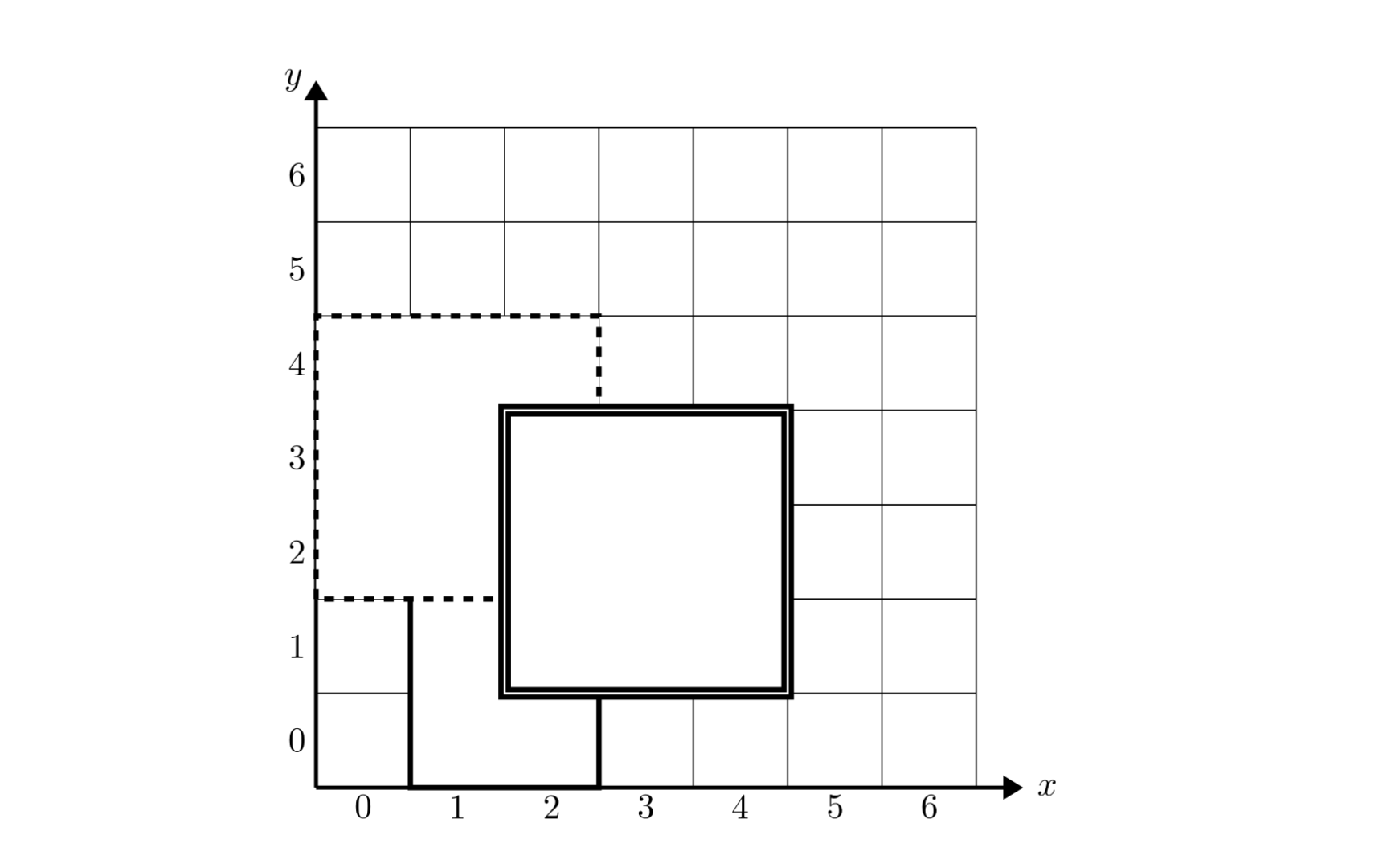
如下图,11 号地毯用实线表示,22 号地毯用虚线表示,33 号用双实线表示,覆盖点 (2,2)(2,2) 的最上面一张地毯是 33 号地毯。
【数据范围】
对于 30%30% 的数据,有 n≤2。
对于 50%50% 的数据,0≤a,b,g,k≤100。
对于 100%100% 的数据,有 0≤n≤10000, 0≤a,b,g,k≤100000。
解题过程
找到最后一块覆盖目标点的地毯即可,所以我们从后往前遍历每块地毯,寻找能覆盖目标点的地毯。如果地毯的左下角横纵坐标小于等于目标点的横纵坐标,并且地毯的右上角横纵坐标大于等于目标点的横纵坐标,说明该地毯覆盖目标点。
源代码
#include<stdio.h>
typedef struct{
int x,y,lx,ly;//地毯左下角坐标和地毯x,y轴上的长度
}DT;
DT dt[10010];//储存每块地毯的数据
int main()
{
int n,kx,ky;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d%d%d%d",&dt[i].x,&dt[i].y,&dt[i].lx,&dt[i].ly);
}
scanf("%d%d",&kx,&ky);
//从最后一块地毯往前遍历
for(int i=n;i>=1;i--)
{
//如果地毯的左下角横纵坐标小于等于目标点的横纵坐标,并且地毯的右上角横纵坐标大于等于目标点的横纵坐标,说明该地毯覆盖该点
if(dt[i].x<=kx&&dt[i].y<=ky&&dt[i].x+dt[i].lx>kx&&dt[i].y+dt[i].ly>ky)
{
printf("%d",i);
return 0;
}
}
//没有覆盖目标点的地毯输出-1
printf("-1");
return 0;
}
P1067 [NOIP2009 普及组] 多项式输出
题目描述
原题点这里-->P1067 [NOIP2009 普及组] 多项式输出 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
一元 n 次多项式可用如下的表达式表示:
f(x)=anxn+an−1xn−1+⋯+a1x+a0,an=0
其中,aixi 称为 i 次项,ai 称为 i 次项的系数。给出一个一元多项式各项的次数和系数,请按照如下规定的格式要求输出该多项式:
-
多项式中自变量为 x,从左到右按照次数递减顺序给出多项式。
-
多项式中只包含系数不为 0 的项。
-
如果多项式 n 次项系数为正,则多项式开头不出
+号,如果多项式 n 次项系数为负,则多项式以-号开头。 -
对于不是最高次的项,以
+号或者-号连接此项与前一项,分别表示此项系数为正或者系数为负。紧跟一个正整数,表示此项系数的绝对值(如果一个高于0 次的项,其系数的绝对值为 11,则无需输出 1)。如果 x 的指数大于 1,则接下来紧跟的指数部分的形式为“xb”,其中 b 为 x 的指数;如果 x 的指数为 1,则接下来紧跟的指数部分形式为 x;如果 x 的指数为 0,则仅需输出系数即可。 -
多项式中,多项式的开头、结尾不含多余的空格。
输入格式
输入共有 2 行
第一行 1 个整数,n,表示一元多项式的次数。
第二行有 n+1 个整数,其中第 i 个整数表示第 n−i+1 次项的系数,每两个整数之间用空格隔开。
输出格式
输出共 1 行,按题目所述格式输出多项式。
输入输出样例
输入 #1
5 100 -1 1 -3 0 10
输出 #1
100x^5-x^4+x^3-3x^2+10
输入 #2
3 -50 0 0 1
输出 #2
-50x^3+1
说明/提示
NOIP 2009 普及组 第一题
对于100%数据,0≤n≤100,−100≤系数≤100
解题过程
将输出内容拆成两部分(系数部分和指数部分)考虑即可。需要充分考虑各种情况。
源代码
#include<stdio.h>
int main()
{
int n;
scanf("%d",&n);
int a;
int t=n;
while(t>=0)
{
scanf("%d",&a);
//输出系数部分
if(n==0)
{
printf("%d",a);
}
else if(a==0)
{
}
else if(t==n)
{
if(a!=1&&a!=-1)
printf("%d",a);
if(a==-1)
printf("-");
}
else if(t!=0)
{
if(a!=1&&a!=-1)
printf("%+d",a);
if(a==-1)
printf("-");
if(a==1)
printf("+");
}
else
{
printf("%+d",a);
}
//输出次数部分
if(a&&t)
{
if(t==1)
printf("x");
else
printf("x^%d",t);
}
t--;
}
return 0;
}
P1540 [NOIP2010 提高组] 机器翻译
题目描述
原题点这里-->P1540 [NOIP2010 提高组] 机器翻译 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
小晨的电脑上安装了一个机器翻译软件,他经常用这个软件来翻译英语文章。
这个翻译软件的原理很简单,它只是从头到尾,依次将每个英文单词用对应的中文含义来替换。对于每个英文单词,软件会先在内存中查找这个单词的中文含义,如果内存中有,软件就会用它进行翻译;如果内存中没有,软件就会在外存中的词典内查找,查出单词的中文含义然后翻译,并将这个单词和译义放入内存,以备后续的查找和翻译。
假设内存中有 M 个单元,每单元能存放一个单词和译义。每当软件将一个新单词存入内存前,如果当前内存中已存入的单词数不超过 M−1,软件会将新单词存入一个未使用的内存单元;若内存中已存入 M 个单词,软件会清空最早进入内存的那个单词,腾出单元来,存放新单词。
假设一篇英语文章的长度为 N 个单词。给定这篇待译文章,翻译软件需要去外存查找多少次词典?假设在翻译开始前,内存中没有任何单词。
输入格式
共 2 行。每行中两个数之间用一个空格隔开。
第一行为两个正整数M,N,代表内存容量和文章的长度。
第二行为 N 个非负整数,按照文章的顺序,每个数(大小不超过 1000)代表一个英文单词。文章中两个单词是同一个单词,当且仅当它们对应的非负整数相同。
输出格式
一个整数,为软件需要查词典的次数。
输入输出样例
输入 #1
3 7 1 2 1 5 4 4 1
输出 #1
5
说明/提示
样例解释
整个查字典过程如下:每行表示一个单词的翻译,冒号前为本次翻译后的内存状况:
1:查找单词 1 并调入内存。1 2:查找单词 2 并调入内存。1 2:在内存中找到单词 1。1 2 5:查找单词 5 并调入内存。2 5 4:查找单词 4 并调入内存替代单词 1。2 5 4:在内存中找到单词 4。5 4 1:查找单词 1 并调入内存替代单词 2。
共计查了 55 次词典。
数据范围
- 对于 10%10% 的数据有 M=1,N≤5;
- 对于 100%100% 的数据有 11≤M≤100,1≤N≤1000。
解题过程
第n-1个需要存入内存的数存储在内存的第(n-1)%M个位置(从第0个位置开始存)。
源代码
#include<stdio.h>
bool a[1005];//a[i]用于判断i是否在内存中
int nc[105];//记录内存中储存的数
int b=0;
int main()
{
int m,n;
scanf("%d%d",&m,&n);
//初始化nc数组中的数为-1
for(int i=0;i<=m;i++)
nc[i]=-1;
int t;
for(int i=0;i<n;i++)
{
scanf("%d",&t);
if(!a[t])//内存中没有
{
a[nc[b%m]]=false;
a[t]=true;
nc[b%m]=t;//将t存入内存,将内存中的第b%m位移出内存
b++;//每次内存中找不到都需要往内存中存储一次
}
}
printf("%d",b);
return 0;
}