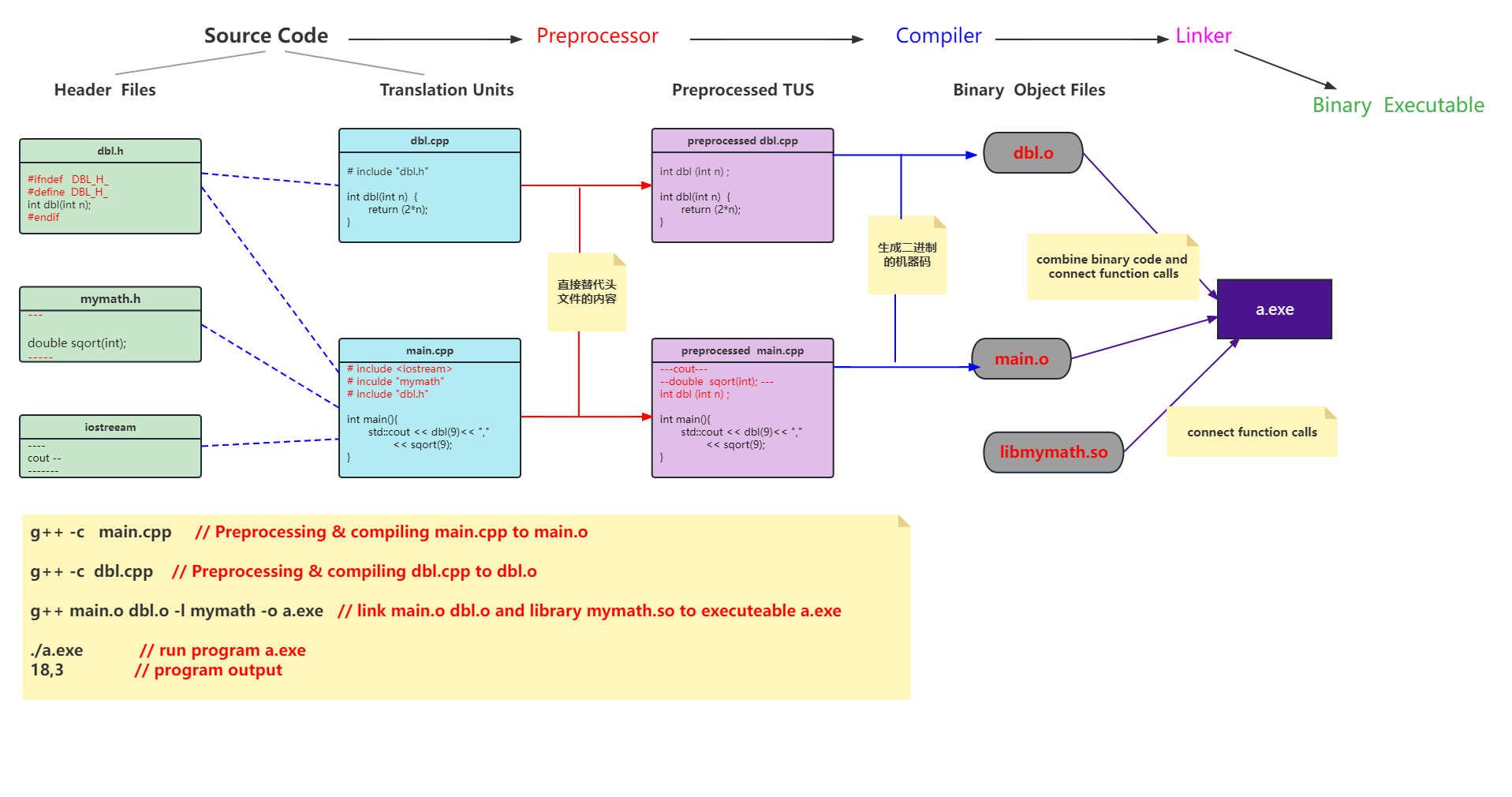
503.下一个更大元素2

和下一个更大元素基本相同，就多了一个循环数组的问题
处理方法：
循环的次数*2
利用i%nums.size()得到处理的下标，这样当遍历到nums的最后一个元素的时候，向单调栈中插入其下标nums.size()-1,之后将其与下标nums.size()%nums.size()，即下标为0的元素进行值的比较，达到循环数组的目的。
而之后知道结束for循环的操作，就与之前第一遍的时候重复了
这样也不需要改变result数组的大小，在结束for循环之后直接将result数组返回即可

42.接雨水

双指针法（超时）

遍历每一列（除第一列和最后一列），找到左侧最高的高度lHeight和右侧最高的高度rHeight。取二者的最小高度值，其和第i列的高度差，如果大于0，就是第i列可以接的雨水量
将每一列的接雨水量累加求得
时间复杂度O(n^2), 空间复杂度O(1)

动态规划

本质和双指针法相同，只不过用了动态规划的方法来得到左边和右边的最大高度，减少了时间复杂度

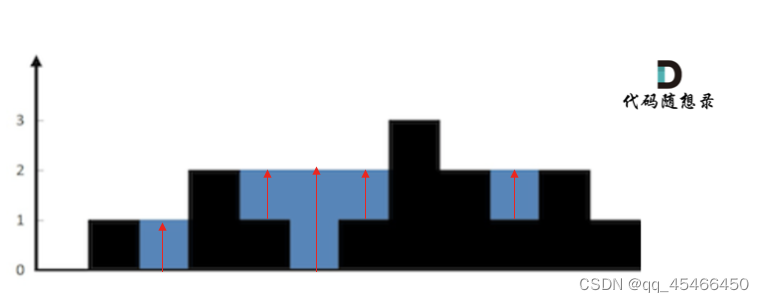
单调栈

按照行计算

栈内保存柱子的下标
开始将下标0push到st中，循环遍历柱子，如果柱子对应的高度值<=height[st.top()]，则将下标push到栈中。如果柱子对应的高度值>height[st.top()],height[i]就是底部右侧的高度。先记录底部的高度mid=height[st.top()],之后pop()。这时栈顶的元素就是底部左侧的高度。
取左侧和右侧的较小高度-底部高度mid，则得到了凹槽底部高度h。
右侧下标-左侧下标-1得到凹槽底部宽度w int w = i - st.top() - 1;
sum += h * w;得到雨滴总数