0. 引言
我们考虑如何计算一个图连通分量的个数. 假定简单无向图
G
G
G有两个连通分量(子图)
G
1
,
G
2
G_1, G_2
G1,G2, 如下图所示:
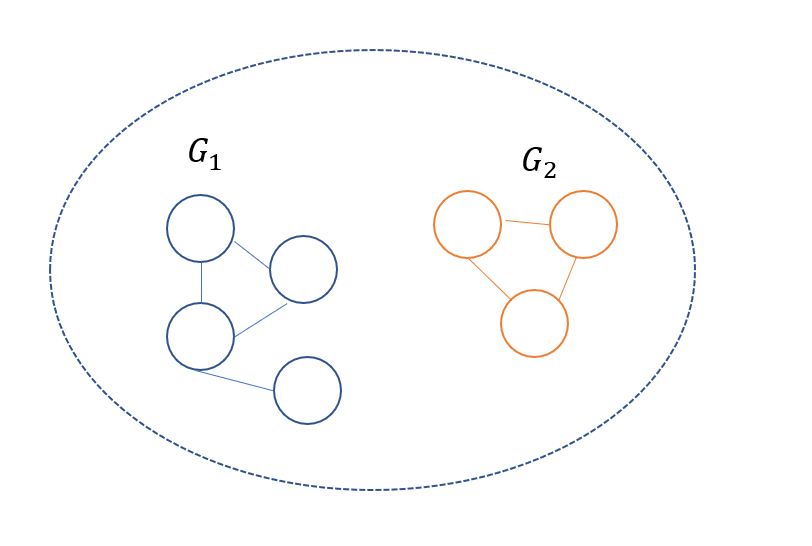
一个很自然的想法是, 要想求连通分量个数, 我们可以使用Full-DFS算法, 也就是我们从某个点开始深度优先搜索, 并标记访问过的元素. 随后挨个顶点判断, 如果某个点没有被访问过, 则接着从该点进行深度优先搜索, 这样深度优先搜索的次数就是连通量的个数.
除此之外, 我们还可以用并查集来求图中连通分量的个数. 并查集, 顾名思义, 有并与查两部分. 并, 就是合并(join, union), 即利用某种规则将两个顶点合并为一个连通分量. 查, 就是查询(find), 用以查询某个节点所属连通分量的代表性节点.
例如, 某个单位里, 有两个帮派. 一个员工A和另一个员工B相遇了, 两个人想知道自己是不是同属一个帮派. 于是, 两个人可以互相报上自己帮派的老大, 是局长还是书记. 如果两个人的老大一样, 则两个人就是同属一个帮派, 否则不是.
抽象出来, 我们将每个连通分量都选出一个代表的节点, 这个节点就是老大, 该连通分量中其他的节点或直接, 或间接地与老大相连. 一个单位帮派的个数可以用老大的个数来代表.
下面说具体如何去并, 查
1. 查, find
一个连通图总可以表示成一个生成树(例如, 单位里的一个帮派总可以捋出来一个上下级关系), 例如,
G
1
G_1
G1子图中, 假设每个节点有编号, 那么假定有如图的一种连接关系(生成树):
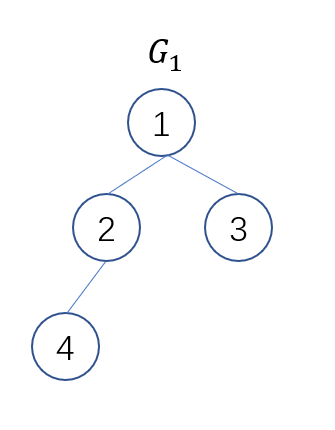
1是老大, 下面是2, 3, 4是老末. 如果我们用一个数组
p
a
r
e
n
t
[
N
]
parent[N]
parent[N]表示这种上下级关系, 也就是
p
a
r
e
n
t
[
i
]
=
j
parent[i]=j
parent[i]=j表示i的上级为j, 则上图的关系可以表示为:
parent[4] = 2
parent[2] = 1
parent[3] = 1
parent[1] = 1
所以, 只有老大的上级才是他自己. 如果给我们一个4, 想查一下, 4的老大是谁? 我们就可以这样一层一层查上去:
parent[4] = 2
parent[2] = 1
parent[1] = 1, Done!!!
当找到满足parent[i] = i的i, 就表示找到了老大(子图的代表)为i.
我们可以用代码这样表示:
int find(int x) {
while (parent[x] != x) x = parent[x]; // 只要没找到, 就沿着上级继续找
return x; // 找到了, 返回
}
但是, 假如一个倒霉催的结构是这样的:
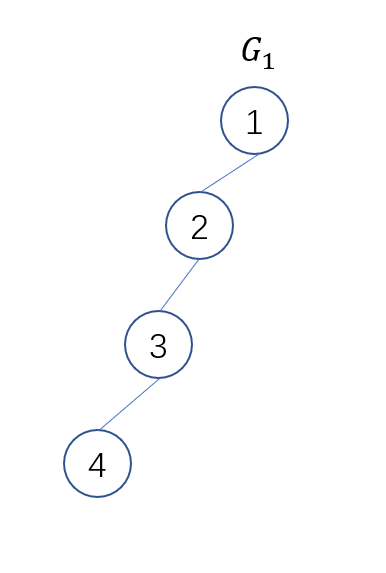
那我们就需要花费
O
(
n
)
O(n)
O(n)的时间去找, 这是因为不平衡的树会带来更大的时间复杂度(最坏的情况为
O
(
n
)
O(n)
O(n)). 为此, 既然我们只是找老大, 我们直接让每个人直接对老大负责不好么?
我们如何做到这一点? 我们用递归来实现. 对于不满足parent[i] = i的i, 我们直接让i的上级parent[i]等于老大, 也就是parent[i] = find(parent[i]), 这样递归下去就可以达到上图的结果. 需要说明的是, 这样整理好之后, 以后的查询才会省时间. 换言之, 第一次是不会节约时间的. 于是现在的find函数可以写为:
int find(int i) {
if (parent[i] != i) // 没有找到
parent[i] = find(parent[i]); // 让i的上级是老大
return parent[i]; // 返回老大
}
2. 并, union, join
如果说, 单位里的两个派别准备重修旧好, 也就是两个派别要合并. 然而, 一个派别只能有一个老大, 所以两个派别的老大就必须有一个要屈尊, 不再当老大, 成为另一个老大的下属, 这样的话, 不论两个派别的哪个人, 最终都可以查询到新的老大, 这就是并的过程, 用下图表示:
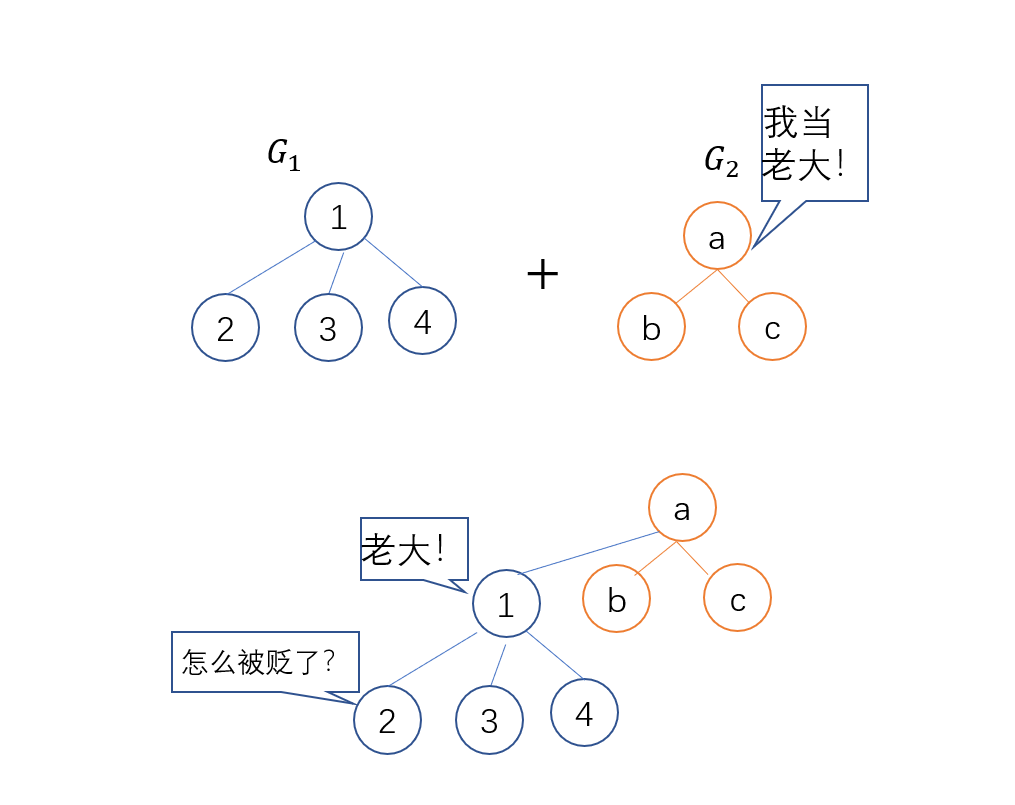
代码这么来描述:
void unoin(int x, int y){ // 合并俩派别, x, y为其中的成员
int px = find(x), py = find(y); // 找到他们各自的老大
if (px != py) parent[px] = py; // 让px的老大的老大为py
}
那么假如我们想指定一种合并的规则, 应该如何做呢? 假设我们标记节点的深度, 如图所示:
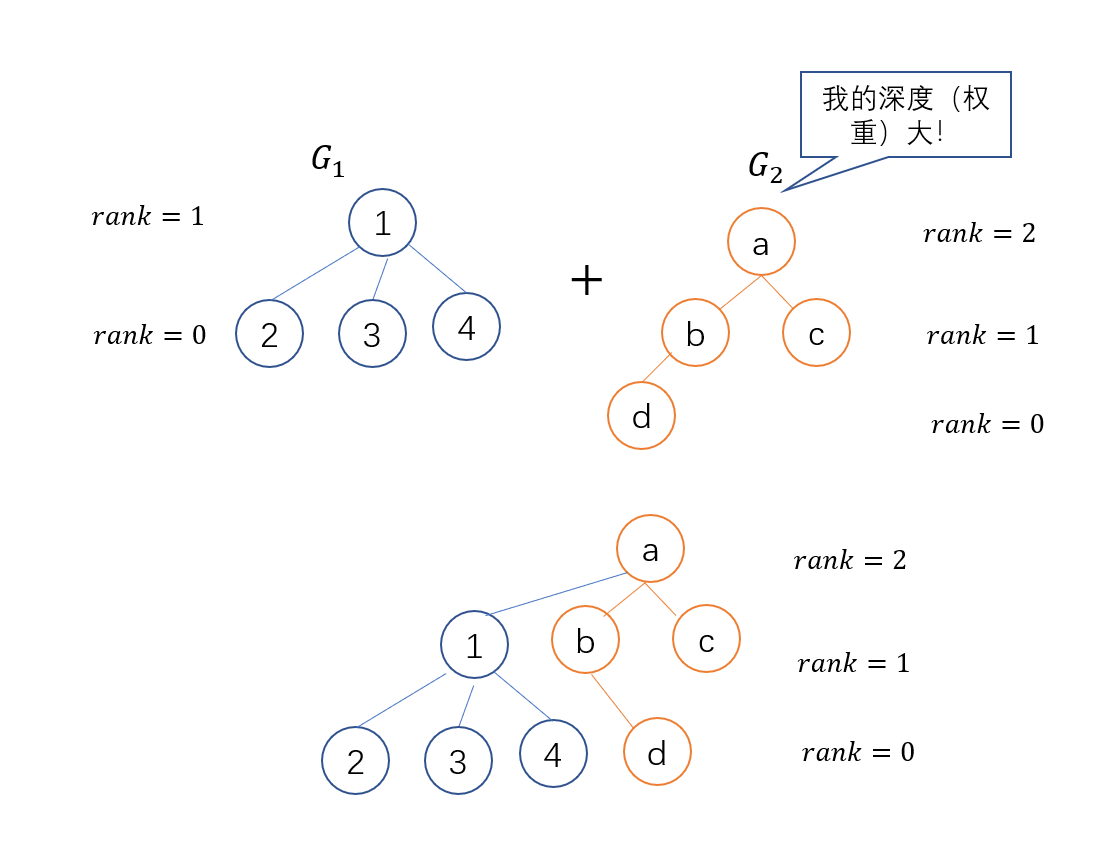
因此, 为了不让树产生退化(合并后左右子树的高度差尽可能小), 我们将深度小的合并到深度大的. 如果二者的深度相同, 则可以随便指定一个作为新老大, 随后将新老大的权值加1, 如图:
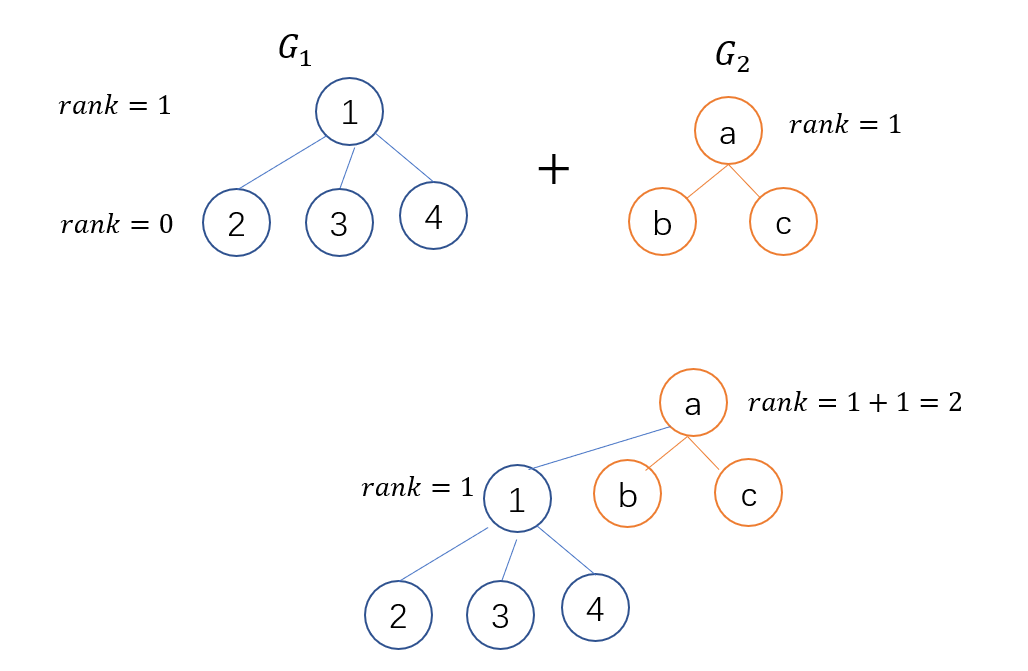
代码如下:
void unoin(int x, int y) {
// 寻找x, y的老大
int px = find(x), py = find(y);
if (px != py) {
// 如果x的权重大 让y的老大为x
if (rank[px] > rank[py]) parent[py] = px;
else { // 否则 让x的老大为y
if (rank[px] == rank[py]) rank[py]++; // 如果权重相等 则先将y的权重加1
parent[px] = py;
}
}
}
3. 例题
下面用几道例题说明并查集的使用. 难度从低到高.
3.1 最长连续序列
题目链接: LeetCode128
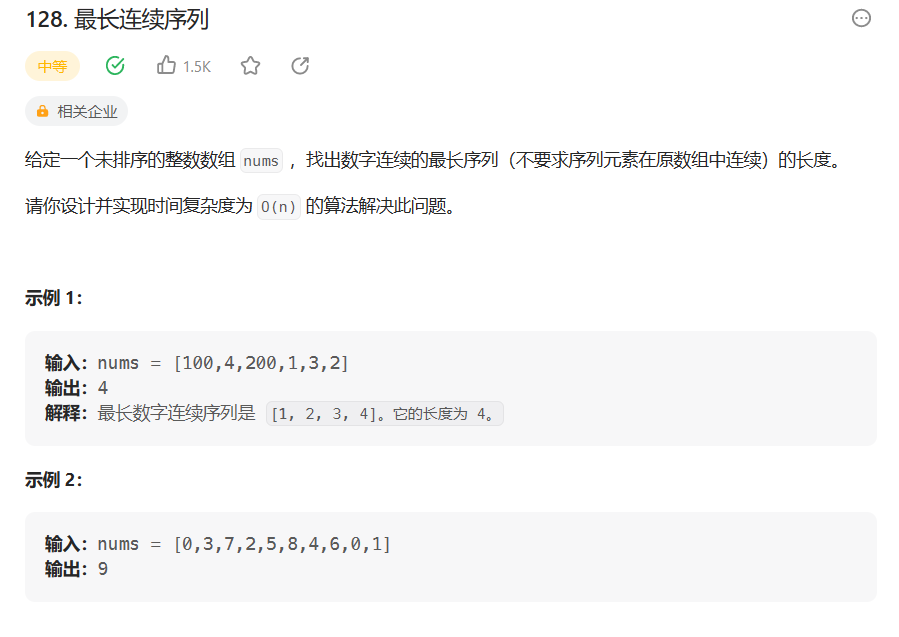
这个题让我们在数组中找到一个最长的连续数字序列. 如果我们将元素视为图里的节点, 每一段连续的数字序列作为一个子图, 就是要找到节点最多的子图.
为此, 我们对于数组元素num, 假如num + 1也在数组中, 则将num所在的子图与num + 1所在的子图并在一起. 除此之外, 我们还需要用一个额外的哈希表记录每个子图的大小, 键为子图的老大, 值为子图的大小.
代码:
class Solution {
public:
unordered_map<int, int> pre, regionResult; // pre: 储存父节点 regionResult: 节点所在连通域面积
int find(int x) { // 查
if (x == pre[x]) return x;
else {
pre[x] = find(pre[x]);
return pre[x];
}
}
int merge(int x, int y) { // 并
x = find(x), y = find(y);
if (x == y) return regionResult[x];
// 若不相等 并到一起
pre[y] = x;
regionResult[x] += regionResult[y]; // 把大小加一起并返回
return regionResult[x];
}
int longestConsecutive(vector<int>& nums) {
if (!nums.size()) return 0;
int result = 1;
// 初始化
for (int num : nums) {
pre[num] = num;
regionResult[num] = 1;
}
// 合并相邻数 并更新结果 注意只合并num与num+1 不需要合并num与num-1 否则重复
for (int num : nums) {
if (pre.count(num + 1))
result = max(result, merge(num, num + 1));
}
return result;
}
};
3.2. 危险程度
题目链接: Acwing4796

这个题是说, 有一个试管, 初始时危险值为1. 现在往里面导入物质, 假如要倒入的物质可以和试管里面任一一种物质反应, 则将危险值乘2. 问可以达到的最大危险值为多少.
我们可以构建图来解决这个问题. 假如a与b反应, b与c反应, 则a, b, c可以构成一个连通子图. 于是n个物质就构成了若干个连通子图, 每个子图中的物质可以与子图中其他若干个物质发生反应. 所以, 对于一个有t个节点的子图, 可以达到最大的危险值为
2
t
−
1
2^{t-1}
2t−1, 证明如下:
例如假设四种物质a,b,c,d的反应关系如下(如果不是严格的树(即有环), 也一定可以等价成如下的形式):
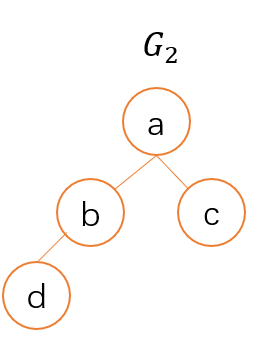
那么只要按照广度优先搜索的顺序倒入a->b->c->d, 就可以达到2^3=8的危险度. 且不同子图间是孤立的, 因此假设一共有k个子图, 每个子图的节点个数分别为
a
0
,
.
.
.
,
a
k
−
1
a_0, ..., a_{k-1}
a0,...,ak−1, 则最大的危险程度为
2
a
0
−
1
⋅
2
a
1
−
1
⋅
⋅
⋅
⋅
2
a
k
−
1
−
1
=
2
n
−
k
2^{a_0-1}·2^{a_1-1}····2^{a_{k-1}-1}=2^{n-k}
2a0−1⋅2a1−1⋅⋅⋅⋅2ak−1−1=2n−k
为此, 我们只需要求出连通子图的个数即可.
代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int parent[N]; // parent数组
int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
int main()
{
int n, m;
cin >> n >> m;
// 初始化并查集 每个指向自己
for (int i = 0; i < n; i ++ )
parent[i] = i;
int result = n; // 初始n个子图
while (m -- ) {
int x, y;
cin >> x >> y; // 能反应的两种物质
// 找到老大
x = find(x); y = find(y);
if (x != y) { // 合并两个子图
parent[x] = y;
result --;
}
}
cout << (1LL << (n - result)) << "\n";
return 0;
}
3.3. 岛屿数量
题目链接: LeetCode200
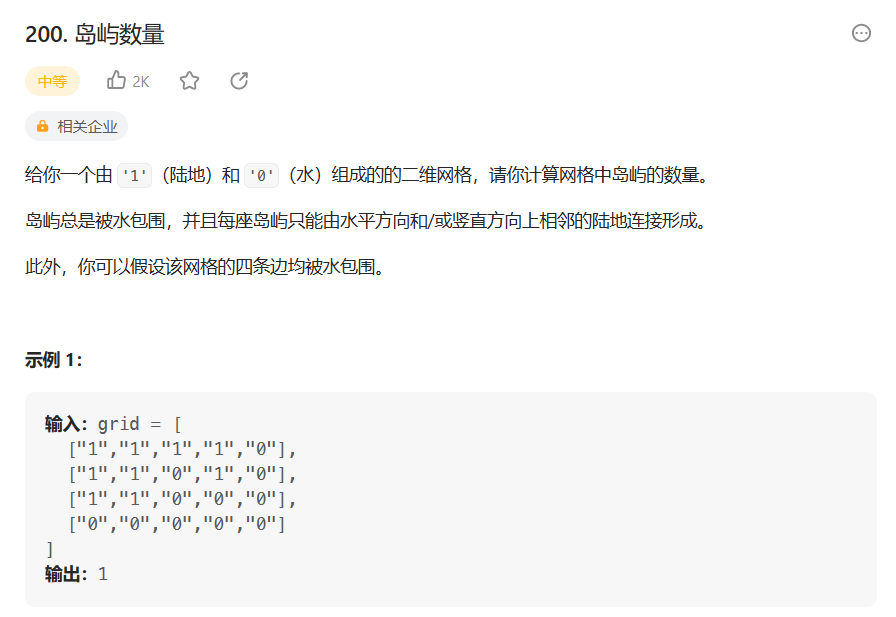
这个题的一种做法是, 跟玩扫雷一样, 但凡是扫到一个1, 那么执行深度优先搜索, 将与其相连的1都扫成0. 这样再碰到下一个1时, 一定是另一个岛屿, 所以岛屿的数量就是执行深度优先搜索的次数. 代码:
class Solution {
private:
int rows = 0, cols = 0;
public:
void dfs(vector<vector<char>>& grid, int row, int col) {
grid[row][col] = '0'; // 标记为0
// 上下左右, 深度优先
if (row > 0 && grid[row - 1][col] == '1') dfs(grid, row - 1, col);
if (col > 0 && grid[row][col - 1] == '1') dfs(grid, row, col - 1);
if (row < rows - 1 && grid[row + 1][col] == '1') dfs(grid, row + 1, col);
if (col < cols - 1 && grid[row][col + 1] == '1') dfs(grid, row, col + 1);
}
int numIslands(vector<vector<char>>& grid) {
this->rows = grid.size();
this->cols = grid[0].size();
int result = 0;
for (int row = 0; row < rows; row ++) {
for (int col = 0; col < cols; col ++) {
if (grid[row][col] == '1') {
dfs(grid, row, col);
result ++;
}
}
}
return result;
}
};
也可以用并查集来做. 每个'1', 我们都将其与周围的'1'连通, 则岛屿的数量就是连通图的数量.
class UnionFind {
public:
UnionFind(vector<vector<char>>& grid) {
count = 0;
int m = grid.size();
int n = grid[0].size();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == '1') {
parent.push_back(i * n + j);
++count;
}
else {
parent.push_back(-1);
}
rank.push_back(0);
}
}
}
int find(int i) {
if (parent[i] != i) {
parent[i] = find(parent[i]);
}
return parent[i];
}
void unite(int x, int y) {
int rootx = find(x);
int rooty = find(y);
if (rootx != rooty) {
if (rank[rootx] > rank[rooty])
parent[rooty] = rootx;
else {
if (rank[rootx] == rank[rooty]) rank[rooty] ++;
parent[rootx] = rooty;
}
count --;
}
}
int getCount() const {
return count;
}
private:
vector<int> parent;
vector<int> rank;
int count;
};
class Solution {
public:
int numIslands(vector<vector<char>>& grid) {
int nr = grid.size();
if (!nr) return 0;
int nc = grid[0].size();
UnionFind uf(grid);
int num_islands = 0;
for (int r = 0; r < nr; ++r) {
for (int c = 0; c < nc; ++c) {
if (grid[r][c] == '1') {
grid[r][c] = '0';
if (r - 1 >= 0 && grid[r-1][c] == '1') uf.unite(r * nc + c, (r-1) * nc + c);
if (r + 1 < nr && grid[r+1][c] == '1') uf.unite(r * nc + c, (r+1) * nc + c);
if (c - 1 >= 0 && grid[r][c-1] == '1') uf.unite(r * nc + c, r * nc + c - 1);
if (c + 1 < nc && grid[r][c+1] == '1') uf.unite(r * nc + c, r * nc + c + 1);
}
}
}
return uf.getCount();
}
};



![在Win10下装VMware17后,[ 安装VMware Tools ]选项灰色的解决办法](https://img-blog.csdnimg.cn/f0840d228e56441c9bb15bf668e19b29.png)