基于HMM隐马尔可夫模型的金融数据预测算法matlab仿真

news2024/10/6 22:38:25

1.程序功能描述

2.测试软件版本以及运行结果展示

3.核心程序

4.本算法原理

5.完整程序

1.程序功能描述

基于HMM隐马尔可夫模型的金融数据预测算法.程序实现HMM模型的训练，使用训练后的模型进行预测。

2.测试软件版本以及运行结果展示

MATLAB2022A版本运行

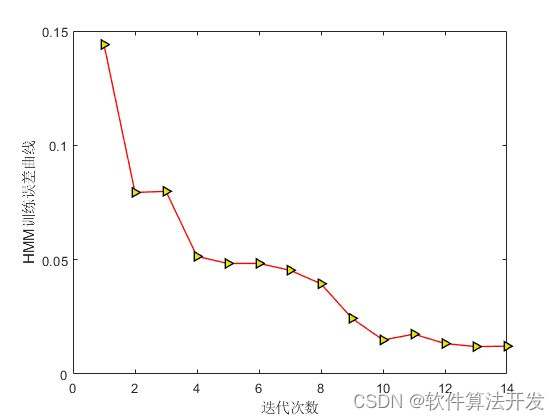
3.核心程序

......................................................................
% 初始化预测值矩阵yuce和误差矩阵err
yuce = zeros(size(data, 1), lens);
err = zeros(size(data, 1), lens);

% 计算并存储预测值及误差
for i = 1:size(data, 1)
    yuce(i, 1) = Prices(i, 1); % 第一天的预测值等于实际值
    for j = 2:lens
        tmps = 0; % 初始化临时变量
        for k = 1:Nstate
            % 计算状态转移和观测概率的乘积
            tmps = tmps + u(k) * tms(:, k); % u和tms是HMM模型参数
        end
        % 计算预测值
        yuce(i, j) = sum(post(j-1, :, i) .* tmps');
        % 计算预测误差
        err(i, j) = yuce(i, j) - Prices(i, j);
    end
end

% 绘制第一组数据的真实值和预测值曲线
figure;
plot(yuce(1,:), '.'); % 预测值曲线
hold on;
plot(Prices(1,:), 'r'); % 真实值曲线
grid on;
legend('预测值', '真实值');

% 绘制第一组数据的预测误差曲线
figure;
plot(yuce(1,:) - Prices(1,:), 'b-x'); % 预测误差曲线
grid on;
legend('预测误差');
ylim([-400, 400]); % 设置纵坐标的显示范围
41

4.本算法原理

隐马尔可夫模型（Hidden Markov Model, HMM）是一种概率模型，广泛应用于序列数据的建模与预测，尤其适用于金融市场时间序列分析，如股票价格走势预测、汇率波动分析等。HMM假设有一个不可观测的状态序列，每个状态生成一个可观测的符号，状态间的转移遵循一定的概率规律，而每个状态下生成的符号也服从某种概率分布。

基本概念与模型定义