93.复原IP地址

有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

• 例如："0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。

给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。

解题思路：

继续使用回溯递归

输入参数：def backtracking(s, start_index, path, result)

停止条件：if start_index == len(s) and len(path) == 4

回溯逻辑：检查是否valid，如果是的话进行回溯与递归

if is_valid(s, start_index, i):
                    path.append(s[start_index:i+1])
                    backtracking(s,i+1,path,result)
                    path.pop()

 代码如下：

class Solution:
    def restoreIpAddresses(self, s: str) -> List[str]:
        result = []
        #决定在哪里切割hwere to split:using start_index
        def backtracking(s, start_index, path, result):
            #stopping criterian
            if start_index == len(s) and len(path) == 4:
                result.append('.'.join(path))
                return
            if len(path) > 4:  # 剪枝
                return
            for i in range(start_index, len(s)):
                if is_valid(s, start_index, i):
                    path.append(s[start_index:i+1])
                    backtracking(s,i+1,path,result)
                    path.pop()
                
        def is_valid(s, start, end):            
            if start>end:
                # print('test')
                return False            
            if  s[start] == '0' and start != end:
                # print('test3')
                return False
            num = int(s[start:end+1])
            return 0 <= num <= 255
        backtracking(s, 0, [], result)
        return result

78.子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的

子集

（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

输入参数：def backtracking(nums, path, result, start)

停止条件：if start>=len(nums): return

回溯逻辑：设立start_index，每层从当前数字的下一个开始递归

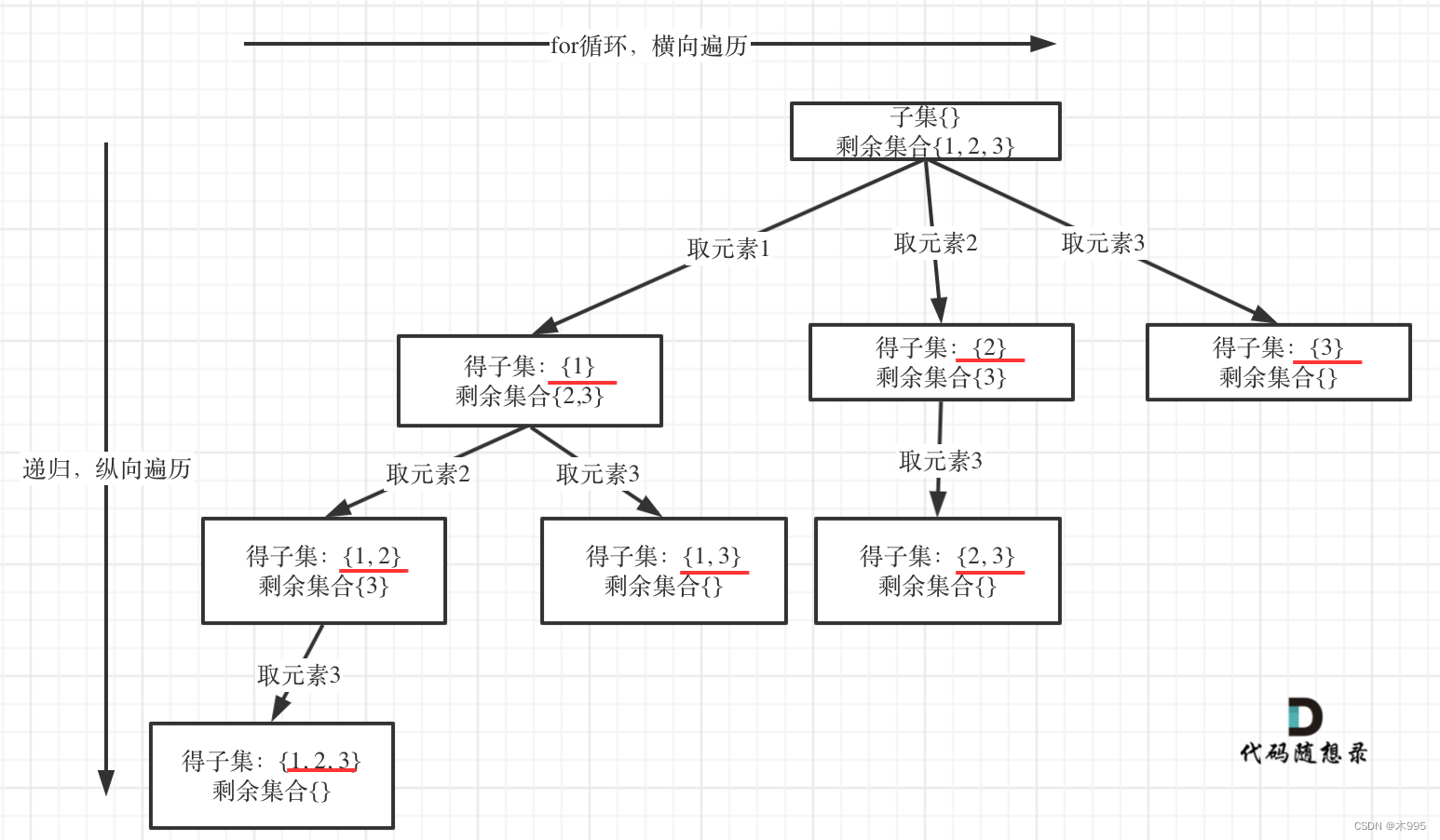
如图所示，本题与之前回溯问题不同在于在result中加入新集合并非在叶子节点，而是在每层递归时就加入，这样才能确保加入每个集合

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        path = []
        result = []
        def backtracking(nums, start_index):
            result.append(path[:])
            if start_index>=len(nums):
                return
            for i in range(start_index, len(nums)):
                path.append(nums[i])
                backtracking(nums, i+1)
                path.pop()
        backtracking(nums, 0)
        return result

90.子集II

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的 

子集

（幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

class Solution:
    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        path = []
        result = []
        nums = sorted(nums)
        used = [False]*len(nums)
        def backtracking(nums, start_index, used):
            result.append(path[:])
            if start_index >= len(nums):
                return
            for i in range(start_index, len(nums)):
                if i>0 and nums[i] == nums[i-1] and not used[i-1]:
                    continue
                print(nums[i])
                path.append(nums[i])
                used[i] = True
                backtracking(nums, i+1, used)
                used[i] = False
                path.pop()
        backtracking(nums, 0, used)
        return result