第一题
509. 斐波那契数
题目描述:斐波那契数(通常用 F(n) 表示)形成的序列称为斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例1:
输入:n = 4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3
思路
当我们写完回溯法的题目之后,看到这道题,第一个想法就是递归计算。
递归法
int fib(int n){
return dfs(n);
}
int dfs(int n){
if(n == 0){
return 0;
}
if(n == 1){
return 1;
}
return dfs(n - 1) + dfs(n - 2);
}
如果我们把递归树画出来,可以看到有重叠子问题。

这是动态规划和普通穷举法的不同,也是动态规划的第一个要素。普通穷举法,子问题之间互不重叠,所以画出来递归树也没有相同的节点;动态规划,子问题之间有重叠,所以画出来的递归树有相同节点。既然递归树有相同节点,那我们就可以通过剪枝来优化算法。我们可以用一个数组来记录节点,如果某个节点已经被记录在数组中,那就直接返回数组中的值,而不用进行递归求解。
递归法+dp数组
int fib(int n){
int[] dp = new int[n + 1];
return dfs(n, dp);
}
int dfs(int n, int[] dp){
if(n == 0){
return 0;
}
if(n == 1){
return 1;
}
if(dp[n] != 0){
return dp[n];
}
dp[n] = dfs(n - 1, dp) + dfs(n - 2, dp);
return dp[n];
}
这个时候我们再把递归树画出来,可以看到我们将递归树剪枝成了递归链表。
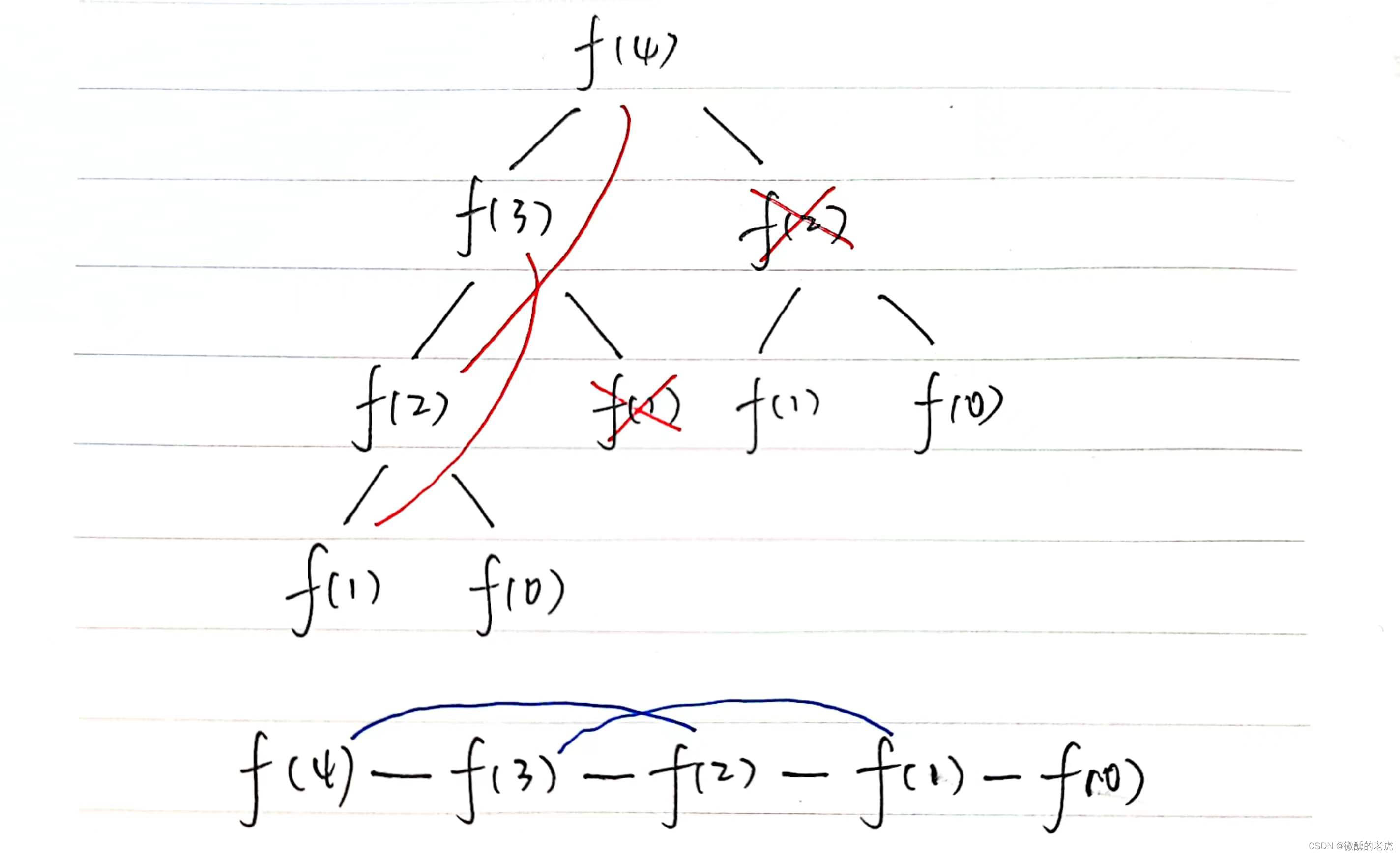
不难看出,现在问题转换成如何填充dp数组,我们可以对此继续进行优化。
迭代法(动态规划)
为了节省空间,我们可以放弃递归函数,用迭代循环的方式填充dp数组。
int fib(int n){
if(n < 2){
return n;
}
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;
for(int i = 2; i <= n; i++){
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
总结
动态规划与穷举法的联系与区别:
动态规划有重叠子问题。
动态规划三要素:
-
原问题可以拆解成重叠子问题
-
原问题的最优解由子问题的最优解构成
-
子问题到原问题有递推公式(状态转移方程)
第一条已经说明过了,后两条之后再说明。
动态规划解题步骤:
-
画出搜索树
-
确定搜索树节点的含义
-
确定搜索树节点连线的含义
-
确定dp数组的含义
-
列出递推公式
-
验证递推公式
后面详细说明这些解题步骤。
第二题
70. 爬楼梯
题目描述:假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例1:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
思路
借这道题,我们来好好讲讲动态规划解题步骤。
第一步,画出搜索树。
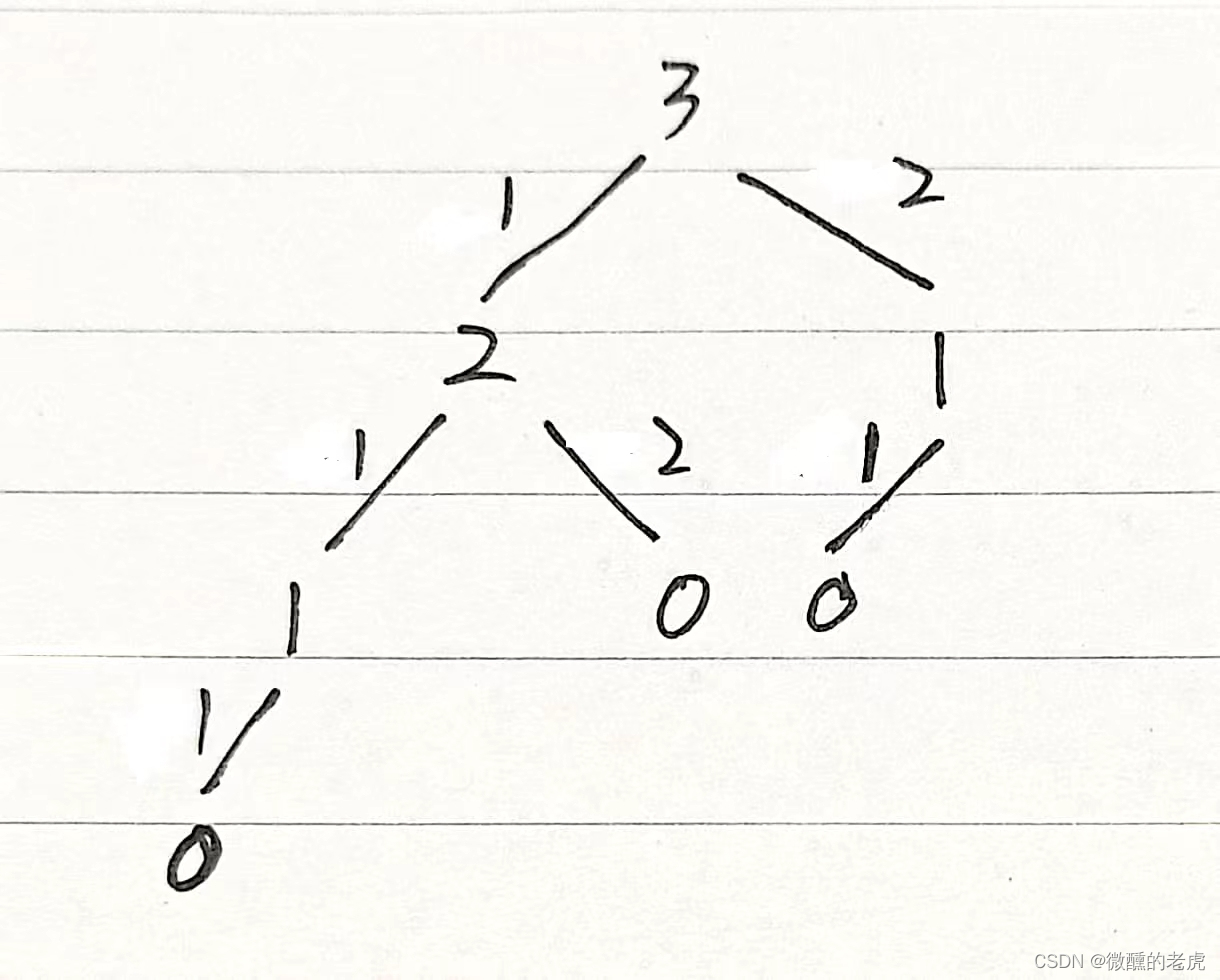
我们设定从0阶开始登楼梯,需要n阶才能到达楼顶,也就是需要从0阶开始爬到n阶。
看搜索树,到达第3阶有两种方法。第一种方法,先到达第2阶,然后再向上爬1阶。第二种方法,先到达第1阶,再向上爬2阶。
到达第2阶,也有两种方法。第一种方法,先到达第1阶,然后再向上爬1阶。第二种方法,先到达第0阶,再向上爬2阶。
到达第1阶,只有一种方法,先到达第0阶,再向上爬1阶。
第0阶,也就是出发的台阶,每次都从第0阶出发。
第二步,确定搜索树节点的含义。
刚刚的搜索树只是登楼梯的示意图,每个节点表示的是“所在的台阶”,3表示第3阶,2表示第2阶。现在,要把“到达该台阶的方法”也添加到节点上,搜索树如下。
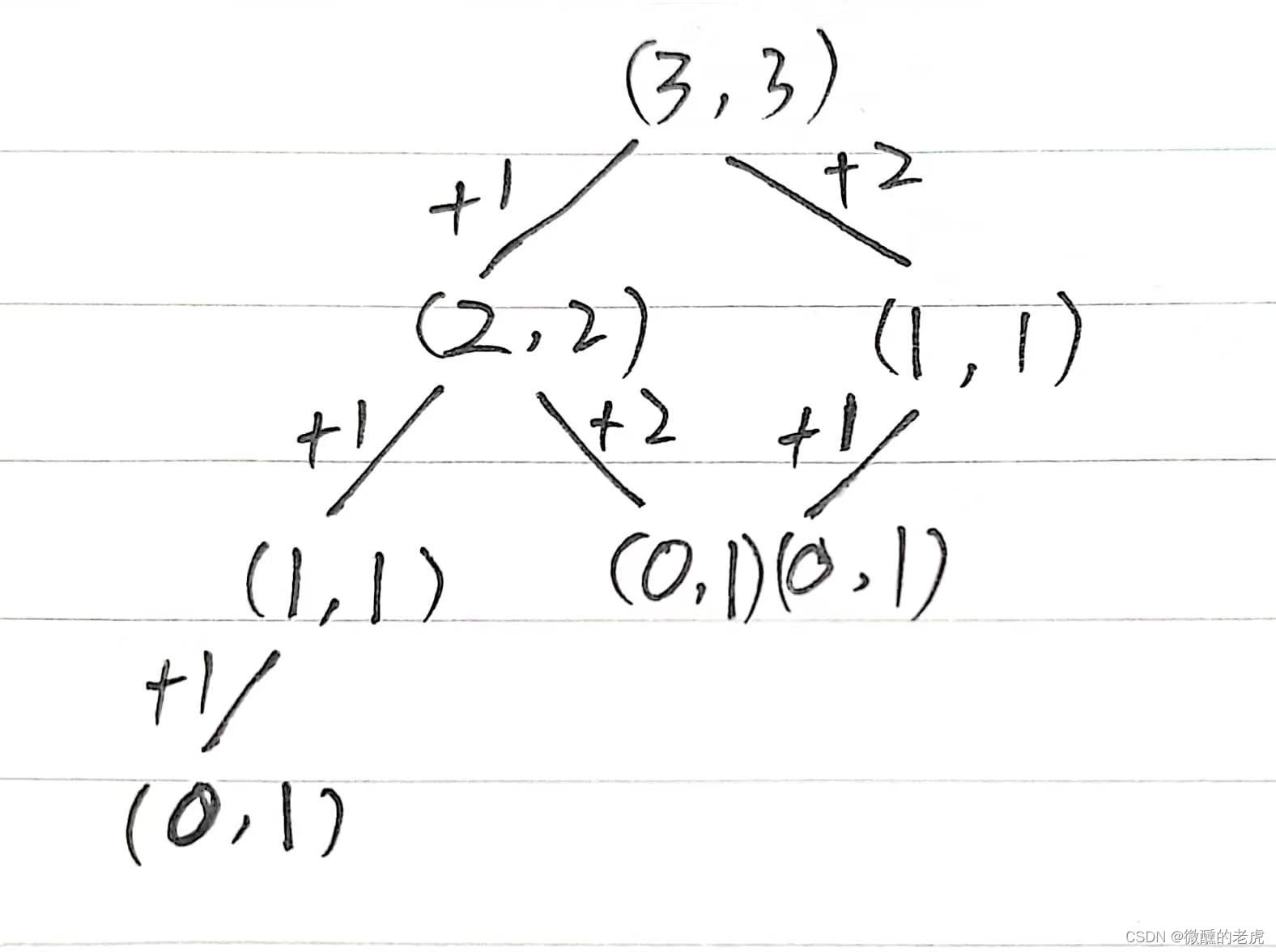
现在,用节点(0,1)表示之前的节点0,那么每个节点的含义就很明显了。第一个数表示在第0阶,第二个数表示到达第0阶的方法。显然的,一开始就在第0阶,那么到达第0阶的方法就1种。
节点(1,1)表示之前的节点1。到达第1阶的方法,只有从第0阶向上爬1阶,所以到达第1阶的方法就1种。
节点(2,2)表示之前的节点2。从图上看,到达第2阶有两种方法。第一种方法,先到达第1阶,然后再向上爬1阶。第二种方法,先到达第0阶,再向上爬2阶。所以,到达第2阶的方法=到达第1阶的方法+到达第0阶的方法。
同理,到达第3阶的方法=到达第2阶的方法+到达第1阶的方法。
第三步,确定搜索树节点连线的含义
很显然的,连线表示“向上爬的楼梯阶数”。每次可以选择向上爬1阶或2阶。
第四步,确定dp数组的含义。
从第二步确定节点的含义就可以看出,我们需要同时知道“所在的台阶”以及“到达该台阶的方法”才能解决问题。
用i来表示“所在的台阶”,i的范围为[0,n];用dp[i]来表示“到达第i阶的方法”。
第五步,列出递推公式。
从第二步可以看出,当i=0,1时,dp[i]=1;当i>1时,dp[i]=dp[i-1]+dp[i-2]。
所以递推公式如下
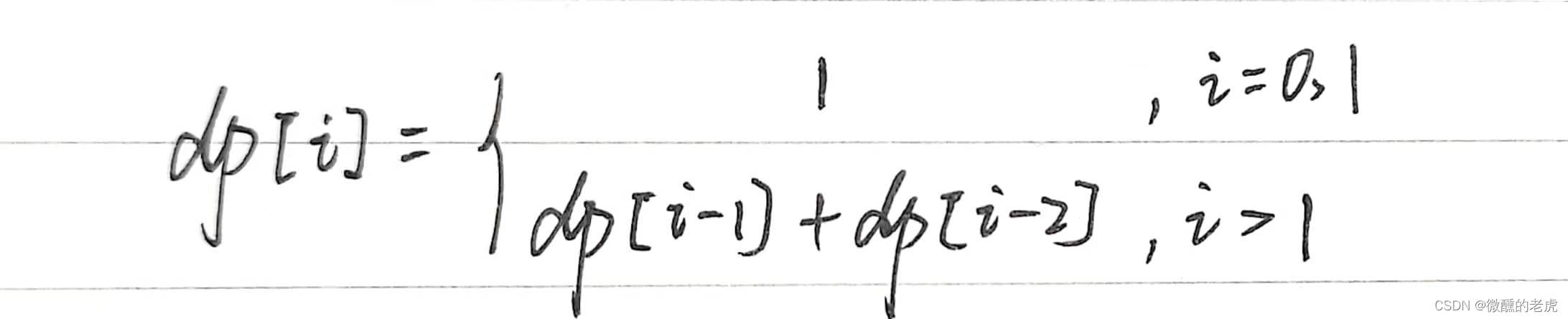
动态规划
经过上面的分析,最后我们得到了递推公式。现在,我们可以根据递推公式来填充dp数组。
class Solution {
public int climbStairs(int n) {
// 定义dp数组,i表示“所在的台阶”,dp[i]表示“到达第i阶的方法”。
int[] dp = new int[n + 1];
// 当i=0,1
dp[0] = 1;
dp[1] = 1;
// 当i>1
for(int i = 2; i <= n; i++){
dp[i] = dp[i - 1] + dp[i - 2];
}
// 返回“到达第n阶的方法”
return dp[n];
}
}
总结
我们用这道题,讲解了动态规划解题步骤。其中,最重要的就是画出搜索树,只要能够把搜索树画出来,然后把节点的含义和连线的含义搞清楚,就可以把节点转换成dp数组,把连线转换成递推公式。
下一题,将讲一下动态规划三要素。问题得先满足动态规划三要素,才能用动态规划的方法解题。
参考:
动态规划解题套路框架
算法设计与分析基础(第3版) (豆瓣)